7. Fehlende Daten & Ausreißer

Der Umgang mit fehlenden Daten und potenziellen Ausreißern

Author
Zugehörigkeit

Dr. Paul Schmidt

BioMath GmbH

Last updated

7. Februar 2026

Um alle in diesem Kapitel verwendeten Pakete zu installieren und zu laden, führe den folgenden Code aus:

for (pkg in c("broom", "here", "janitor", "naniar", "readxl", "tidyverse")) {
  if (!require(pkg, character.only = TRUE)) install.packages(pkg)
}

library(broom)
library(here)
library(janitor)
library(naniar)
library(readxl)
library(tidyverse)

Einführung

Bei der Datenanalyse in der realen Welt sind Datensätze selten in perfektem Zustand. Fehlende Werte, potenzielle Ausreißer und andere Datenqualitätsprobleme sind häufige Herausforderungen. Dieses Kapitel konzentriert sich darauf, wie man diese Probleme identifiziert und behandelt und wie sie statistische Analysen beeinflussen können.

Daten

In diesem Kapitel arbeiten wir mit einem Datensatz, der während eines hypothetischen Forschungsprojekts erhoben wurde, bei dem das Alter der Teilnehmer und ihre Sehqualität (auf einer Skala von 1-10) erfasst wurden. Die Daten wurden durch Befragung von 29 Personen auf einem Universitätscampus gesammelt.

Importieren

dat <- read_excel(here("data", "vision fixed.xls"))
head(dat, n = 5)
# A tibble: 5 × 9
  Person    Ages Gender Civil_state Height Profession  Vision Distance perc_dist
  <chr>    <dbl> <chr>  <chr>        <dbl> <chr>        <dbl>    <dbl>     <dbl>
1 Andrés      25 M      S              180 Student         10      1.5        15
2 Anja        29 F      S              168 Profession…     10      4.5        45
3 Armando     31 M      S              169 Profession…      9      4.5        50
4 Carlos      25 M      M              185 Profession…      8      6          75
5 Cristina    23 F      <NA>           170 Student         10      3          30

Es ist oft gute Praxis, Spaltennamen zu bereinigen, um sicherzustellen, dass sie konsistent und einfach zu verwenden sind. Man könnte die rename()-Funktion aus dem {dplyr}-Paket verwenden, aber das kann bei großen Datensätzen mit vielen Spalten mühsam sein. Stattdessen kann man die clean_names()-Funktion aus dem {janitor}-Paket verwenden, um Spaltennamen automatisch in ein konsistentes Format zu konvertieren (z.B. alles klein geschrieben, Unterstriche statt Leerzeichen):

dat <- dat %>% clean_names()
head(dat, n = 5)
# A tibble: 5 × 9
  person    ages gender civil_state height profession  vision distance perc_dist
  <chr>    <dbl> <chr>  <chr>        <dbl> <chr>        <dbl>    <dbl>     <dbl>
1 Andrés      25 M      S              180 Student         10      1.5        15
2 Anja        29 F      S              168 Profession…     10      4.5        45
3 Armando     31 M      S              169 Profession…      9      4.5        50
4 Carlos      25 M      M              185 Profession…      8      6          75
5 Cristina    23 F      <NA>           170 Student         10      3          30

Das ist das einzige Mal, dass wir das {janitor}-Paket in diesem Workshop verwenden werden, aber es ist ein sehr nützliches Paket zum Bereinigen unordentlicher Datensätze, also zögere nicht, seine anderen Funktionen zu erkunden.

Ziel

Ähnlich wie im vorherigen Kapitel über Korrelation und Regression ist unser Ziel, die Beziehung zwischen zwei numerischen Variablen zu analysieren: ages und vision. Dieser Datensatz stellt jedoch zwei zusätzliche Herausforderungen dar:

  1. Er enthält fehlende Werte
  2. Er scheint einen potenziellen Ausreißer zu haben

Erkunden

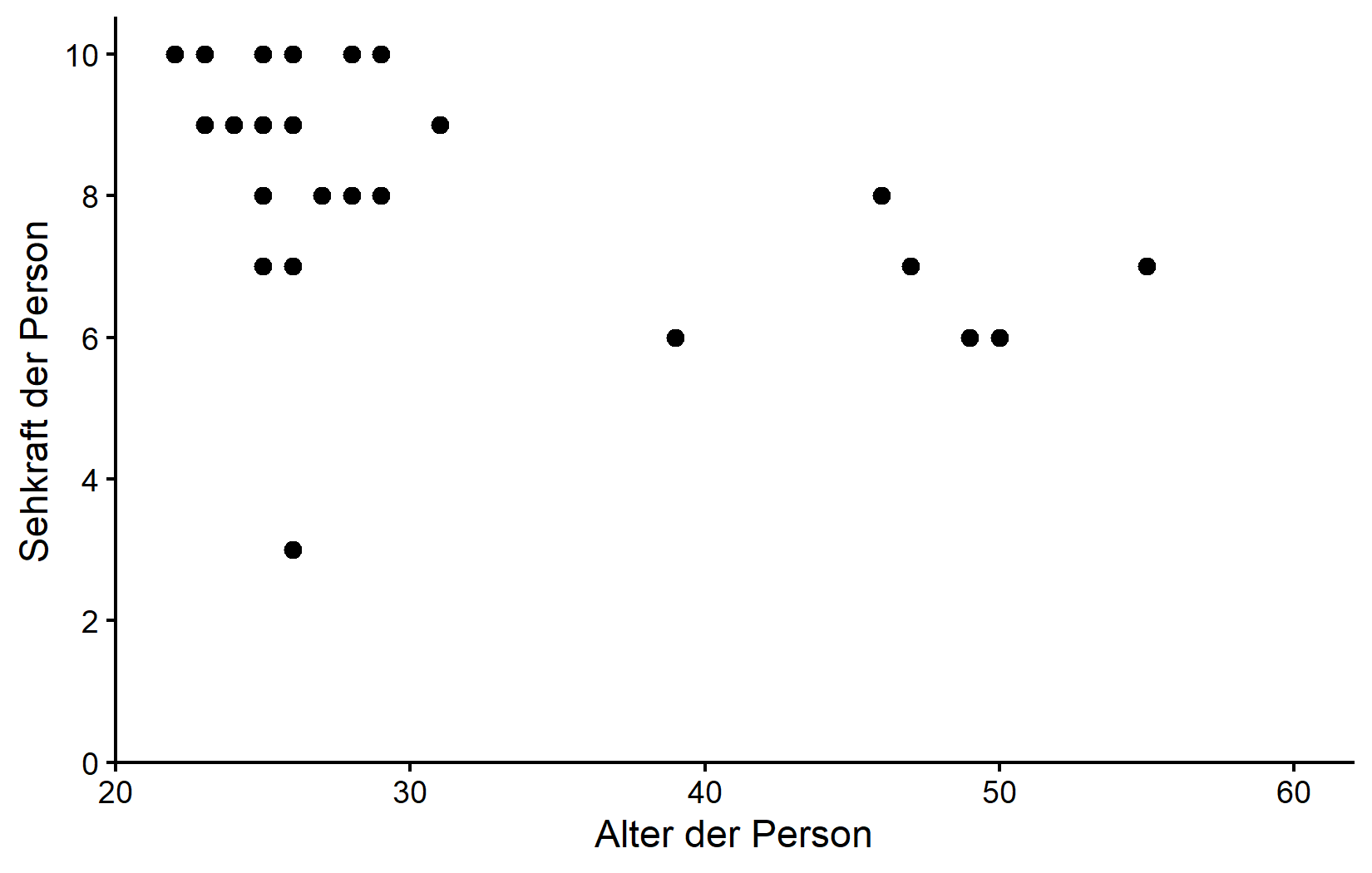
Beginnen wir mit einer Zusammenfassung unserer Daten und visualisieren die Beziehung zwischen Alter und Sehkraft:

summary(dat)
    person               ages          gender          civil_state       
 Length:29          Min.   :22.00   Length:29          Length:29         
 Class :character   1st Qu.:25.00   Class :character   Class :character  
 Mode  :character   Median :26.00   Mode  :character   Mode  :character  
                    Mean   :30.61                                        
                    3rd Qu.:29.50                                        
                    Max.   :55.00                                        
                    NA's   :1                                            
     height       profession            vision          distance    
 Min.   :145.0   Length:29          Min.   : 3.000   Min.   :1.500  
 1st Qu.:164.8   Class :character   1st Qu.: 7.000   1st Qu.:1.500  
 Median :168.0   Mode  :character   Median : 9.000   Median :3.000  
 Mean   :168.2                      Mean   : 8.357   Mean   :3.466  
 3rd Qu.:172.8                      3rd Qu.:10.000   3rd Qu.:4.500  
 Max.   :190.0                      Max.   :10.000   Max.   :6.000  
 NA's   :1                          NA's   :1                       
   perc_dist     
 Min.   : 15.00  
 1st Qu.: 20.24  
 Median : 40.18  
 Mean   : 45.45  
 3rd Qu.: 57.19  
 Max.   :150.00  
 NA's   :1       
ggplot(data = dat) +
  aes(x = ages, y = vision) +
  geom_point(size = 2) +
  scale_x_continuous(
    name = "Alter der Person",
    limits = c(20, 60),
    expand = expansion(mult = c(0, 0.05))
  ) +
  scale_y_continuous(
    name = "Sehkraft der Person",
    limits = c(0, NA),
    breaks = seq(0, 10, 2),
    expand = expansion(mult = c(0, 0.05))
  ) +
  theme_classic()
Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_point()`).

Die Visualisierung legt nahe, dass die meisten Teilnehmer in ihren Zwanzigern sind und relativ gute Sehwerte haben. Es scheint einen Trend zu geben, dass ältere Menschen tendenziell etwas schlechtere Sehkraft haben. Es gibt jedoch auch einen auffälligen potenziellen Ausreißer: jemand Mitte zwanzig mit einem Sehwert von nur 3, der erheblich niedriger ist als bei Gleichaltrigen.

Umgang mit fehlenden Daten

Obwohl der Datensatz 29 Zeilen enthält, haben wir nur vollständige Informationen über 28 Personen. Das liegt daran, dass es einen NA-Wert (Not Available) für die Sehkraft einer Person gibt.

Fehlende Werte identifizieren

In R werden fehlende Werte durch NA dargestellt und erfordern eine spezielle Behandlung. Um beispielsweise Zeilen mit fehlenden Werten zu filtern, kann man nicht == NA verwenden; stattdessen muss man die is.na()-Funktion verwenden:

dat %>%
  filter(is.na(vision))
# A tibble: 1 × 9
  person   ages gender civil_state height profession   vision distance perc_dist
  <chr>   <dbl> <chr>  <chr>        <dbl> <chr>         <dbl>    <dbl>     <dbl>
1 Enrique    NA <NA>   <NA>            NA Professional     NA        6        NA

Hier ist ein noch kleineres Beispiel dafür:

c(1, 2, 3, NA) == NA # funktioniert nicht richtig
[1] NA NA NA NA
c(1, 2, 3, NA) %>% is.na() # funktioniert
[1] FALSE FALSE FALSE  TRUE

Einige Funktionen reagieren empfindlich auf NAs

Einige Funktionen in R schließen fehlende Werte automatisch aus, andere nicht. Die mean()-Funktion gibt beispielsweise NA zurück, wenn einer der Werte fehlt:

c(1, 2, 3, NA) %>% mean()
[1] NA

Damit sie den fehlenden Wert ignoriert und den Mittelwert aller verbleibenden Werte berechnet, muss man das na.rm-Argument auf TRUE setzen:

c(1, 2, 3, NA) %>% mean(na.rm = TRUE)
[1] 2

Wenn wir das durchschnittliche Alter pro Beruf in unserem Datensatz berechnen wollten, müssten wir das na.rm-Argument auf TRUE setzen, um die fehlenden Werte zu ignorieren:

dat %>%
  group_by(profession) %>%
  summarise(
    mean_age = mean(ages)
  )
# A tibble: 2 × 2
  profession   mean_age
  <chr>           <dbl>
1 Professional     NA  
2 Student          24.4
dat %>%
  group_by(profession) %>%
  summarise(
    mean_age = mean(ages, na.rm = TRUE)
  )
# A tibble: 2 × 2
  profession   mean_age
  <chr>           <dbl>
1 Professional     34.6
2 Student          24.4

Beachte auch, dass wir beim Erstellen des ggplot oben eine Warnmeldung über fehlende Werte erhalten haben: “Warning: Removed 1 row containing missing values or values outside the scale range (geom_point()).” Das liegt daran, dass die geom_point()-Funktion automatisch alle Zeilen mit fehlenden Werten in den x- oder y-Ästhetiken ausschließt. Der Plot wurde trotzdem wie beabsichtigt erstellt, aber ggplot möchte sicherstellen, dass wir nicht übersehen, dass es einen fehlenden Wert in den Daten gab. Das ist eine gute Sache, da es uns hilft, potenzielle Probleme frühzeitig zu erkennen.

Fehlende Werte zählen

Um fehlende Werte in einem Datensatz zu zählen, ist der grundlegende Ansatz sum(is.na(column)) zu verwenden. Für nicht-fehlende Werte kann man sum(!is.na(column)) verwenden:

dat %>%
  group_by(profession) %>%
  summarise(
    n_rows = n(),
    n_missing = sum(is.na(vision)),
    n_complete = sum(!is.na(vision))
  )
# A tibble: 2 × 4
  profession   n_rows n_missing n_complete
  <chr>         <int>     <int>      <int>
1 Professional     18         1         17
2 Student          11         0         11

Das {naniar}-Paket bietet spezialisierte Funktionen für die Arbeit mit fehlenden Daten, die viel angenehmer zu verwenden sind:

dat %>%
  group_by(profession) %>%
  summarise(
    n_rows = n(),
    n_missing = n_miss(vision),
    n_complete = n_complete(vision)
  )
# A tibble: 2 × 4
  profession   n_rows n_missing n_complete
  <chr>         <int>     <int>      <int>
1 Professional     18         1         17
2 Student          11         0         11

Diese Ergebnisse zeigen, dass wir einen fehlenden Sehwert in der Berufskategorie “Student” haben. Wir haben diese eine Datenzeile bereits oben gesehen, als wir Enrique über filter(is.na(vision)) herausgefiltert haben. An diesem Punkt entfernen wir diese Zeile einfach aus unserem Datensatz, da sie ohnehin nicht zu unserer Analyse beitragen wird und wir so verhindern, dass die ggplot-Warnung jedes Mal auftaucht, wenn wir etwas plotten:

dat <- dat %>%
  filter(!is.na(vision)) # !is.na() ist das Gegenteil von is.na()

Anfängliche Korrelations- und Regressionsanalyse

Fahren wir mit unserer Korrelations- und Regressionsanalyse des Datensatzes fort, wie er ist (mit automatisch ausgeschlossenen fehlenden Werten).

cor <- cor.test(dat$vision, dat$ages)
tidy(cor)
# A tibble: 1 × 8
  estimate statistic p.value parameter conf.low conf.high method     alternative
     <dbl>     <dbl>   <dbl>     <int>    <dbl>     <dbl> <chr>      <chr>      
1   -0.497     -2.92 0.00709        26   -0.734    -0.153 Pearson's… two.sided  
reg <- lm(vision ~ ages, data = dat)
tidy(reg)
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)  11.1       0.996      11.2  1.97e-11
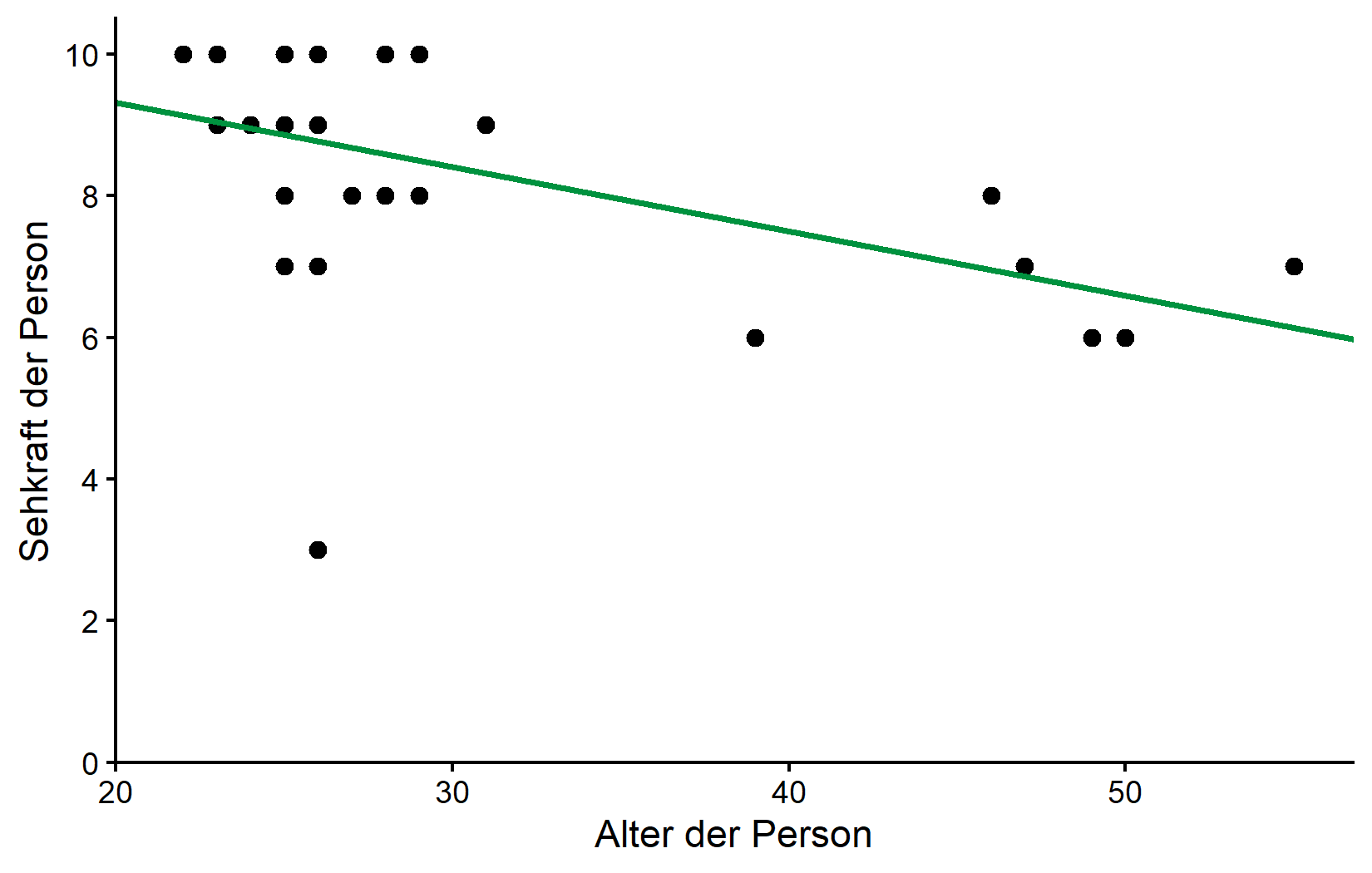
2 ages         -0.0910    0.0311     -2.92 7.09e- 3

Wir haben eine moderate negative Korrelation von ungefähr -0,5, die statistisch signifikant ist (p < 0,05). Die Regressionsgleichung lautet:

vision = 11.14 - 0.09 × ages

Visualisieren wir diese Beziehung mit unserer Regressionslinie:

ggplot(data = dat) +
  aes(x = ages, y = vision) +
  geom_point(size = 2) +
  geom_abline(
    intercept = reg$coefficients[1],
    slope = reg$coefficients[2],
    color = "#00923f",
    linewidth = 1
  ) +
  scale_x_continuous(
    name = "Alter der Person",
    limits = c(20, 55),
    expand = expansion(mult = c(0, 0.05))
  ) +
  scale_y_continuous(
    name = "Sehkraft der Person",
    limits = c(0, NA),
    breaks = seq(0, 10, 2),
    expand = expansion(mult = c(0, 0.05))
  ) +
  theme_classic()

Umgang mit Ausreißern

HinweisWeitere Quellen

Hier besprechen wir die manuelle und damit subjektive Identifikation eines Datenpunkts als potenziellen Ausreißer. Wir besprechen nicht automatische und damit objektive Ansätze zur Ausreißererkennung, aber siehe z.B. hier oder hier, wenn du dich dafür interessierst.

Wenn wir unseren Plot betrachten, scheint ein Datenpunkt herauszustechen: jemand Mitte zwanzig mit einem Sehwert von nur 3, der erheblich niedriger ist als bei allen anderen Teilnehmern ähnlichen Alters.

Schritt 1: Den potenziellen Ausreißer untersuchen

Wenn man einen potenziellen Ausreißer identifiziert, ist der erste Schritt, ihn näher zu untersuchen. Finden wir mehr über diesen Datenpunkt heraus:

dat %>%
  filter(vision == 3)
# A tibble: 1 × 9
  person   ages gender civil_state height profession   vision distance perc_dist
  <chr>   <dbl> <chr>  <chr>        <dbl> <chr>         <dbl>    <dbl>     <dbl>
1 Rolando    26 M      M              180 Professional      3      4.5       150

Wir stellen fest, dass der potenzielle Ausreißer ein 26-jähriger namens Rolando mit einem Sehwert von 3 ist.

Schritt 2: Eine informierte Entscheidung treffen

In der realen Forschung würde man an diesem Punkt:

  1. Die ursprünglichen Datensammlungsaufzeichnungen überprüfen, um zu bestätigen, dass dies kein Aufzeichnungsfehler war
  2. Das Wissen über den Teilnehmer (falls zutreffend) berücksichtigen, um zu bestimmen, ob es besondere Umstände gab
  3. Entscheiden, ob dieser Wert eine echte Beobachtung oder ein Fehler ist, der korrigiert oder entfernt werden sollte

Für dieses Beispiel nehmen wir an, dass wir uns entschieden haben, unsere Daten sowohl mit als auch ohne diesen potenziellen Ausreißer zu analysieren, um zu sehen, wie er unsere Ergebnisse beeinflusst.

Analyse ohne den Ausreißer

Erstellen wir einen neuen Datensatz ohne Rolando:

dat_no_outlier <- dat %>%
  filter(person != "Rolando")

Wiederholen wir nun unsere Korrelations- und Regressionsanalyse:

cor_no_outlier <- cor.test(dat_no_outlier$vision, dat_no_outlier$ages)
reg_no_outlier <- lm(vision ~ ages, data = dat_no_outlier)

Ergebnisse vergleichen

Vergleichen wir die Korrelationsergebnisse:

# Mit Ausreißer
tidy(cor) %>% select(1, 3, 5, 6)
# A tibble: 1 × 4
  estimate p.value conf.low conf.high
     <dbl>   <dbl>    <dbl>     <dbl>
1   -0.497 0.00709   -0.734    -0.153
# Ohne Ausreißer
tidy(cor_no_outlier) %>% select(1, 3, 5, 6)
# A tibble: 1 × 4
  estimate   p.value conf.low conf.high
     <dbl>     <dbl>    <dbl>     <dbl>
1   -0.696 0.0000548   -0.851    -0.430

Der Korrelationskoeffizient stieg von -0,5 auf -0,7, nachdem der Ausreißer entfernt wurde, was auf eine stärkere negative Beziehung zwischen Alter und Sehkraft hinweist. Das ist eine ziemlich drastische Veränderung, wenn man bedenkt, dass wir nur einen einzigen Datenpunkt entfernt haben.

Und die Regressionsergebnisse:

# Mit Ausreißer
tidy(reg) %>% select(1, 2, 3)
# A tibble: 2 × 3
  term        estimate std.error
  <chr>          <dbl>     <dbl>
1 (Intercept)  11.1       0.996 
2 ages         -0.0910    0.0311
# Ohne Ausreißer
tidy(reg_no_outlier) %>% select(1, 2, 3)
# A tibble: 2 × 3
  term        estimate std.error
  <chr>          <dbl>     <dbl>
1 (Intercept)   11.7      0.679 
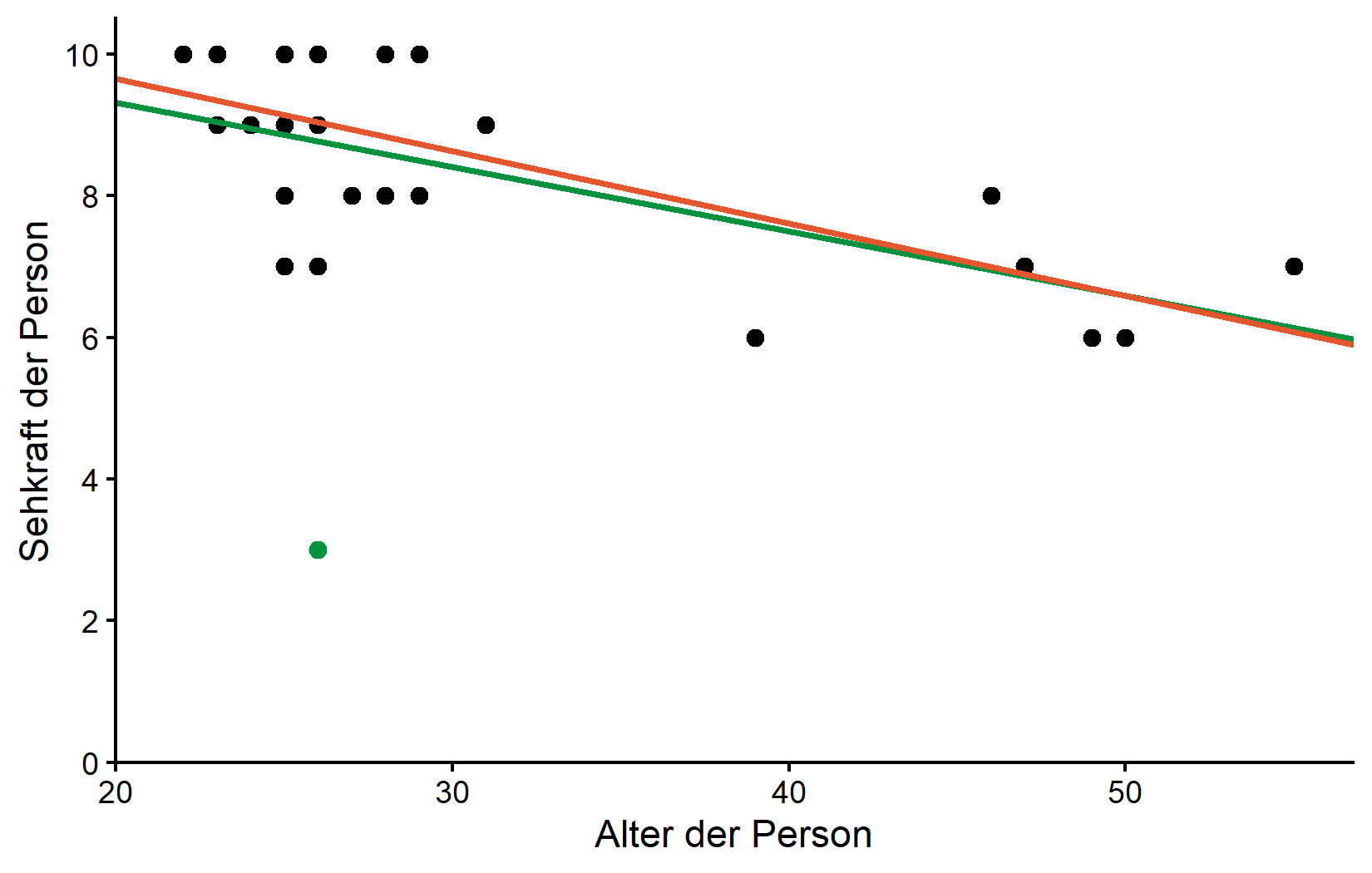
2 ages          -0.102    0.0211

Diese Werte haben sich eigentlich nicht so stark verändert, wie es scheint. Vor der Entfernung von Rolando war das geschätzte Modell vision = 11,1 - 0,0910*ages und nach seiner Entfernung ist es vision = 11,7 - 0,102*ages. Wir können auch die Regressionslinie ohne den Ausreißer (orange) Seite an Seite mit der Regressionslinie einschließlich des Ausreißers (grün) von vorher visualisieren:

ggplot() +
  aes(x = ages, y = vision) +
  # Alle Punkte von dat_no_outlier in Standardschwarz plotten
  geom_point(
    data = dat_no_outlier,
    size = 2
  ) +
  # Nur Rolando als grünen Punkt plotten
  geom_point(
    data = dat %>% filter(person == "Rolando"),
    color = "#00923f",
    size = 2
  ) +
  # Regressionslinie mit Ausreißer in grün plotten
  geom_abline(
    intercept = reg$coefficients[1],
    slope = reg$coefficients[2],
    color = "#00923f",
    linewidth = 1
  ) +
  # Regressionslinie ohne Ausreißer in orange plotten
  geom_abline(
    intercept = reg_no_outlier$coefficients[1],
    slope = reg_no_outlier$coefficients[2],
    color = "#e4572e",
    linewidth = 1
  ) +
  scale_x_continuous(
    name = "Alter der Person",
    limits = c(20, 55),
    expand = expansion(mult = c(0, 0.05))
  ) +
  scale_y_continuous(
    name = "Sehkraft der Person",
    limits = c(0, NA),
    breaks = seq(0, 10, 2),
    expand = expansion(mult = c(0, 0.05))
  ) +
  theme_classic()

Die Korrelationsschätzung hat sich also ziemlich verändert, aber die Regressionsschätzungen haben sich nicht so stark verändert. An diesem Punkt macht es jedoch Sinn zu fragen, wie gut jede angepasste Regressionslinie zu ihrem jeweiligen Datensatz passt:

Bestimmtheitsmaß

Eine nützliche Metrik zum Vergleich von Regressionsmodellen ist das Bestimmtheitsmaß (R²), das den Anteil der durch das Modell erklärten Varianz misst. Wir können diese Informationen aus unseren angepassten Regressionsmodellen (reg und reg_no_outlier) entweder über summary() oder wieder mit einer Funktion aus dem {broom}-Paket, d.h. glance(), erhalten:

# Mit Ausreißer
glance(reg) %>% select(contains("r.squared"))
# A tibble: 1 × 2
  r.squared adj.r.squared
      <dbl>         <dbl>
1     0.247         0.218
# Ohne Ausreißer
glance(reg_no_outlier) %>% select(contains("r.squared"))
# A tibble: 1 × 2
  r.squared adj.r.squared
      <dbl>         <dbl>
1     0.485         0.464

Obwohl sich die Regressionslinien (oder besser gesagt ihre Parameterschätzungen) möglicherweise nicht so stark verändert haben, hat sich die Erklärungskraft unseres Modells nach Entfernung des Ausreißers fast verdoppelt. Der R²-Wert stieg von 25% auf 49%, was darauf hinweist, dass das Modell ohne den Ausreißer einen viel größeren Anteil der Varianz in den Sehwerten erklärt. Mit anderen Worten: Die orange Linie erklärt alle Datenpunkte außer Rolando viel besser als die grüne Linie alle Datenpunkte einschließlich Rolando erklärt.

Zusammenfassung

Dieses Kapitel hat die Bedeutung einer sorgfältigen Untersuchung der Daten auf Qualitätsprobleme vor der Durchführung statistischer Analysen gezeigt. Wir haben gesehen, wie ein einziger Ausreißer die Korrelations- und Regressionsergebnisse erheblich beeinflussen kann.

WichtigWichtig
  1. Bewertung der Datenqualität:
    • Überprüfe immer auf fehlende Werte und potenzielle Ausreißer vor der Analyse
    • Verwende Funktionen wie is.na(), summary() und Visualisierung zur Identifikation von Problemen
  2. Umgang mit fehlenden Daten:
    • R schließt fehlende Werte (NA) normalerweise automatisch in Funktionen wie cor.test() und lm() aus
    • Pakete wie {naniar} bieten spezialisierte Tools für die Arbeit mit fehlenden Daten
    • Dokumentiere immer, wie viele Werte fehlten und wie sie behandelt wurden
  3. Umgang mit Ausreißern:
    • Untersuche potenzielle Ausreißer, um zu bestimmen, ob sie Fehler oder echte Beobachtungen darstellen
    • Erwäge, Daten sowohl mit als auch ohne Ausreißer zu analysieren, um ihre Auswirkung zu verstehen
    • Sei transparent über alle entfernten Datenpunkte und die Begründung
  4. Auswirkung auf statistische Analyse:
    • Die Entfernung von Rolando (unserem Ausreißer) veränderte die Korrelation von -0,5 auf -0,7
    • Der R²-Wert stieg von 25% auf 49% nach Entfernung des Ausreißers
    • Obwohl sich die Parameterschätzungen nicht dramatisch veränderten, verdoppelte sich fast die Erklärungskraft unseres Modells
  5. Bewährte Praktiken:
    • Entferne niemals Ausreißer nur, um deine Ergebnisse zu verbessern
    • Dokumentiere alle Datenbereinigungsentscheidungen
    • Erwäge, Ergebnisse sowohl mit als auch ohne Ausreißer zu berichten, wenn angemessen

Denke daran, dass statistische Tools zwar helfen können, potenzielle Probleme zu identifizieren, die Entscheidung, Datenpunkte einzuschließen oder auszuschließen, sollte jedoch auf soliden wissenschaftlichen Überlegungen beruhen und nicht auf statistischer Bequemlichkeit, wenn möglich. Sei immer transparent über deine Datenbehandlungsentscheidungen in jedem Forschungsbericht.

Zitat

Mit BibTeX zitieren:
@online{schmidt2026,
  author = {{Dr. Paul Schmidt}},
  publisher = {BioMath GmbH},
  title = {7. Fehlende Daten \& Ausreißer},
  date = {2026-02-07},
  url = {https://biomathcontent.netlify.app/de/content/r_intro/07_naoutlier.html},
  langid = {de}
}
Bitte zitieren Sie diese Arbeit als:
Dr. Paul Schmidt. 2026. “7. Fehlende Daten & Ausreißer.” BioMath GmbH. February 7, 2026. https://biomathcontent.netlify.app/de/content/r_intro/07_naoutlier.html.