# Pakete installieren (nur notwendig, falls noch nicht installiert)
for (pkg in c("broom", "ggrepel", "lubridate", "scales", "tidyverse")) {
if (!require(pkg, character.only = TRUE)) install.packages(pkg)
}
# Pakete laden
library(broom)
library(ggrepel)
library(lubridate)
library(scales)
library(tidyverse)Wer die Grundlagen der linearen Regression verstanden hat, steht oft vor der nächsten Frage: Wie bereite ich die Ergebnisse professionell auf? In Berichten und Publikationen sieht man häufig Streudiagramme, die weit über einen einfachen Punkteplot hinausgehen – mit Regressionsgerade, R²-Wert, Mittelwertlinien und beschrifteten Datenpunkten.
Dieses Kapitel zeigt Schritt für Schritt, wie solche Grafiken in R erstellt werden. Wir extrahieren die relevanten Kennzahlen aus dem Regressionsmodell und bauen daraus einen publikationsreifen Plot.
Pakete laden
Um alle in diesem Kapitel verwendeten Pakete zu installieren und zu laden, führt man folgenden Code aus:
Beispieldaten
Als Beispiel verwenden wir (synthetische) Regionaldaten zur Arbeitslosenquote in den 53 Kreisen und kreisfreien Städten Nordrhein-Westfalens.
set.seed(42)
# Echte Namen der 53 Kreise und kreisfreien Städte in NRW
kreis_namen <- c(
"Düsseldorf", "Duisburg", "Essen", "Krefeld", "Mönchengladbach",
"Mülheim an der Ruhr", "Oberhausen", "Remscheid", "Solingen", "Wuppertal",
"Kleve", "Mettmann", "Rhein-Kreis Neuss", "Viersen", "Wesel",
"Bonn", "Köln", "Leverkusen", "Städteregion Aachen", "Düren",
"Rhein-Erft-Kreis", "Euskirchen", "Heinsberg", "Oberbergischer Kreis",
"Rheinisch-Bergischer Kreis", "Rhein-Sieg-Kreis", "Bottrop", "Gelsenkirchen",
"Münster", "Borken", "Coesfeld", "Recklinghausen", "Steinfurt", "Warendorf",
"Bielefeld", "Gütersloh", "Herford", "Höxter", "Lippe", "Minden-Lübbecke",
"Paderborn", "Bochum", "Dortmund", "Hagen", "Hamm", "Herne",
"Ennepe-Ruhr-Kreis", "Märkischer Kreis", "Olpe", "Siegen-Wittgenstein",
"Soest", "Unna", "Hochsauerlandkreis"
)
n <- length(kreis_namen)
# Hilfsvektoren für differenzierte Quoten
staedte_hoch <- c("Gelsenkirchen", "Essen", "Duisburg", "Herne", "Dortmund")
kreise_niedrig <- c("Borken", "Coesfeld", "Höxter", "Olpe")
# Synthetische Daten mit realistischen Zusammenhängen
dat <- tibble(
kreis = kreis_namen,
# Basis-Zufallswerte
alo_quote = runif(n, 4, 9)
) %>%
mutate(
# Arbeitslosenquote: differenziert nach Kreistyp
alo_quote = case_when(
kreis %in% staedte_hoch ~ runif(n(), 10, 14),
kreis %in% kreise_niedrig ~ runif(n(), 2, 4),
TRUE ~ alo_quote
),
# Veränderung 2015-2023: korreliert positiv mit Quote
alo_veraenderung = -20 + 2.5 * alo_quote + rnorm(n(), 0, 8),
# Bruttolohn-Veränderung: 15-40%
bruttolohn_veraenderung = runif(n(), 15, 40),
# Bevölkerungsveränderung: korreliert negativ mit Lohnentwicklung
bevoelkerung_veraenderung = 5 - 0.3 * bruttolohn_veraenderung + rnorm(n(), 0, 3)
) %>%
arrange(kreis)
dat# A tibble: 53 × 5
kreis alo_quote alo_veraenderung bruttolohn_veraenderung
<chr> <dbl> <dbl> <dbl>
1 Bielefeld 4.02 -17.1 15.8
2 Bochum 6.18 -3.32 24.8
3 Bonn 8.70 -2.73 26.6
4 Borken 3.16 -15.1 23.3
5 Bottrop 5.95 -2.04 33.3
6 Coesfeld 3.64 -0.964 17.2
7 Dortmund 12.9 5.93 19.0
8 Duisburg 10.2 6.40 36.7
9 Düren 6.80 -12.7 23.2
10 Düsseldorf 8.57 5.18 18.4
# ℹ 43 more rows
# ℹ 1 more variable: bevoelkerung_veraenderung <dbl>Datenaufbereitung
Kategorien bilden mit cut()
Die Funktion cut() teilt eine kontinuierliche Variable in Kategorien auf. Das ist nützlich, um z.B. Quoten in Gruppen wie “niedrig”, “mittel”, “hoch” einzuteilen.
dat <- dat %>%
mutate(
quote_kategorie = cut(
alo_quote,
breaks = c(0, 4, 7, 10, Inf),
labels = c("niedrig (<4%)", "mittel (4-7%)", "erhöht (7-10%)", "hoch (>10%)"),
right = FALSE
)
)
# Verteilung der Kategorien
dat %>%
count(quote_kategorie)# A tibble: 4 × 2
quote_kategorie n
<fct> <int>
1 niedrig (<4%) 4
2 mittel (4-7%) 22
3 erhöht (7-10%) 22
4 hoch (>10%) 5Der Parameter right = FALSE bedeutet, dass die Intervalle links geschlossen sind: [0, 4) enthält 0, aber nicht 4. Mit labels vergeben wir aussagekräftige Namen für die Kategorien.
Datumsdifferenzen mit lubridate
Für Analysen über Zeiträume müssen häufig Differenzen zwischen Datumsangaben berechnet werden. Das Paket lubridate macht dies einfach.
# Beispiel: Beobachtungszeitraum
dat <- dat %>%
mutate(
datum_start = ymd("2015-01-01"),
datum_ende = ymd("2023-12-31"),
# Differenz in Tagen
tage = as.numeric(datum_ende - datum_start),
# Differenz in Jahren (exakt)
jahre = interval(datum_start, datum_ende) / years(1)
)
# Ergebnis prüfen
dat %>%
select(kreis, datum_start, datum_ende, tage, jahre) %>%
head(3)# A tibble: 3 × 5
kreis datum_start datum_ende tage jahre
<chr> <date> <date> <dbl> <dbl>
1 Bielefeld 2015-01-01 2023-12-31 3286 9.00
2 Bochum 2015-01-01 2023-12-31 3286 9.00
3 Bonn 2015-01-01 2023-12-31 3286 9.00Die Funktion interval() erzeugt ein Zeitintervall, das wir dann durch years(1) teilen, um die exakte Anzahl der Jahre zu erhalten. Für einfache Differenzen in Tagen reicht die Subtraktion mit anschließender Umwandlung via as.numeric().
Lineare Regression
Bevor wir die Daten visualisieren, passen wir das Regressionsmodell an. Die Ergebnisse – insbesondere Steigung, Achsenabschnitt und R² – benötigen wir später für den Plot.
Modell anpassen
# Einfache lineare Regression:
# Wie hängt die Veränderung der Quote mit der aktuellen Höhe zusammen?
mod <- lm(alo_veraenderung ~ alo_quote, data = dat)
# Zusammenfassung
summary(mod)
Call:
lm(formula = alo_veraenderung ~ alo_quote, data = dat)
Residuals:
Min 1Q Median 3Q Max
-16.378 -6.249 0.163 5.930 14.790
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -20.2319 3.2374 -6.249 8.32e-08 ***
alo_quote 2.4302 0.4329 5.614 8.19e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.31 on 51 degrees of freedom
Multiple R-squared: 0.382, Adjusted R-squared: 0.3698
F-statistic: 31.52 on 1 and 51 DF, p-value: 8.194e-07Ergebnisse extrahieren mit broom
Das Paket broom bietet drei zentrale Funktionen, um Modellausgaben in ordentliche Tibbles zu überführen:
# Koeffizienten mit Standardfehlern und p-Werten
tidy(mod)# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -20.2 3.24 -6.25 0.0000000832
2 alo_quote 2.43 0.433 5.61 0.000000819 # Modellgüte: R², adjustiertes R², F-Statistik, etc.
glance(mod)# A tibble: 1 × 12
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.382 0.370 7.31 31.5 0.000000819 1 -180. 365. 371.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int># Vorhersagewerte und Residuen für jede Beobachtung
augment(mod) %>%
head()# A tibble: 6 × 8
alo_veraenderung alo_quote .fitted .resid .hat .sigma .cooksd .std.resid
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 -17.1 4.02 -10.5 -6.65 0.0524 7.32 0.0241 -0.934
2 -3.32 6.18 -5.22 1.90 0.0219 7.38 0.000774 0.263
3 -2.73 8.70 0.911 -3.64 0.0277 7.36 0.00364 -0.505
4 -15.1 3.16 -12.6 -2.56 0.0736 7.37 0.00525 -0.364
5 -2.04 5.95 -5.77 3.73 0.0236 7.36 0.00321 0.516
6 -0.964 3.64 -11.4 10.4 0.0610 7.22 0.0703 1.47 Werte für die Visualisierung speichern
Für den Plot benötigen wir den Achsenabschnitt, die Steigung und das R²:
# Achsenabschnitt und Steigung für geom_abline()
intercept <- coef(mod)[1]
slope <- coef(mod)[2]
# R² für die Annotation
r_squared <- glance(mod)$r.squared
# Werte ausgeben
glue::glue("Achsenabschnitt (a): {scales::number(intercept, accuracy = 0.01, decimal.mark = ',')}")Achsenabschnitt (a): -20,23glue::glue("Steigung (b): {scales::number(slope, accuracy = 0.001, decimal.mark = ',')}")Steigung (b): 2,430glue::glue("R²: {scales::number(r_squared, accuracy = 0.001, decimal.mark = ',')}")R²: 0,382Vorhersagewerte berechnen
Mit predict() können wir Vorhersagen für beliebige x-Werte erhalten:
# Vorhersage für bestimmte Arbeitslosenquoten
neue_werte <- tibble(alo_quote = c(3, 6, 9, 12))
neue_werte %>%
mutate(
vorhergesagt = predict(mod, newdata = neue_werte)
)# A tibble: 4 × 2
alo_quote vorhergesagt
<dbl> <dbl>
1 3 -12.9
2 6 -5.65
3 9 1.64
4 12 8.93Alternativ fügt augment() die Vorhersagewerte direkt an den Originaldatensatz an (Spalte .fitted).
Annotierte Streudiagramme
Nun erstellen wir Schritt für Schritt einen publikationsreifen Plot mit allen relevanten Annotationen.
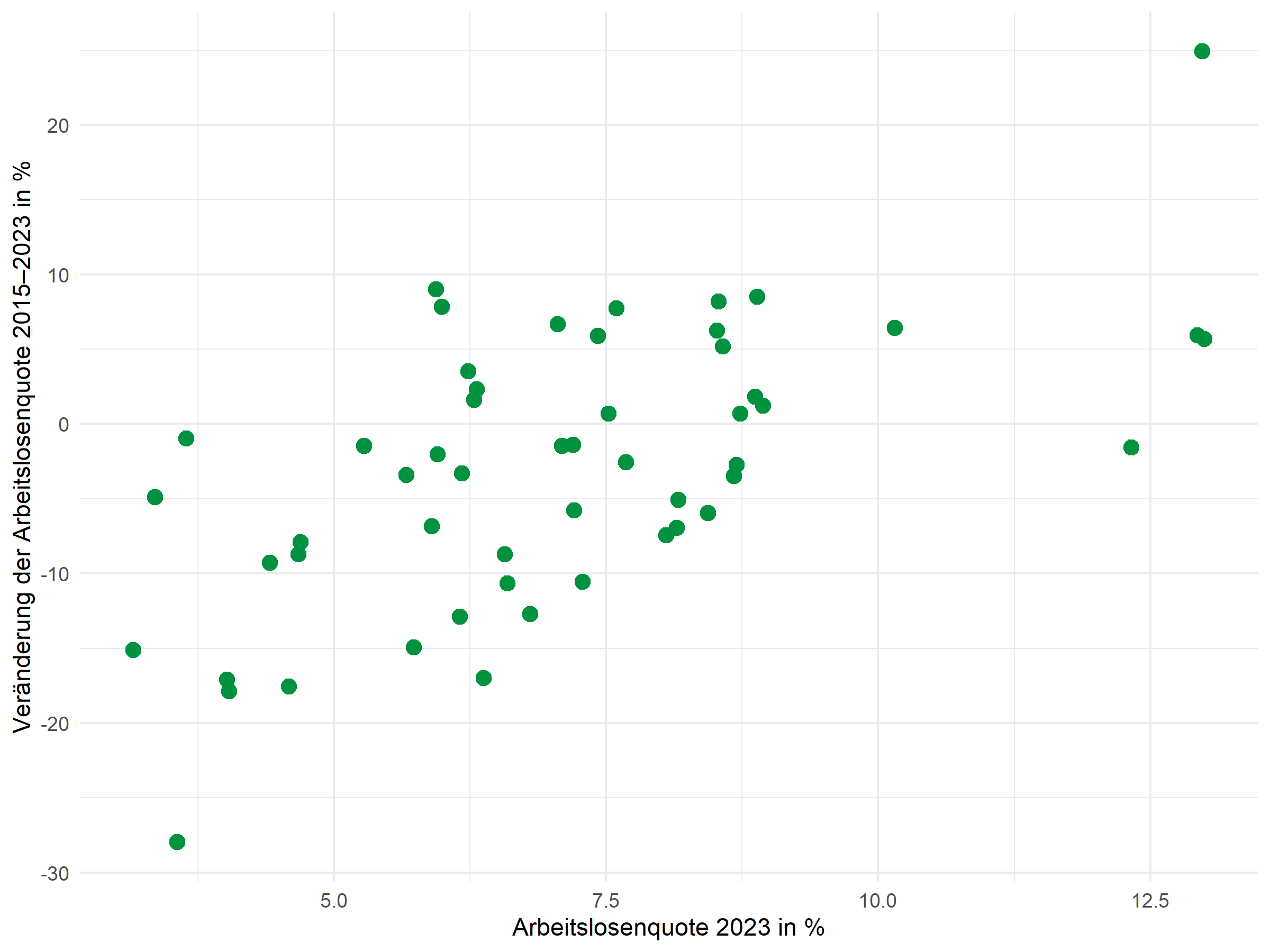
Basis-Streudiagramm
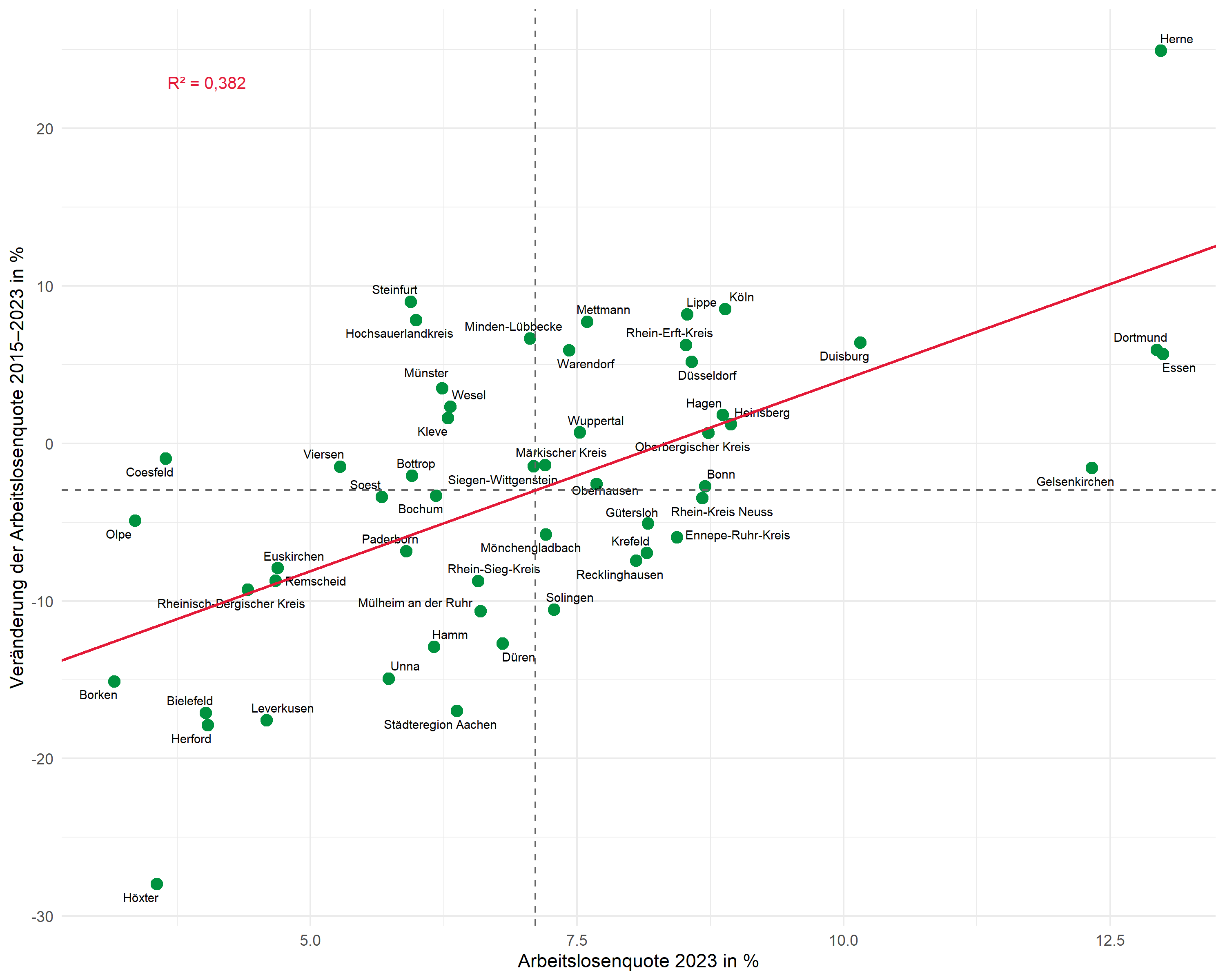
Der Grundplot zeigt die Beziehung zwischen der Arbeitslosenquote (x-Achse) und deren Veränderung über die Zeit (y-Achse):
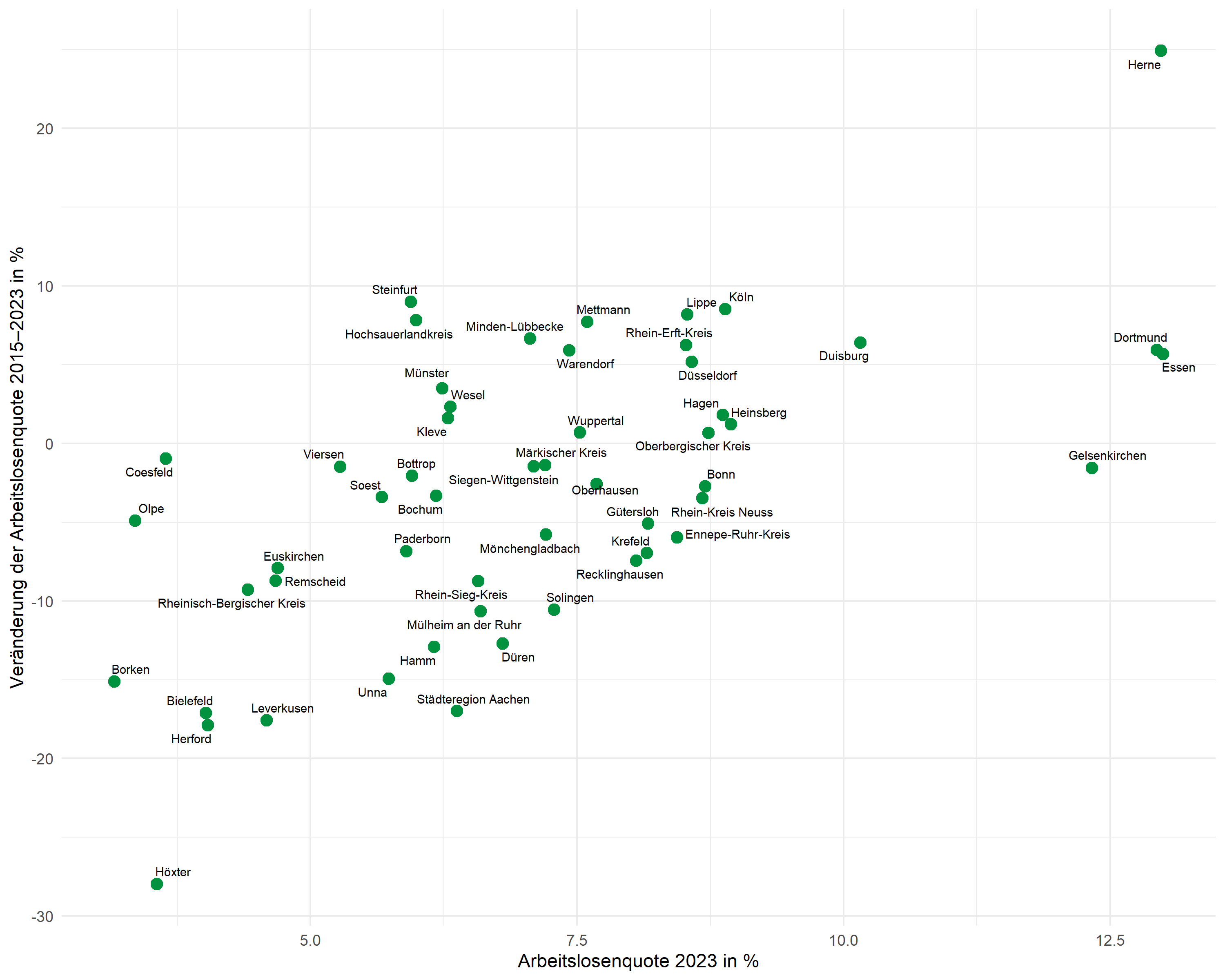
Punktbeschriftungen mit ggrepel
Das Paket ggrepel positioniert Beschriftungen automatisch so, dass sie sich nicht überlappen:
p <- p +
geom_text_repel(
aes(label = kreis),
size = 2.5,
max.overlaps = 20,
segment.color = "grey50",
segment.size = 0.3
)
pDer Parameter max.overlaps steuert, wie viele Überlappungen toleriert werden – bei vielen Punkten muss dieser Wert erhöht werden, damit alle Beschriftungen angezeigt werden.
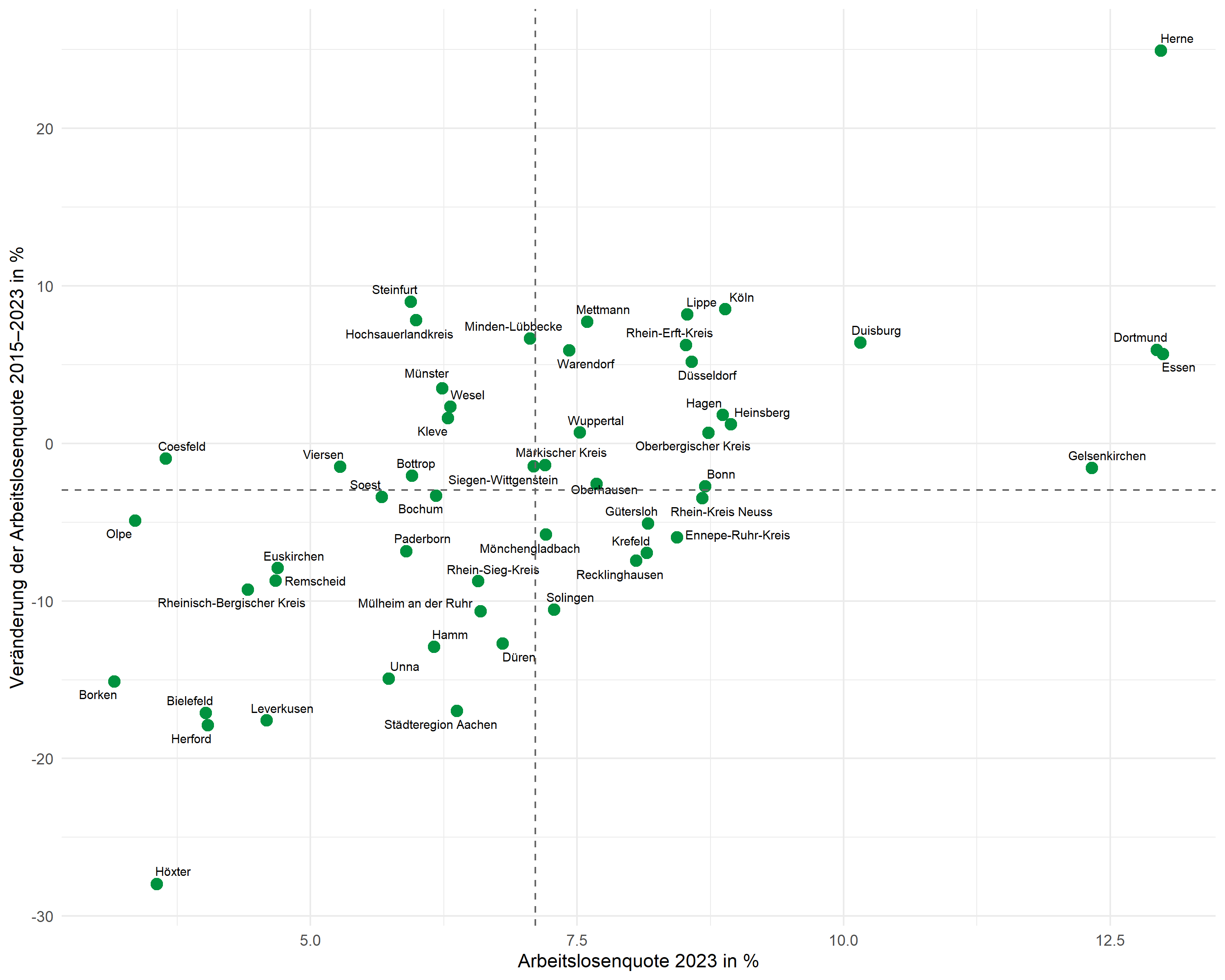
Mittelwertlinien
Gestrichelte Linien markieren die Mittelwerte beider Variablen und teilen den Plot in vier Quadranten:
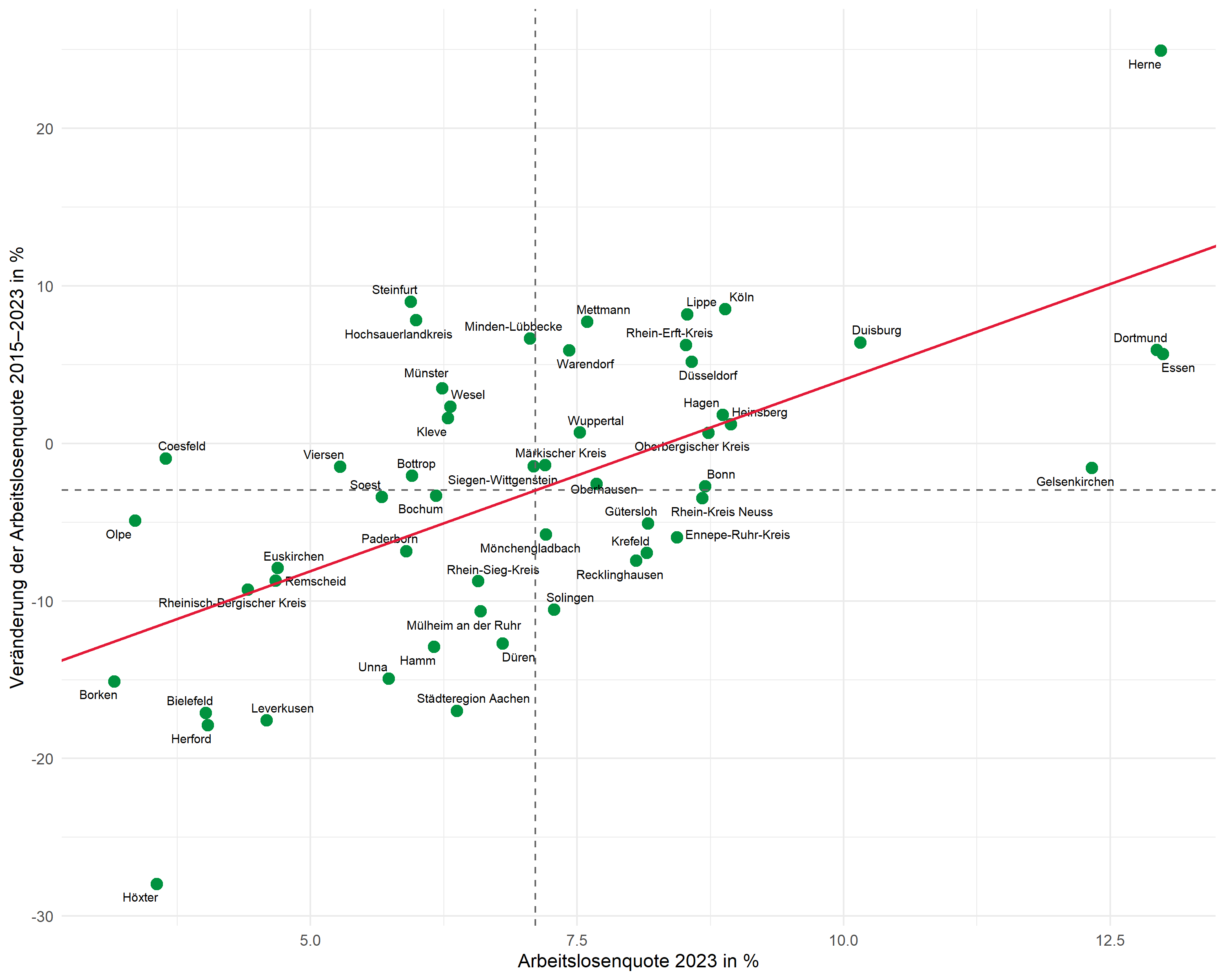
Regressionsgerade
Anstatt geom_smooth() verwenden wir geom_abline() mit den zuvor extrahierten Koeffizienten. So haben wir volle Kontrolle über die dargestellte Gerade:
R2-Annotation
Die R²-Annotation platzieren wir mit annotate(). Die Position wählen wir manuell, passend zum Datenbereich:
# R² formatiert mit deutschem Dezimaltrennzeichen
r2_label <- glue::glue("R² = {scales::number(r_squared, accuracy = 0.001, decimal.mark = ',')}")
p <- p +
annotate(
"text",
x = min(dat$alo_quote) + 0.5,
y = max(dat$alo_veraenderung) - 2,
label = r2_label,
hjust = 0,
size = 3.5,
color = "#E31937"
)
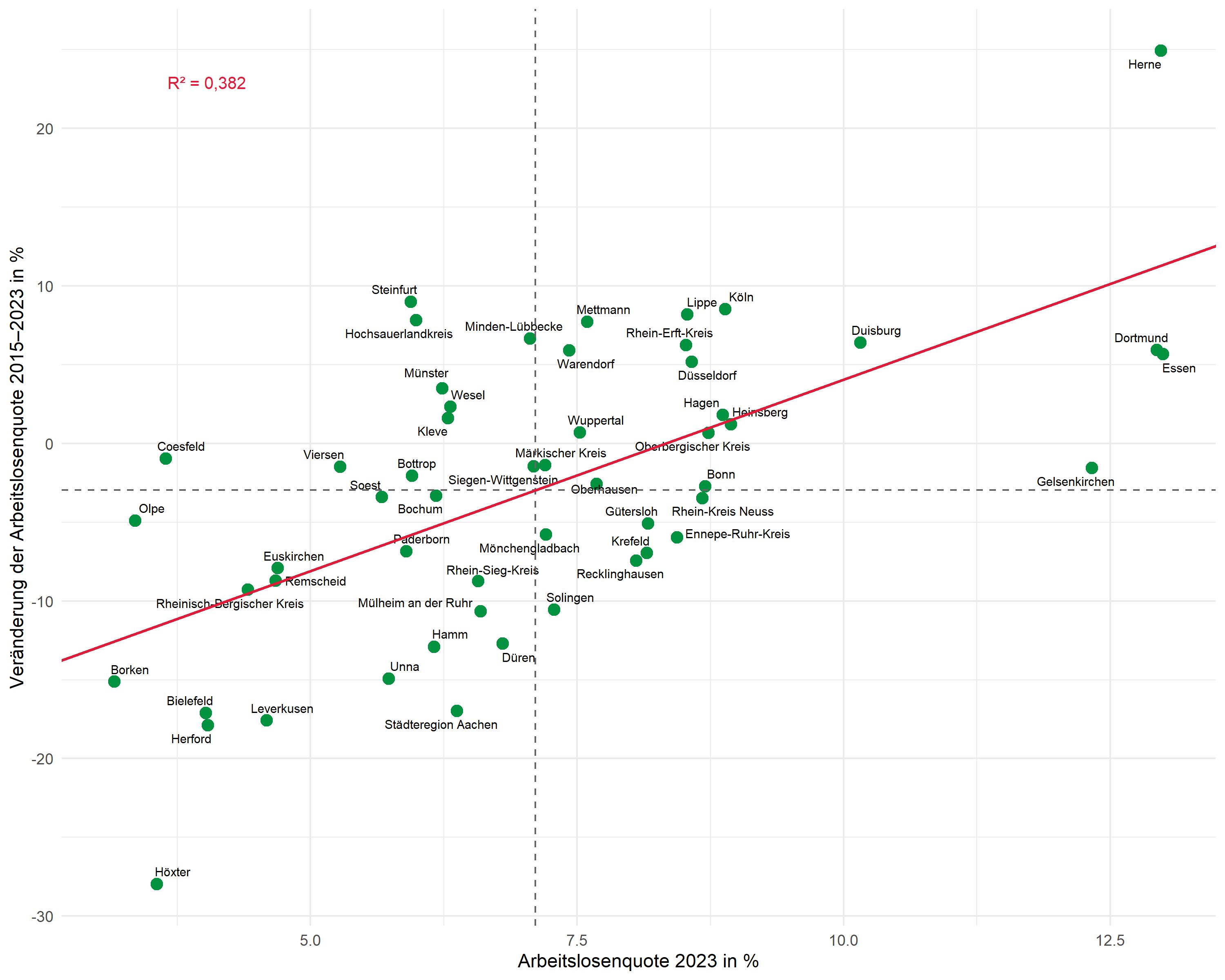
pVollständiger Plot
Hier der komplette Code für den fertigen Plot:
# Mittelwerte und Regressionsparameter
mean_x <- mean(dat$alo_quote)
mean_y <- mean(dat$alo_veraenderung)
r2_label <- glue::glue("R² = {scales::number(r_squared, accuracy = 0.001, decimal.mark = ',')}")
ggplot(dat, aes(x = alo_quote, y = alo_veraenderung)) +
# Punkte
geom_point(color = "#00923f", size = 3) +
# Beschriftungen
geom_text_repel(
aes(label = kreis),
size = 2.5,
max.overlaps = 25,
segment.color = "grey50",
segment.size = 0.3
) +
# Mittelwertlinien
geom_hline(yintercept = mean_y, linetype = "dashed", color = "grey40") +
geom_vline(xintercept = mean_x, linetype = "dashed", color = "grey40") +
# Regressionsgerade
geom_abline(
intercept = intercept,
slope = slope,
color = "#E31937",
linewidth = 0.8
) +
# R²-Annotation
annotate(
"text",
x = min(dat$alo_quote) + 0.5,
y = max(dat$alo_veraenderung) - 2,
label = r2_label,
hjust = 0,
size = 3.5,
color = "#E31937"
) +
# Achsenbeschriftungen
labs(
x = "Arbeitslosenquote 2023 in %",
y = "Veränderung der Arbeitslosenquote 2015–2023 in %"
) +
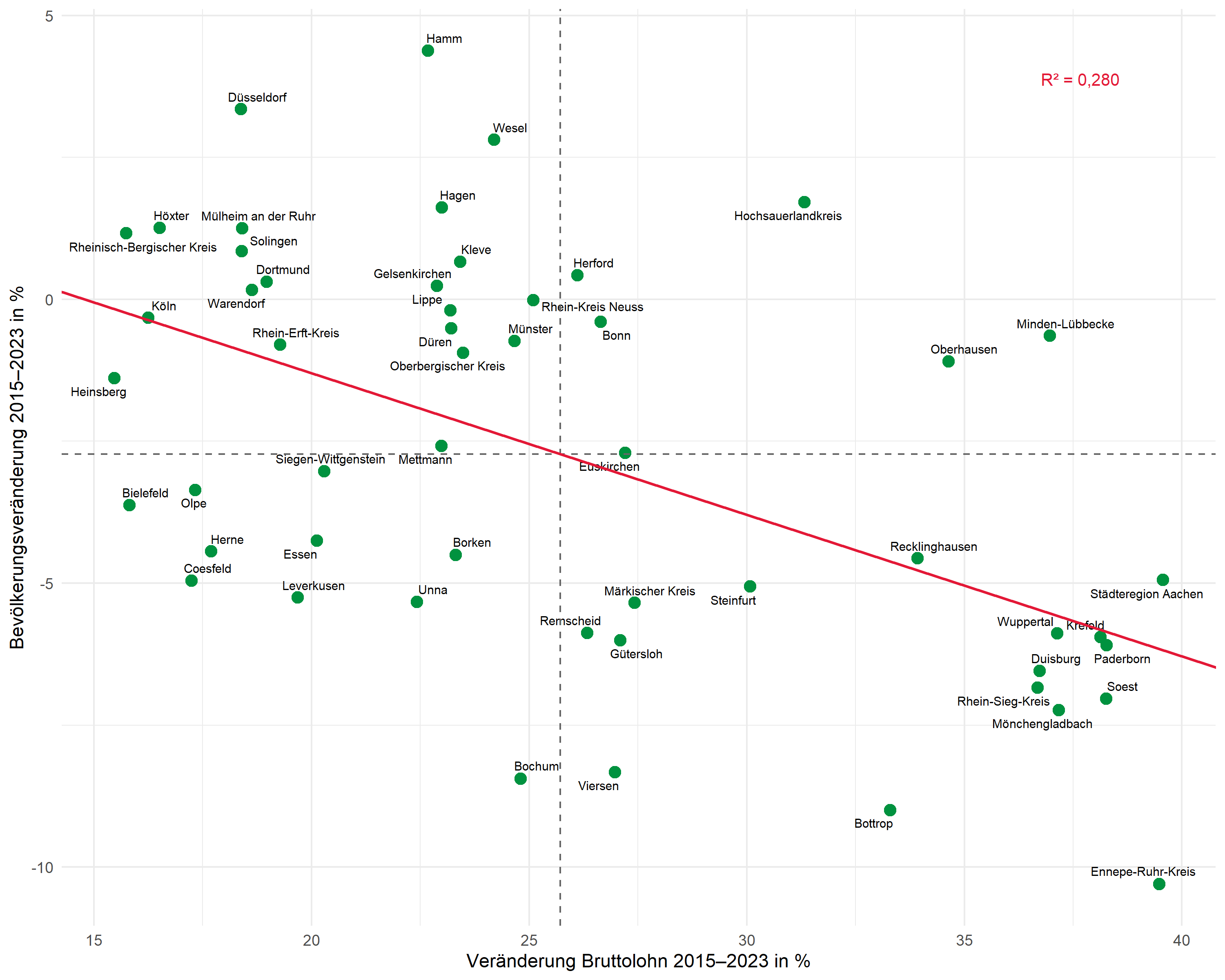
theme_minimal(base_size = 11)Zweites Beispiel: Lohnentwicklung und Bevölkerung
Der gleiche Workflow lässt sich auf andere Fragestellungen anwenden. Hier untersuchen wir den Zusammenhang zwischen der Bruttolohnentwicklung und der Bevölkerungsveränderung:
# Regression anpassen
mod2 <- lm(bevoelkerung_veraenderung ~ bruttolohn_veraenderung, data = dat)
# Werte extrahieren
intercept2 <- coef(mod2)[1]
slope2 <- coef(mod2)[2]
r_squared2 <- glance(mod2)$r.squared
r2_label2 <- glue::glue("R² = {scales::number(r_squared2, accuracy = 0.001, decimal.mark = ',')}")
# Plot
ggplot(dat, aes(x = bruttolohn_veraenderung, y = bevoelkerung_veraenderung)) +
geom_point(color = "#00923f", size = 3) +
geom_text_repel(
aes(label = kreis),
size = 2.5,
max.overlaps = 25,
segment.color = "grey50"
) +
geom_hline(yintercept = mean(dat$bevoelkerung_veraenderung), linetype = "dashed", color = "grey40") +
geom_vline(xintercept = mean(dat$bruttolohn_veraenderung), linetype = "dashed", color = "grey40") +
geom_abline(intercept = intercept2, slope = slope2, color = "#E31937", linewidth = 0.8) +
annotate(
"text",
x = max(dat$bruttolohn_veraenderung) - 1,
y = max(dat$bevoelkerung_veraenderung) - 0.5,
label = r2_label2,
hjust = 1,
size = 3.5,
color = "#E31937"
) +
labs(
x = "Veränderung Bruttolohn 2015–2023 in %",
y = "Bevölkerungsveränderung 2015–2023 in %"
) +
theme_minimal(base_size = 11)Bonus: Erweiterter Plot
In diesem Abschnitt erweitern wir den Plot um zusätzliche Elemente:
- Regressionsgleichung als Annotation (in der Form y = a + bx)
- Mittelwerte beschriftet an den gestrichelten Linien
- Selektives Labeln – nur die extremsten Werte werden beschriftet
Regressionsgleichung erstellen
Die Regressionsgleichung bauen wir aus den extrahierten Koeffizienten zusammen:
# Koeffizienten formatieren
a_fmt <- scales::number(intercept, accuracy = 0.01, decimal.mark = ",")
b_fmt <- scales::number(slope, accuracy = 0.01, decimal.mark = ",")
# Vorzeichen für b berücksichtigen
vorzeichen <- if_else(slope >= 0, " + ", " − ")
b_abs <- scales::number(abs(slope), accuracy = 0.01, decimal.mark = ",")
# Regressionsgleichung zusammenbauen
formel_label <- glue::glue("y = {a_fmt}{vorzeichen}{b_abs}x")
formel_labely = -20,23 + 2,43xSelektives Labeln vorbereiten
Bei vielen Datenpunkten kann es sinnvoll sein, nur die extremsten Werte zu beschriften. Hier labeln wir alle Punkte, die auf mindestens einer Achse zu den fünf höchsten oder fünf niedrigsten gehören:
dat <- dat %>%
mutate(
# Ränge berechnen (1 = niedrigster Wert)
rang_x = rank(alo_quote),
rang_y = rank(alo_veraenderung),
# Label für Extremwerte auf beiden Achsen
label_selektiv = if_else(
rang_x <= 5 | rang_x > n() - 5 | rang_y <= 5 | rang_y > n() - 5,
kreis,
NA_character_
)
)
# Prüfen, welche Kreise gelabelt werden
dat %>%
filter(!is.na(label_selektiv)) %>%
select(kreis, alo_quote, rang_x, alo_veraenderung, rang_y)# A tibble: 17 × 5
kreis alo_quote rang_x alo_veraenderung rang_y
<chr> <dbl> <dbl> <dbl> <dbl>
1 Bielefeld 4.02 5 -17.1 4
2 Borken 3.16 1 -15.1 6
3 Coesfeld 3.64 4 -0.964 33
4 Dortmund 12.9 51 5.93 44
5 Duisburg 10.2 49 6.40 46
6 Essen 13.0 53 5.67 42
7 Gelsenkirchen 12.3 50 -1.56 29
8 Herford 4.04 6 -17.9 2
9 Herne 13.0 52 24.9 53
10 Hochsauerlandkreis 5.99 17 7.82 49
11 Höxter 3.56 3 -28.0 1
12 Köln 8.89 47 8.52 51
13 Leverkusen 4.59 8 -17.6 3
14 Lippe 8.53 41 8.19 50
15 Olpe 3.36 2 -4.91 22
16 Steinfurt 5.94 15 9.00 52
17 Städteregion Aachen 6.37 23 -17.0 5Erweiterter Plot
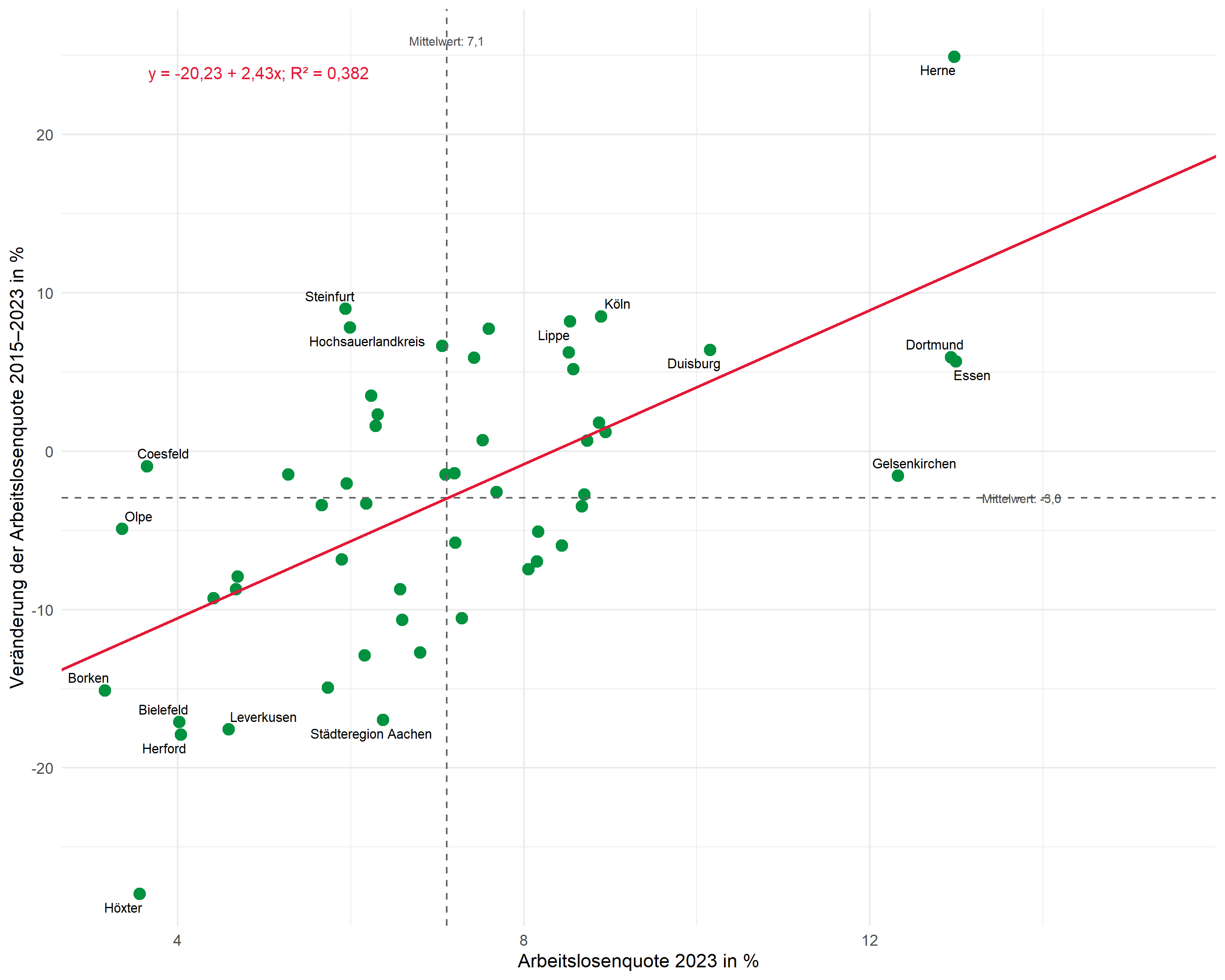
Nun kombinieren wir alle Elemente:
# Mittelwerte berechnen
mean_x <- mean(dat$alo_quote)
mean_y <- mean(dat$alo_veraenderung)
# Labels für Mittelwerte
mean_x_label <- glue::glue("Mittelwert: {scales::number(mean_x, accuracy = 0.1, decimal.mark = ',')}")
mean_y_label <- glue::glue("Mittelwert: {scales::number(mean_y, accuracy = 0.1, decimal.mark = ',')}")
# R² und Formel kombiniert
reg_label <- glue::glue("{formel_label}; R² = {scales::number(r_squared, accuracy = 0.001, decimal.mark = ',')}")
ggplot(dat, aes(x = alo_quote, y = alo_veraenderung)) +
# Punkte
geom_point(color = "#00923f", size = 3) +
# Selektive Beschriftungen (nur Extremwerte)
geom_text_repel(
aes(label = label_selektiv),
size = 2.8,
max.overlaps = 20,
segment.color = "grey50",
segment.size = 0.3,
na.rm = TRUE
) +
# Mittelwertlinien
geom_hline(yintercept = mean_y, linetype = "dashed", color = "grey40") +
geom_vline(xintercept = mean_x, linetype = "dashed", color = "grey40") +
# Mittelwert-Beschriftung (x-Achse, am oberen Rand)
annotate(
"text",
x = mean_x,
y = max(dat$alo_veraenderung) + 1,
label = mean_x_label,
size = 2.5,
color = "grey30"
) +
# Mittelwert-Beschriftung (y-Achse, am rechten Rand)
annotate(
"text",
x = max(dat$alo_quote) + 0.3,
y = mean_y,
label = mean_y_label,
hjust = 0,
size = 2.5,
color = "grey30"
) +
# Regressionsgerade
geom_abline(
intercept = intercept,
slope = slope,
color = "#E31937",
linewidth = 0.8
) +
# R² und Regressionsgleichung kombiniert
annotate(
"text",
x = min(dat$alo_quote) + 0.5,
y = max(dat$alo_veraenderung) - 1,
label = reg_label,
hjust = 0,
size = 3.5,
color = "#E31937"
) +
# Achsen mit scale_x/y_continuous
scale_x_continuous(
name = "Arbeitslosenquote 2023 in %",
limits = c(min(dat$alo_quote) - 0.5, max(dat$alo_quote) + 3),
expand = c(0, 0)
) +
scale_y_continuous(
name = "Veränderung der Arbeitslosenquote 2015–2023 in %",
limits = c(min(dat$alo_veraenderung) - 2, max(dat$alo_veraenderung) + 3),
expand = c(0, 0)
) +
theme_minimal(base_size = 11)Dieser erweiterte Plot zeigt:
- Selektives Labeln: Nur die Extremwerte auf beiden Achsen (jeweils Top/Bottom 5) sind beschriftet – der Rest bleibt übersichtlich
- Mittelwerte beschriftet: Die durchschnittlichen Werte stehen direkt an den gestrichelten Linien
- Regressionsgleichung und R²: Beide Informationen kompakt in einer Annotation
Zusammenfassung
Der Workflow für professionell aufbereitete Regressionsplots:
-
Modell anpassen:
lm()für die Regression -
Werte extrahieren:
broom-Funktionen liefern Koeffizienten, R² und Vorhersagewerte als Tibbles -
Plot schrittweise aufbauen:
-
geom_point()für die Datenpunkte -
geom_text_repel()für überlappungsfreie Beschriftungen -
geom_hline()/geom_vline()für Mittelwertlinien -
geom_abline()für die Regressionsgerade -
annotate()mitglue()für R², Regressionsgleichung und Mittelwerte
-
- Bei Bedarf erweitern: Selektives Labeln, Regressionsgleichung, beschriftete Mittelwerte
Zitat
@online{schmidt2026,
author = {{Dr. Paul Schmidt}},
publisher = {BioMath GmbH},
title = {7. Regressionsergebnisse professionell aufbereiten},
date = {2026-02-07},
url = {https://biomathcontent.netlify.app/de/content/r_more/07_regression_scatterplot.html},
langid = {de}
}