7. Missing Data & Outliers

To install and load all the packages used in this chapter, run the following code:

for (pkg in c("broom", "here", "janitor", "naniar", "readxl", "tidyverse")) {
  if (!require(pkg, character.only = TRUE)) install.packages(pkg)
}

library(broom)
library(here)
library(janitor)
library(naniar)
library(readxl)
library(tidyverse)

Introduction

In real-world data analysis, datasets rarely come in perfect condition. Missing values, potential outliers, and other data quality issues are common challenges. This chapter focuses on how to identify and handle these issues, and how they might affect your statistical analyses.

Data

For this chapter, we’ll work with a dataset collected during a hypothetical research project where participants’ age and vision quality (on a scale of 1-10) were recorded. The data was collected by asking 29 people around a university campus.

Import

dat <- read_excel(here("data", "vision fixed.xls"))
head(dat, n = 5)

# A tibble: 5 × 9
  Person    Ages Gender Civil_state Height Profession  Vision Distance perc_dist
  <chr>    <dbl> <chr>  <chr>        <dbl> <chr>        <dbl>    <dbl>     <dbl>
1 Andrés      25 M      S              180 Student         10      1.5        15
2 Anja        29 F      S              168 Profession…     10      4.5        45
3 Armando     31 M      S              169 Profession…      9      4.5        50
4 Carlos      25 M      M              185 Profession…      8      6          75
5 Cristina    23 F      <NA>           170 Student         10      3          30

It’s often good practice to clean up column names to ensure they’re consistent and easy to work with. You could use the rename() function from the {dplyr} package, but it can be tedious for large datasets with many columns. Instead, you can use the clean_names() function from the {janitor} package to automatically convert column names to a consistent format (e.g., all lowercase, underscores instead of spaces):

dat <- dat %>% clean_names()
head(dat, n = 5)

# A tibble: 5 × 9
  person    ages gender civil_state height profession  vision distance perc_dist
  <chr>    <dbl> <chr>  <chr>        <dbl> <chr>        <dbl>    <dbl>     <dbl>
1 Andrés      25 M      S              180 Student         10      1.5        15
2 Anja        29 F      S              168 Profession…     10      4.5        45
3 Armando     31 M      S              169 Profession…      9      4.5        50
4 Carlos      25 M      M              185 Profession…      8      6          75
5 Cristina    23 F      <NA>           170 Student         10      3          30

This is the only time we will use the janitor package in this workshop, but it is a very useful package for cleaning up messy datasets, so feel free to check out its other functions.

Goal

Similar to the previous chapter on correlation and regression, our goal is to analyze the relationship between two numeric variables: ages and vision. However, this dataset presents two additional challenges:

1. It contains missing values
2. It appears to have a potential outlier

Exploring

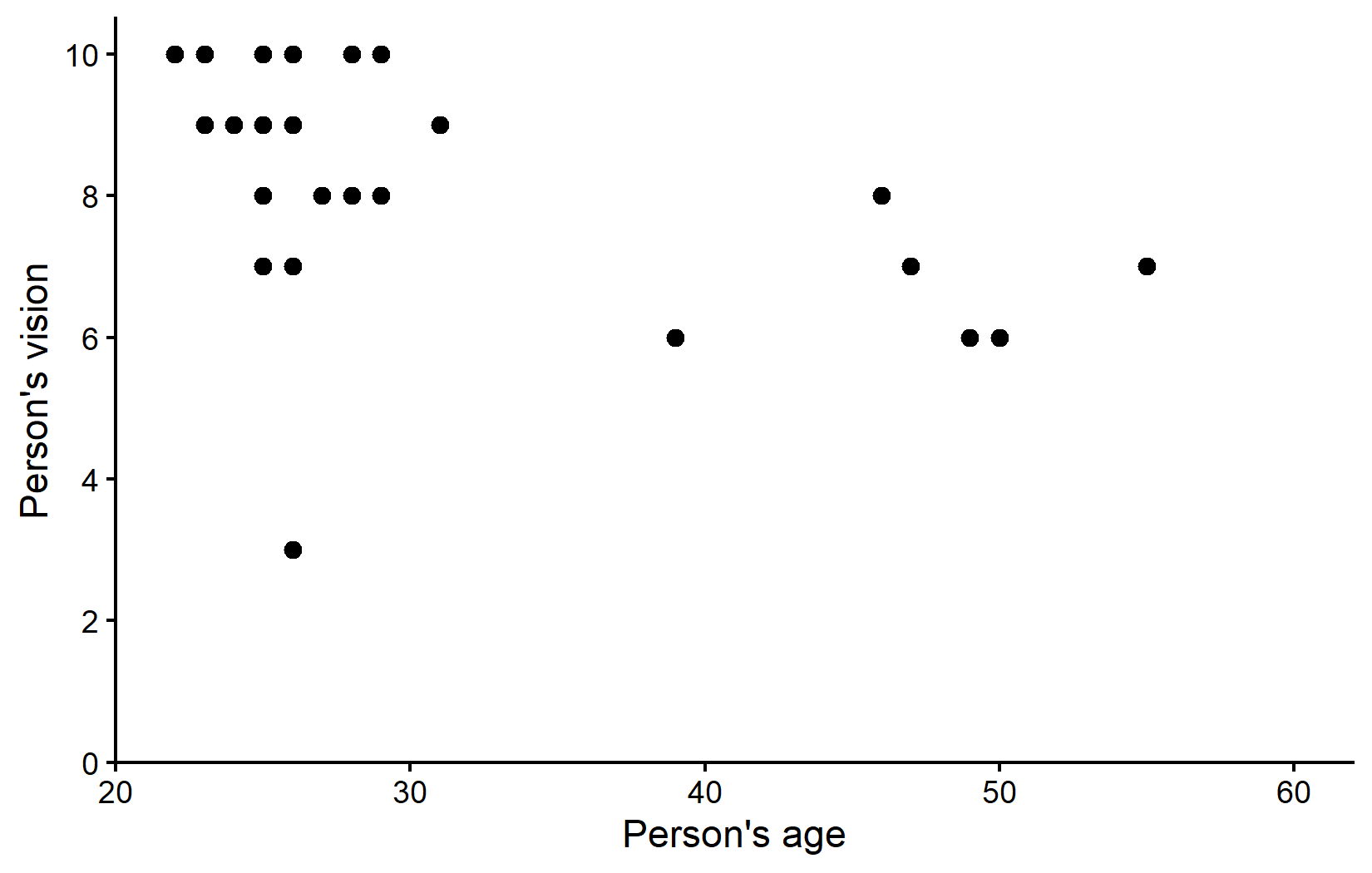
Let’s start by getting a summary of our data and visualizing the relationship between age and vision:

summary(dat)

    person               ages          gender          civil_state       
 Length:29          Min.   :22.00   Length:29          Length:29         
 Class :character   1st Qu.:25.00   Class :character   Class :character  
 Mode  :character   Median :26.00   Mode  :character   Mode  :character  
                    Mean   :30.61                                        
                    3rd Qu.:29.50                                        
                    Max.   :55.00                                        
                    NA's   :1                                            
     height       profession            vision          distance    
 Min.   :145.0   Length:29          Min.   : 3.000   Min.   :1.500  
 1st Qu.:164.8   Class :character   1st Qu.: 7.000   1st Qu.:1.500  
 Median :168.0   Mode  :character   Median : 9.000   Median :3.000  
 Mean   :168.2                      Mean   : 8.357   Mean   :3.466  
 3rd Qu.:172.8                      3rd Qu.:10.000   3rd Qu.:4.500  
 Max.   :190.0                      Max.   :10.000   Max.   :6.000  
 NA's   :1                          NA's   :1                       
   perc_dist     
 Min.   : 15.00  
 1st Qu.: 20.24  
 Median : 40.18  
 Mean   : 45.45  
 3rd Qu.: 57.19  
 Max.   :150.00  
 NA's   :1       

ggplot(data = dat) +
  aes(x = ages, y = vision) +
  geom_point(size = 2) +
  scale_x_continuous(
    name = "Person's age",
    limits = c(20, 60),
    expand = expansion(mult = c(0, 0.05))
  ) +
  scale_y_continuous(
    name = "Person's vision",
    limits = c(0, NA),
    breaks = seq(0, 10, 2),
    expand = expansion(mult = c(0, 0.05))
  ) +
  theme_classic()

Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_point()`).

The visualization suggests that most participants are in their 20s with relatively good vision scores. There appears to be a trend where older people tend to have slightly worse vision. However, there’s also a noticeable potential outlier: someone in their mid-20s with a vision score of only 3, which is substantially lower than their peers.

Handling Missing Data

While the dataset contains 29 rows, we only have complete information on 28 people. This is because there’s an NA (Not Available) value for vision for one person.

Identifying Missing Values

In R, missing values are represented by NA and require special handling. For example, to filter rows with missing values, you cannot use == NA; instead, you must use the is.na() function:

dat %>%
  filter(is.na(vision))

# A tibble: 1 × 9
  person   ages gender civil_state height profession   vision distance perc_dist
  <chr>   <dbl> <chr>  <chr>        <dbl> <chr>         <dbl>    <dbl>     <dbl>
1 Enrique    NA <NA>   <NA>            NA Professional     NA        6        NA

Here is an even smaller example for this:

c(1, 2, 3, NA) == NA # does not work properly

[1] NA NA NA NA

c(1, 2, 3, NA) %>% is.na() # works

[1] FALSE FALSE FALSE  TRUE

Some functions are sensitive to NAs

Some functions in R automatically exclude missing values, while others do not. For example, the mean() function will return NA if any of the values are missing:

c(1, 2, 3, NA) %>% mean()

[1] NA

In order for it to ignore the missing value and compute the mean of all remaining values, you need to set the na.rm argument to TRUE:

c(1, 2, 3, NA) %>% mean(na.rm = TRUE)

[1] 2

If we were to compute the average age per profession in our dataset, we would need to set the na.rm argument to TRUE in order to ignore the missing values:

dat %>%
  group_by(profession) %>%
  summarise(
    mean_age = mean(ages)
  )

# A tibble: 2 × 2
  profession   mean_age
  <chr>           <dbl>
1 Professional     NA  
2 Student          24.4

dat %>%
  group_by(profession) %>%
  summarise(
    mean_age = mean(ages, na.rm = TRUE)
  )

# A tibble: 2 × 2
  profession   mean_age
  <chr>           <dbl>
1 Professional     34.6
2 Student          24.4

Also note that when we created the ggplot above, we got a warning message about missing values: “Warning: Removed 1 row containing missing values or values outside the scale range (geom_point()).” This is because the geom_point() function automatically excludes any rows with missing values in the x or y aesthetics. The plot was still created as intended, but ggplot wants to make sure we don’t miss that there was a missing value in the data. This is a good thing, as it helps us catch potential issues early on.

Counting Missing Values

To count missing values in a dataset, the basic approach is to use sum(is.na(column)). For non-missing values, you can use sum(!is.na(column)):

dat %>%
  group_by(profession) %>%
  summarise(
    n_rows = n(),
    n_missing = sum(is.na(vision)),
    n_complete = sum(!is.na(vision))
  )

# A tibble: 2 × 4
  profession   n_rows n_missing n_complete
  <chr>         <int>     <int>      <int>
1 Professional     18         1         17
2 Student          11         0         11

The {naniar} package provides specialized functions for working with missing data that are much nicer to use:

dat %>%
  group_by(profession) %>%
  summarise(
    n_rows = n(),
    n_missing = n_miss(vision),
    n_complete = n_complete(vision)
  )

# A tibble: 2 × 4
  profession   n_rows n_missing n_complete
  <chr>         <int>     <int>      <int>
1 Professional     18         1         17
2 Student          11         0         11

These results show that we have one missing vision value in the “Student” profession category. We have already seen this one row of data above, when we filtered out Enrique via filter(is.na(vision)). At this point, let’s just remove this row from our dataset, as it won’t contribute to our analysis anyway and this way we prevent the ggplot-warning showing up every time we plot something:

dat <- dat %>%
  filter(!is.na(vision)) # !is.na() is the opposite of is.na()

Initial Correlation and Regression Analysis

Let’s proceed with our correlation and regression analysis on the dataset as is (with missing values automatically excluded).

cor <- cor.test(dat$vision, dat$ages)
tidy(cor)

# A tibble: 1 × 8
  estimate statistic p.value parameter conf.low conf.high method     alternative
     <dbl>     <dbl>   <dbl>     <int>    <dbl>     <dbl> <chr>      <chr>      
1   -0.497     -2.92 0.00709        26   -0.734    -0.153 Pearson's… two.sided  

reg <- lm(vision ~ ages, data = dat)
tidy(reg)

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)  11.1       0.996      11.2  1.97e-11
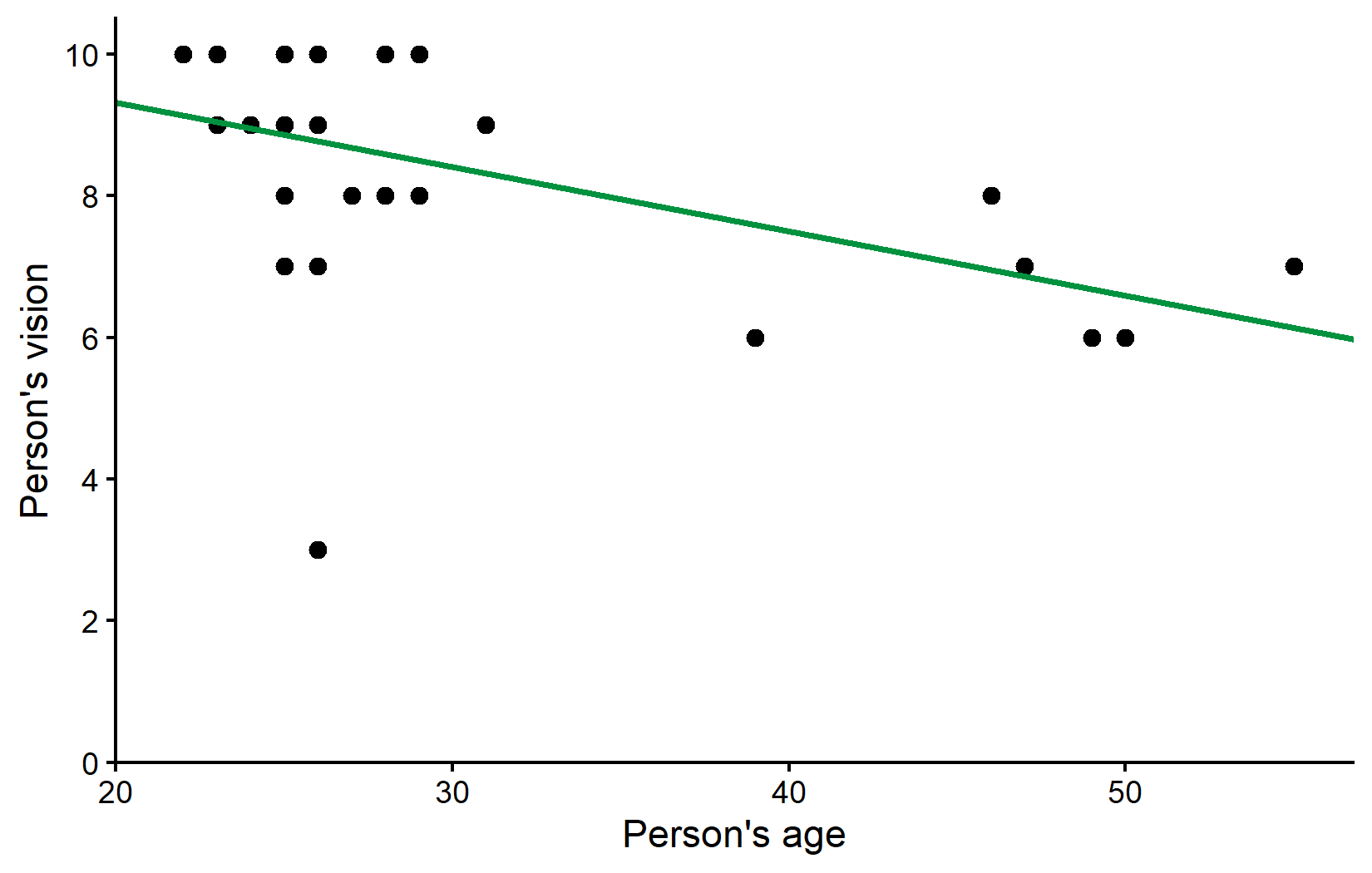
2 ages         -0.0910    0.0311     -2.92 7.09e- 3

We have a moderate negative correlation of approximately -0.5, which is statistically significant (p < 0.05). The regression equation is:

vision = 11.14 - 0.09 × ages

Let’s visualize this relationship with our regression line:

ggplot(data = dat) +
  aes(x = ages, y = vision) +
  geom_point(size = 2) +
  geom_abline(
    intercept = reg$coefficients[1],
    slope = reg$coefficients[2],
    color = "#00923f",
    linewidth = 1
  ) +
  scale_x_continuous(
    name = "Person's age",
    limits = c(20, 55),
    expand = expansion(mult = c(0, 0.05))
  ) +
  scale_y_continuous(
    name = "Person's vision",
    limits = c(0, NA),
    breaks = seq(0, 10, 2),
    expand = expansion(mult = c(0, 0.05))
  ) +
  theme_classic()

Dealing with Outliers

NoteAdditional Resources

Here, we discuss manually and thus subjectively identifying a data point as a potential outlier. We do not discuss automatic and thus objective approaches for outlier detection, but see e.g. here or here if you are interested in that.

Looking at our plot, there appears to be one data point that stands out: someone in their mid-20s with a vision score of only 3, which is considerably lower than all other participants of similar age.

Step 1: Investigate the Potential Outlier

When you identify a potential outlier, the first step is to investigate it further. Let’s find out more about this data point:

dat %>%
  filter(vision == 3)

# A tibble: 1 × 9
  person   ages gender civil_state height profession   vision distance perc_dist
  <chr>   <dbl> <chr>  <chr>        <dbl> <chr>         <dbl>    <dbl>     <dbl>
1 Rolando    26 M      M              180 Professional      3      4.5       150

We find that the potential outlier is a 26-year-old named Rolando with a vision score of 3.

Step 2: Make an Informed Decision

In real research, at this point you would:

1. Check your original data collection records to confirm this wasn’t a recording error
2. Consider your knowledge of the participant (if applicable) to determine if there were any special circumstances
3. Decide whether this value is a genuine observation or an error that should be corrected or removed

For this example, let’s assume we’ve decided to analyze our data both with and without this potential outlier to see how it affects our results.

Analysis Without the Outlier

Let’s create a new dataset excluding Rolando:

dat_no_outlier <- dat %>%
  filter(person != "Rolando")

Now, let’s repeat our correlation and regression analysis:

cor_no_outlier <- cor.test(dat_no_outlier$vision, dat_no_outlier$ages)
reg_no_outlier <- lm(vision ~ ages, data = dat_no_outlier)

Comparing Results

Let’s compare the correlation results:

# With outlier
tidy(cor) %>% select(1, 3, 5, 6)

# A tibble: 1 × 4
  estimate p.value conf.low conf.high
     <dbl>   <dbl>    <dbl>     <dbl>
1   -0.497 0.00709   -0.734    -0.153

# Without outlier
tidy(cor_no_outlier) %>% select(1, 3, 5, 6)

# A tibble: 1 × 4
  estimate   p.value conf.low conf.high
     <dbl>     <dbl>    <dbl>     <dbl>
1   -0.696 0.0000548   -0.851    -0.430

The correlation coefficient increased from -0.5 to -0.7 after removing the outlier, indicating a stronger negative relationship between age and vision. This is a quite drastic change considering that we removed only a single data point.

And the regression results:

# With outlier
tidy(reg) %>% select(1, 2, 3)

# A tibble: 2 × 3
  term        estimate std.error
  <chr>          <dbl>     <dbl>
1 (Intercept)  11.1       0.996 
2 ages         -0.0910    0.0311

# Without outlier
tidy(reg_no_outlier) %>% select(1, 2, 3)

# A tibble: 2 × 3
  term        estimate std.error
  <chr>          <dbl>     <dbl>
1 (Intercept)   11.7      0.679 
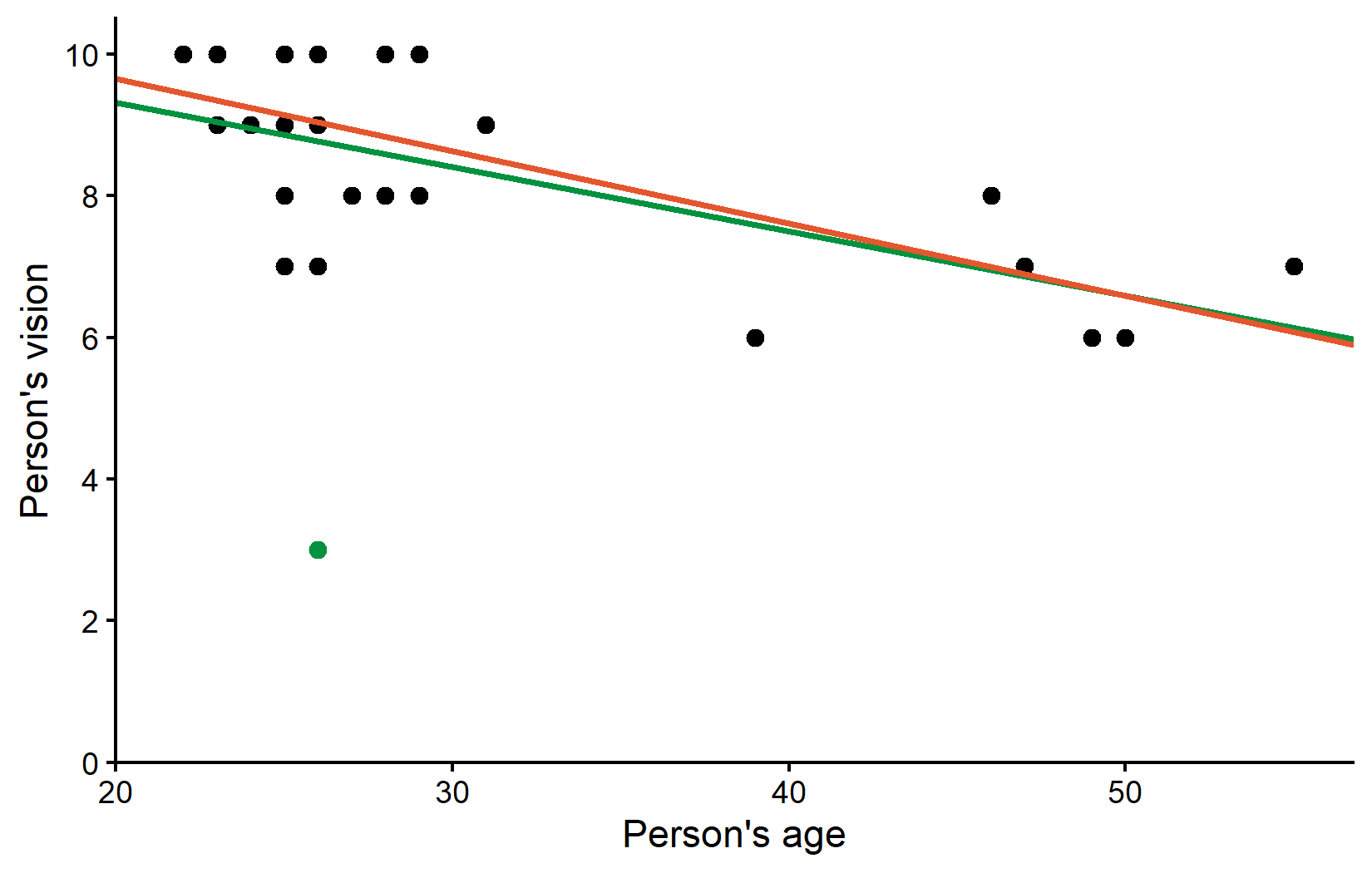
2 ages          -0.102    0.0211

These values did actually not change so much it seems. Before removing Rolando the estimated model was vision = 11.1 - 0.0910*ages and after removing him it is vision = 11.7 - 0.102*ages. We can also visualize the regression line without the outlier (orange) side-by-side with the regression line including the outlier (green) from before:

ggplot() +
  aes(x = ages, y = vision) +
  # Plot all points of dat_no_outlier in standard black
  geom_point(
    data = dat_no_outlier,
    size = 2
  ) +
  # Plot only Rolando as green point
  geom_point(
    data = dat %>% filter(person == "Rolando"),
    color = "#00923f",
    size = 2
  ) +
  # Plot regression line with outlier in green
  geom_abline(
    intercept = reg$coefficients[1],
    slope = reg$coefficients[2],
    color = "#00923f",
    linewidth = 1
  ) +
  # Plot regression line without outlier in orange
  geom_abline(
    intercept = reg_no_outlier$coefficients[1],
    slope = reg_no_outlier$coefficients[2],
    color = "#e4572e",
    linewidth = 1
  ) +
  scale_x_continuous(
    name = "Person's age",
    limits = c(20, 55),
    expand = expansion(mult = c(0, 0.05))
  ) +
  scale_y_continuous(
    name = "Person's vision",
    limits = c(0, NA),
    breaks = seq(0, 10, 2),
    expand = expansion(mult = c(0, 0.05))
  ) +
  theme_classic()

So the correlation estimate changed quite a bit, but the regression estimates did not change that much. However, at this point it makes sense to ask how well each fitted regression line fits the respective dataset:

Coefficient of Determination

A useful metric for comparing regression models is the coefficient of determination (R²), which measures the proportion of variance explained by the model. We can get this information from our fitted regression models (reg and reg_no_outlier) either via summary() or once again with a function from the {broom} package, i.e. glance():

# With outlier
glance(reg) %>% select(contains("r.squared"))

# A tibble: 1 × 2
  r.squared adj.r.squared
      <dbl>         <dbl>
1     0.247         0.218

# Without outlier
glance(reg_no_outlier) %>% select(contains("r.squared"))

# A tibble: 1 × 2
  r.squared adj.r.squared
      <dbl>         <dbl>
1     0.485         0.464

So while the regression lines (or rather their parameter estimates) may not have changed that much, the explanatory power of our model nearly doubled after removing the outlier. The R² value increased from 25% to 49%, indicating that the model without the outlier explains a much larger proportion of the variance in vision scores. In other words: The orange line explains all data points except Rolando much better than the green line explains all data points including Rolando.

Wrapping Up

This chapter has demonstrated the importance of carefully examining your data for quality issues before conducting statistical analyses. We’ve seen how a single outlier can substantially impact correlation and regression results.

NoteKey Takeaways

Summary & Key Takeaways

1. Data Quality Assessment:
   • Always check for missing values and potential outliers before analysis
   • Use functions like is.na(), summary(), and visualization to identify issues
2. Handling Missing Data:
   • R typically excludes missing values (NA) automatically in functions like cor.test() and lm()
   • Packages like {naniar} provide specialized tools for working with missing data
   • Always document how many values were missing and how they were handled
3. Dealing with Outliers:
   • Investigate potential outliers to determine if they represent errors or genuine observations
   • Consider analyzing data both with and without outliers to understand their impact
   • Be transparent about any data points removed and the rationale
4. Impact on Statistical Analysis:
   • Removing Rolando (our outlier) changed the correlation from -0.5 to -0.7
   • The R² value increased from 25% to 49% after removing the outlier
   • While parameter estimates didn’t change dramatically, the explanatory power of our model nearly doubled
5. Best Practices:
   • Never remove outliers solely to improve your results
   • Document all data cleaning decisions
   • Consider reporting results both with and without outliers when appropriate

Remember that while statistical tools can help identify potential issues, the decision to include or exclude data points should be based on sound scientific reasoning rather than statistical convenience, if feasible. Always be transparent about your data handling decisions in any research report.