5. Einfaktorielle ANOVA im Augmented Design

Varianzanalyse (ANOVA); Augmented Design mit Standardsorten

Author
Zugehörigkeit

Dr. Paul Schmidt

BioMath GmbH

Last updated

8. Februar 2026

Um alle in diesem Kapitel verwendeten Pakete zu installieren und zu laden, führen Sie folgenden Code aus:

for (pkg in c("desplot", "emmeans", "ggtext", "here", "lme4", 
              "lmerTest", "multcomp", "multcompView", "tidyverse")) {
  if (!require(pkg, character.only = TRUE)) install.packages(pkg)
}

library(desplot)
library(emmeans)
library(ggtext)
library(here)
library(lme4)
library(lmerTest)
library(multcomp)
library(multcompView)
library(tidyverse)

Augmented Designs

Im vorherigen Kapitel haben wir ein Alpha-Design analysiert, bei dem alle Genotypen über Blöcke hinweg repliziert wurden. In der Pflanzenzüchtung und Sortenprüfung stehen wir jedoch oft vor Situationen, in denen wir viele neue Genotypen testen müssen, aber nur begrenzte Ressourcen haben. Die Prüfung aller Genotypen mit vollständiger Replikation ist möglicherweise nicht durchführbar.

Was ist ein Augmented Design?

Ein Augmented Design (auch erweitertes Blockdesign genannt) adressiert dies durch die Aufnahme von zwei Arten von Einträgen:

  1. Standardsorten (Checks): Repliziert über alle Blöcke, bieten eine Basis für die Schätzung von Blockeffekten
  2. Neue Einträge (Prüfgenotypen): Nicht repliziert, erscheinen nur in jeweils einem Block

Die replizierten Standards ermöglichen es uns, Blockeffekte zu schätzen und zu adjustieren, die dann auf die nicht replizierten Einträge angewendet werden können. Dieses Design maximiert die Anzahl neuer Einträge, die mit begrenzten Ressourcen getestet werden können, und ermöglicht dennoch valide statistische Vergleiche.

Die Vorteile von Augmented Designs umfassen:

  1. Ressourceneffizienz: Viele neue Einträge ohne vollständige Replikation testen
  2. Valide Vergleiche: Aus Standards geschätzte Blockeffekte werden auf alle Einträge angewendet
  3. Flexibilität: Kann unterschiedliche Anzahlen neuer Einträge pro Block aufnehmen
  4. Praktisch für Screening: Ideal für frühe Sortenprüfungen mit vielen Kandidaten

Der Kompromiss

Der wesentliche Kompromiss ist die Präzision: Nicht replizierte Einträge haben höhere Standardfehler als replizierte Standards. Das bedeutet, dass Vergleiche mit neuen Einträgen weniger präzise sind als Vergleiche zwischen Standards. Für anfängliche Screening-Zwecke ist dies jedoch oft akzeptabel.

Daten

Dieses Beispiel betrachtet Daten, die in Petersen (1994) veröffentlicht wurden, aus einem Ertragsversuch, der als Augmented Design angelegt wurde. Der Versuch umfasste 3 Standardsorten (st, ci, wa), die in allen 6 Blöcken repliziert wurden, und 30 neue Einträge (nummeriert 1-30), die jeweils nur in einem Block erschienen.

Import

dat <- read_csv(here("data", "Petersen1994.csv"))
dat
Rows: 48 Columns: 5
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (2): gen, block
dbl (3): yield, row, col

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
# A tibble: 48 × 5
   gen   yield block   row   col
   <chr> <dbl> <chr> <dbl> <dbl>
 1 st     2972 I         1     1
 2 14     2405 I         2     1
 3 26     2855 I         3     1
 4 ci     2592 I         4     1
 5 17     2572 I         5     1
 6 wa     2608 I         6     1
 7 22     2705 I         7     1
 8 13     2391 I         8     1
 9 st     3122 II        1     2
10 ci     3023 II        2     2
# ℹ 38 more rows

Der Datensatz enthält:

  • gen: Genotypbezeichnung (3 Standards: st, ci, wa; 30 neue Einträge: 1-30)
  • yield: Ernteertrag
  • block: Sechs Blöcke (I-VI)
  • row und col: Feldparzellenkoordinaten für die Visualisierung

Formatierung

Vor der Analyse müssen wir gen und block als Faktoren kodieren:

dat <- dat %>%
  mutate(across(c(gen, block), ~ as.factor(.x)))

dat
# A tibble: 48 × 5
   gen   yield block   row   col
   <fct> <dbl> <fct> <dbl> <dbl>
 1 st     2972 I         1     1
 2 14     2405 I         2     1
 3 26     2855 I         3     1
 4 ci     2592 I         4     1
 5 17     2572 I         5     1
 6 wa     2608 I         6     1
 7 22     2705 I         7     1
 8 13     2391 I         8     1
 9 st     3122 II        1     2
10 ci     3023 II        2     2
# ℹ 38 more rows

Erkunden

Betrachten wir zunächst die deskriptiven Statistiken. Beachten Sie den Unterschied in der Replikation zwischen Standards und neuen Einträgen:

dat %>% 
  group_by(gen) %>% 
  summarize(
    count = n(),
    mean_yield = mean(yield),
    sd_yield = sd(yield)
  ) %>%
  arrange(desc(count), desc(mean_yield))
# A tibble: 33 × 4
   gen   count mean_yield sd_yield
   <fct> <int>      <dbl>    <dbl>
 1 st        6      2759.     832.
 2 ci        6      2726.     711.
 3 wa        6      2678.     615.
 4 19        1      3643       NA 
 5 11        1      3380       NA 
 6 07        1      3265       NA 
 7 03        1      3055       NA 
 8 04        1      3018       NA 
 9 01        1      3013       NA 
10 30        1      2955       NA 
# ℹ 23 more rows

Die drei Standards (ci, st, wa) erscheinen jeweils 6 mal (einmal pro Block), während alle neuen Einträge nur einmal erscheinen. Dies ist das definierende Merkmal eines Augmented Designs.

Schauen wir uns nun die Blockstruktur an:

dat %>% 
  group_by(block) %>% 
  summarize(
    count = n(),
    mean_yield = mean(yield),
    sd_yield = sd(yield)
  ) %>%
  arrange(desc(mean_yield))
# A tibble: 6 × 4
  block count mean_yield sd_yield
  <fct> <int>      <dbl>    <dbl>
1 VI        8      3205.     417.
2 II        8      2864.     258.
3 IV        8      2797.     445.
4 I         8      2638.     202.
5 III       8      2567.     440.
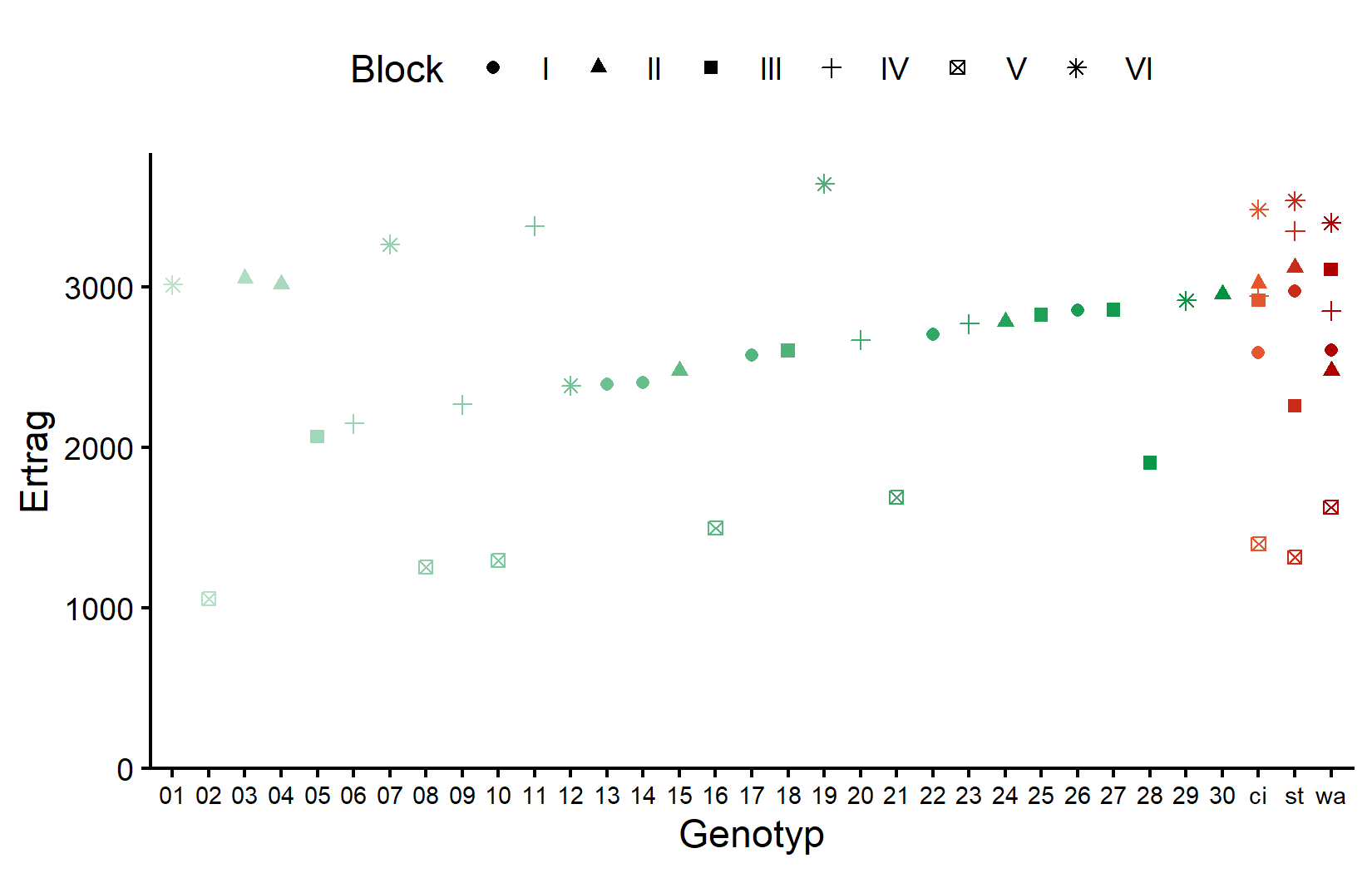
6 V         8      1390.     207.

Wir können Variation zwischen den Blöcken sehen. Block II hat den höchsten mittleren Ertrag, während Block V den niedrigsten hat. Visualisieren wir die Daten mit verschiedenen Farben für Standards und neue Einträge:

# Benutzerdefinierte Farben definieren: Grün für neue Einträge, Rot für Standards
greens30 <- colorRampPalette(c("#bce2cc", "#00923f"))(30)
oranges3 <- colorRampPalette(c("#e4572e", "#ad0000"))(3)
gen_cols <- set_names(c(greens30, oranges3), nm = levels(dat$gen))
ggplot(data = dat) +
  aes(
    y = yield,
    x = gen,
    color = gen,
    shape = block
  ) +
  geom_point() +
  scale_x_discrete(
    name = "Genotyp"
  ) +
  scale_y_continuous(
    name = "Ertrag",
    limits = c(0, NA),
    expand = expansion(mult = c(0, 0.05))
  ) +
  scale_color_manual(
    guide = "none",
    values = gen_cols
  ) +
  scale_shape_discrete(
    name = "Block"
  ) +
  guides(shape = guide_legend(nrow = 1)) +
  theme_classic() +
  theme(
    legend.position = "top",
    axis.text.x = element_text(size = 7)
  )

Die Standards (in rot/orange auf der rechten Seite) zeigen Variation über Blöcke hinweg, was uns ermöglicht, Blockeffekte zu schätzen. Schauen wir uns nun das Feldlayout an:

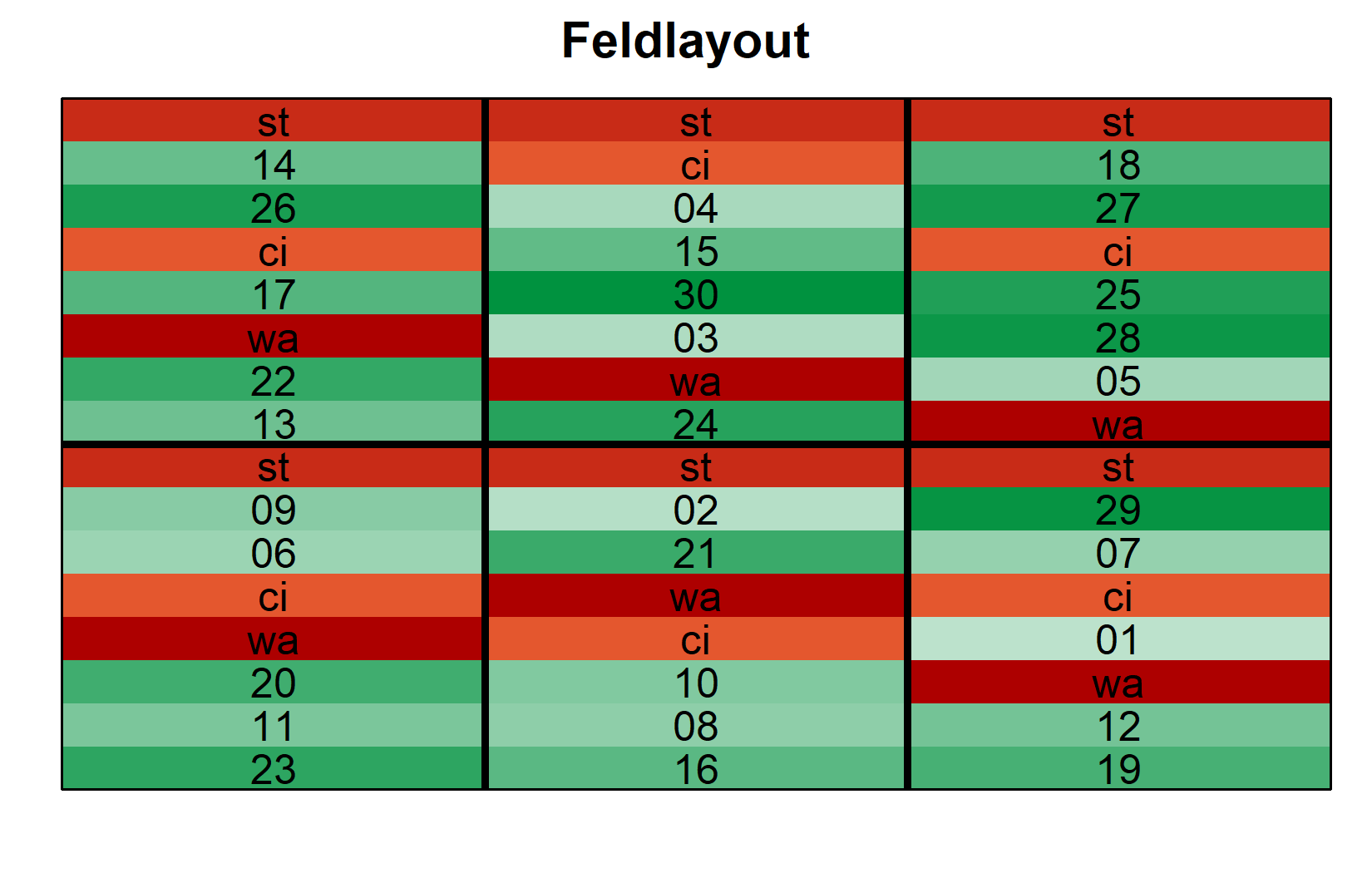
desplot(
  data = dat,
  flip = TRUE,
  form = gen ~ col + row, # Füllfarbe pro Genotyp  
  col.regions = gen_cols, # benutzerdefinierte Füllfarben
  out1 = block, # Linie zwischen Blöcken                     
  text = gen, # Genotypnamen pro Parzelle
  cex = 1,
  shorten = FALSE,
  main = "Feldlayout",
  show.key = FALSE
)

Das Layout zeigt, wie Standards (st, ci, wa) über alle Blöcke verteilt sind, während jeder neue Eintrag nur in einem Block erscheint.

Modell und ANOVA

Modell mit festen Bloecken

Für ein Augmented Design können wir das Modell mit Blöcken als entweder feste oder zufällige Effekte anpassen. Beginnen wir mit festen Blöcken:

mod_fb <- lm(yield ~ gen + block, data = dat)

Und vergleichen mit zufälligen Blöcken:

mod_rb <- lmer(yield ~ gen + (1 | block), data = dat)

Um zu bestimmen, welches Modell für den Vergleich von Genotypen besser geeignet ist, vergleichen wir den durchschnittlichen Standardfehler einer Differenz (s.e.d.):

# s.e.d. für Modell mit festen Blöcken
sed_fixed <- mod_fb %>%
  emmeans(pairwise ~ "gen", adjust = "none") %>%
  pluck("contrasts") %>%
  as_tibble() %>%
  pull("SE") %>%
  mean()

# s.e.d. für Modell mit zufälligen Blöcken  
sed_random <- mod_rb %>%
  emmeans(pairwise ~ "gen", adjust = "none", lmer.df = "kenward-roger") %>%
  pluck("contrasts") %>%
  as_tibble() %>%
  pull("SE") %>%
  mean()

tibble(
  model = c("Feste Blöcke", "Zufällige Blöcke"),
  mean_sed = c(sed_fixed, sed_random)
)
# A tibble: 2 × 2
  model            mean_sed
  <chr>               <dbl>
1 Feste Blöcke         461.
2 Zufällige Blöcke     462.

In diesem Fall hat das Modell mit festen Blöcken einen etwas kleineren s.e.d., daher verwenden wir es für unsere Analyse.

An dieser Stelle (d.h. nach dem Modell-Fit und vor der ANOVA-Interpretation) sollte man prüfen, ob die Modellannahmen erfüllt sind. Mehr dazu im Anhang A1: Modelldiagnostik.

Durchführung der ANOVA

ANOVA <- anova(mod_fb)
ANOVA
Analysis of Variance Table

Response: yield
          Df   Sum Sq Mean Sq F value    Pr(>F)    
gen       32 12626173  394568   4.331 0.0091056 ** 
block      5  6968486 1393697  15.298 0.0002082 ***
Residuals 10   911027   91103                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Der Genotypeffekt ist statistisch signifikant (p < 0.05), was auf Unterschiede zwischen Genotypen hinweist. Der Blockeffekt ist ebenfalls signifikant, was bestätigt, dass die Blockbildung vorteilhaft war.

Mittelwertvergleiche

mean_comp <- mod_fb %>% 
  emmeans(specs = ~ gen) %>%
  cld(adjust = "tukey", Letters = letters)

mean_comp
 gen emmean  SE df lower.CL upper.CL .group
 12    1632 341 10      164     3100  a    
 06    1823 341 10      355     3291  a    
 28    1862 341 10      394     3330  a    
 09    1943 341 10      475     3411  a    
 05    2024 341 10      556     3492  a    
 29    2162 341 10      694     3630  a    
 01    2260 341 10      792     3728  a    
 15    2324 341 10      856     3792  a    
 02    2330 341 10      862     3798  a    
 20    2345 341 10      877     3813  a    
 13    2388 341 10      920     3856  a    
 14    2402 341 10      934     3870  a    
 23    2445 341 10      977     3913  a    
 07    2512 341 10     1044     3980  a    
 08    2528 341 10     1060     3996  a    
 18    2562 341 10     1094     4030  a    
 10    2568 341 10     1100     4036  a    
 17    2569 341 10     1101     4037  a    
 24    2630 341 10     1162     4098  a    
 wa    2678 123 10     2148     3208  a    
 22    2702 341 10     1234     4170  a    
 ci    2726 123 10     2195     3256  a    
 st    2759 123 10     2229     3289  a    
 16    2770 341 10     1302     4238  a    
 25    2784 341 10     1316     4252  a    
 30    2802 341 10     1334     4270  a    
 27    2816 341 10     1348     4284  a    
 26    2852 341 10     1384     4320  a    
 04    2865 341 10     1397     4333  a    
 19    2890 341 10     1422     4358  a    
 03    2902 341 10     1434     4370  a    
 21    2963 341 10     1495     4431  a    
 11    3055 341 10     1587     4523  a    

Results are averaged over the levels of: block 
Confidence level used: 0.95 
Conf-level adjustment: sidak method for 33 estimates 
P value adjustment: tukey method for comparing a family of 33 estimates 
significance level used: alpha = 0.05 
NOTE: If two or more means share the same grouping symbol,
      then we cannot show them to be different.
      But we also did not show them to be the same.

Beachten Sie, dass obwohl einige Genotypen höhere adjustierte Mittelwerte haben als andere, mit Tukey-Adjustierung keine signifikanten Unterschiede erkannt werden. Dies liegt teilweise daran, dass nicht replizierte Einträge große Konfidenzintervalle haben. Zum Beispiel hat Genotyp 11 den höchsten adjustierten Mittelwert (3055), aber sein Konfidenzintervall ist breit.

Visualisierung der Ergebnisse

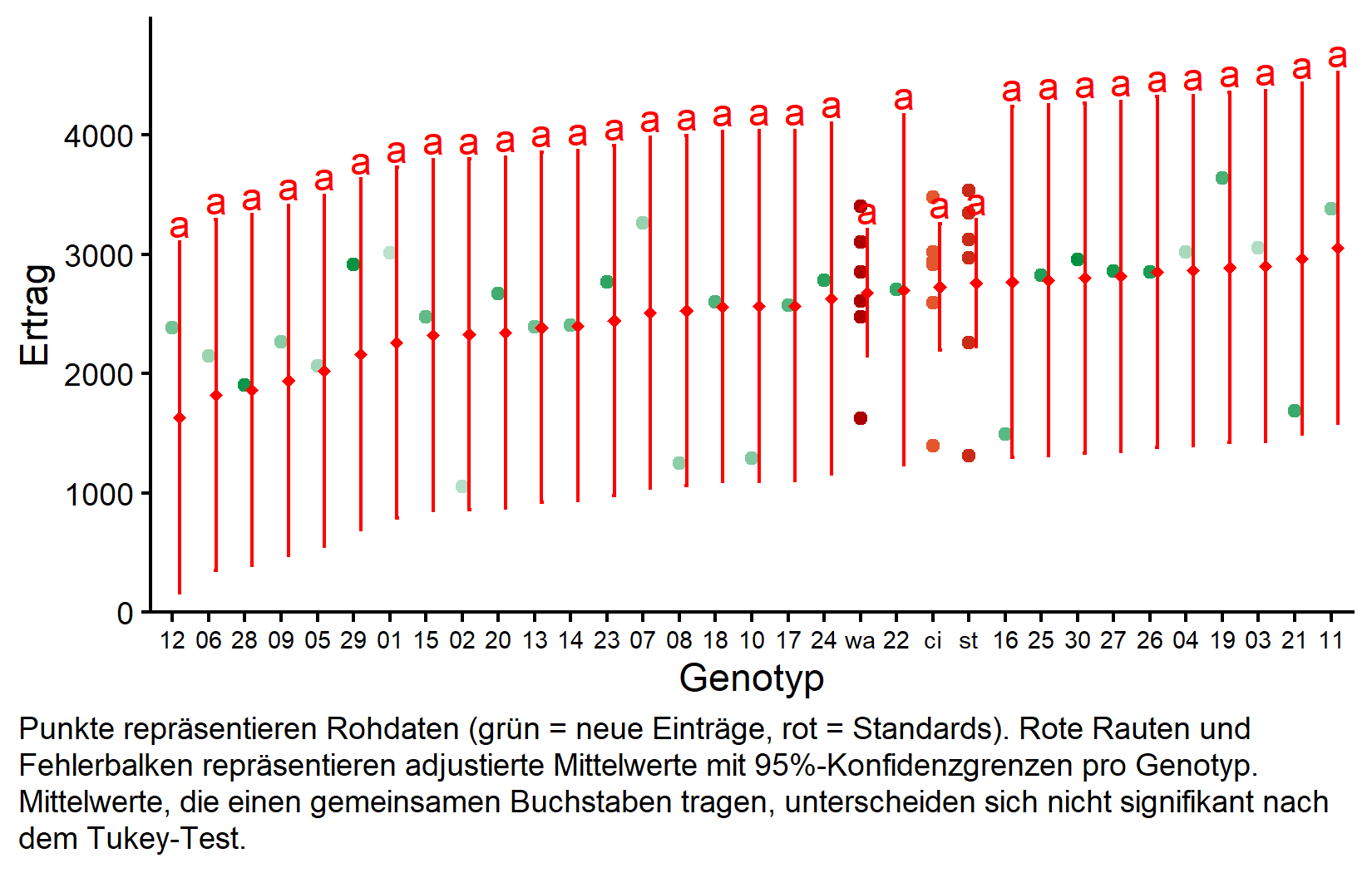
my_caption <- "Punkte repräsentieren Rohdaten (grün = neue Einträge, rot = Standards). Rote Rauten und Fehlerbalken repräsentieren adjustierte Mittelwerte mit 95%-Konfidenzgrenzen pro Genotyp. Mittelwerte, die einen gemeinsamen Buchstaben tragen, unterscheiden sich nicht signifikant nach dem Tukey-Test."

ggplot() +
  aes(x = gen) +
  # farbige Punkte für die Rohdaten
  geom_point(
    data = dat,
    aes(y = yield, color = gen)
  ) +
  # rote Rauten für die adjustierten Mittelwerte
  geom_point(
    data = mean_comp,
    aes(y = emmean),
    shape = 18,
    color = "red",
    position = position_nudge(x = 0.2)
  ) +
  # rote Fehlerbalken für die Konfidenzgrenzen der adjustierten Mittelwerte
  geom_errorbar(
    data = mean_comp,
    aes(ymin = lower.CL, ymax = upper.CL),
    color = "red",
    width = 0.1,
    position = position_nudge(x = 0.2)
  ) +
  # rote Buchstaben 
  geom_text(
    data = mean_comp,
    aes(y = upper.CL, label = str_trim(.group)),
    color = "red",
    vjust = -0.2,
    position = position_nudge(x = 0.2)
  ) + 
  scale_color_manual(
    guide = "none", 
    values = gen_cols
  ) + 
  scale_x_discrete(
    name = "Genotyp",
    limits = as.character(mean_comp$gen)
  ) +
  scale_y_continuous(
    name = "Ertrag",
    limits = c(0, NA),
    expand = expansion(mult = c(0, 0.1))
  ) +
  labs(caption = my_caption) +
  theme_classic() +
  theme(plot.caption = element_textbox_simple(margin = margin(t = 5)),
        plot.caption.position = "plot", 
        axis.text.x = element_text(size = 7))

Die Darstellung zeigt deutlich den Unterschied in der Präzision: Standards (auf der rechten Seite) haben viel schmalere Konfidenzintervalle aufgrund der Replikation, während neue Einträge breite Intervalle haben, die auf Einzelbeobachtungen basieren, die für Blockeffekte adjustiert wurden.

Bonus: Varianzkomponenten

Wir können Varianzkomponenten aus beiden Modellen extrahieren, um die Variationsquellen zu verstehen:

# Residualvarianz aus dem festen Modell
tibble(
  source = "Residual (festes Modell)",
  variance = summary(mod_fb)$sigma^2
)
# A tibble: 1 × 2
  source                   variance
  <chr>                       <dbl>
1 Residual (festes Modell)   91103.
# Varianzkomponenten aus dem zufälligen Modell
as_tibble(VarCorr(mod_rb)) %>%
  select(grp, variance = vcov)
# A tibble: 2 × 2
  grp      variance
  <chr>       <dbl>
1 block     434198.
2 Residual   91103.

Zusammenfassung

Sie haben nun gelernt, wie man Daten aus einem Augmented Design analysiert, das besonders nützlich ist für das Screening vieler neuer Einträge mit begrenzten Ressourcen.

HinweisWichtige Erkenntnisse

  1. Augmented Designs enthalten replizierte Standards und nicht replizierte neue Einträge, wodurch die Anzahl der Einträge maximiert wird, die getestet werden können.

  2. Standards schätzen Blockeffekte, die dann zur Adjustierung aller Einträge verwendet werden, einschließlich der nicht replizierten.

  3. Der Kompromiss ist die Präzision: Nicht replizierte Einträge haben breitere Konfidenzintervalle als replizierte Standards.

  4. Die Modellwahl (feste vs. zufällige Blöcke) kann darauf basieren, welche den kleineren durchschnittlichen s.e.d. für Genotypvergleiche ergibt.

  5. Praktische Anwendung: Augmented Designs sind ideal für frühe Screening-Versuche, bei denen viele Kandidaten eine erste Bewertung benötigen.

  6. Vorsicht bei der Interpretation: Das Fehlen signifikanter Unterschiede bedeutet nicht, dass Einträge gleich sind - es kann geringe Power für nicht replizierte Vergleiche widerspiegeln.

Literatur

Petersen, Roger G. 1994. Agricultural Field Experiments. CRC Press. https://doi.org/10.1201/9781482277371.

Zitat

Mit BibTeX zitieren:
@online{schmidt2026,
  author = {{Dr. Paul Schmidt}},
  publisher = {BioMath GmbH},
  title = {5. Einfaktorielle ANOVA im Augmented Design},
  date = {2026-02-08},
  url = {https://biomathcontent.netlify.app/de/content/lin_mod_exp/05_oneway_augmented.html},
  langid = {de}
}
Bitte zitieren Sie diese Arbeit als:
Dr. Paul Schmidt. 2026. “5. Einfaktorielle ANOVA im Augmented Design.” BioMath GmbH. February 8, 2026. https://biomathcontent.netlify.app/de/content/lin_mod_exp/05_oneway_augmented.html.