Um alle in diesem Kapitel verwendeten Pakete zu installieren und zu laden, führen Sie folgenden Code aus:
Vom RCBD zum Lateinischen Quadrat
Im vorherigen Kapitel haben wir Daten aus einem randomisierten vollständigen Blockdesign (RCBD) analysiert, bei dem wir eine Quelle systematischer Variation durch Gruppierung der Versuchseinheiten in Blöcke kontrolliert haben. Das RCBD ermöglichte es uns, einen Gradienten oder eine Quelle der Heterogenität in unserem Versuchsmaterial zu berücksichtigen.
Allerdings stehen landwirtschaftliche Experimente manchmal vor Situationen, in denen zwei Quellen systematischer Variation gleichzeitig kontrolliert werden müssen:
- Felder können Gradienten sowohl in der Bodenfruchtbarkeit (Nord-Süd) als auch in der Entwässerung (Ost-West) aufweisen
- Gewächshausexperimente können sowohl Lichtgradienten als auch Temperaturvariationen über die Tische hinweg haben
- Laborexperimente können sowohl Positionseffekte als auch zeitbasierte Effekte aufweisen
Warum ein Lateinisches Quadrat verwenden?
Ein Lateinisches Quadrat (Latin Square Design, LSD) adressiert dies, indem es zwei orthogonale Variationsquellen gleichzeitig kontrolliert. In einem Lateinischen Quadrat werden die Behandlungen so angeordnet, dass jede Behandlung genau einmal in jeder Zeile und genau einmal in jeder Spalte erscheint. Dies stellt sicher, dass Behandlungsvergleiche weder mit Zeileneffekten noch mit Spalteneffekten vermengt sind.
Die Vorteile eines Lateinischen Quadrats umfassen:
- Kontrolle von zwei Variationsquellen: Sowohl Zeilen- als auch Spalteneffekte werden aus dem Versuchsfehler entfernt
- Erhöhte Präzision: Wenn sowohl Zeilen- als auch Spalteneffekte vorhanden sind und keine Zeile × Spalte Interaktionen existieren, kann eine größere Reduktion der unerklärten Variation als mit RCBD erreicht werden
- Ausgewogene Vergleiche: Jede Behandlung wird den gleichen Zeilen- und Spaltenbedingungen ausgesetzt
- Kompaktes Design: Erfordert weniger Versuchseinheiten als einige alternative Designs, wenn die Bedingungen geeignet sind
Betrachten Sie die Progression: CRD hat nur zufällige Variation, RCBD kontrolliert eine systematische Quelle, und das Lateinische Quadrat kontrolliert zwei systematische Variationsquellen.
Designanforderungen und Annahmen
Ein Lateinisches Quadrat erfordert:
- Die gleiche Anzahl von Behandlungen, Zeilen und Spalten (z.B. 4×4 Quadrat für 4 Behandlungen)
- Jede Behandlung erscheint genau einmal in jeder Zeile
- Jede Behandlung erscheint genau einmal in jeder Spalte
- Zufällige Anordnung unter diesen Einschränkungen
Kritische Annahme: Das Design nimmt an, dass keine Interaktion zwischen Zeilen- und Spalteneffekten besteht. Wenn Zeile × Spalte Interaktionen existieren, kann das Lateinische Quadrat weniger effizient sein als alternative Designs.
Dies macht Lateinische Quadrate am praktischsten bei kleineren Behandlungszahlen (typischerweise 3-6 Behandlungen). Bei mehr als 6 Behandlungen wird das Design unhandlich und alternative Designs werden oft bevorzugt.
Wann KEINE Lateinischen Quadrate verwenden
Lateinische Quadrate sind nicht geeignet, wenn:
- Sie mehr als 6-7 Behandlungen haben (wird unpraktisch)
- Zeile × Spalte Interaktionen erwartet oder vermutet werden
- Die Zeilen- und Spalten-Blockungsfaktoren tatsächlich keine Quellen systematischer Variation sind
- Sie mehr Replikation benötigen als das Design erlaubt
- Faktorielle Behandlungsstrukturen die Untersuchung von Behandlungsinteraktionen erfordern
In solchen Fällen können andere Designs wie RCBD mit mehreren Blöcken, Split-Plot-Designs oder faktorielle Anordnungen geeigneter sein.
Daten
Für dieses Beispiel verwenden wir Daten von Bridges (1989), die den Gurkenertrag mit vier verschiedenen Genotypen untersuchen. Das Experiment wurde als 4×4 Lateinisches Quadrat angelegt, um potenzielle Zeilen- und Spalteneffekte im Feld zu kontrollieren. Dieser Datensatz ist über das {agridat}-Paket verfügbar, das viele landwirtschaftliche Datensätze enthält.
Import
# A tibble: 16 × 4
gen row col yield
<fct> <int> <int> <dbl>
1 Dasher 1 3 44.2
2 Dasher 2 4 54.1
3 Dasher 3 2 47.2
4 Dasher 4 1 36.7
5 Guardian 1 4 33
6 Guardian 2 2 13.6
7 Guardian 3 1 44.1
8 Guardian 4 3 35.8
9 Poinsett 1 1 11.5
10 Poinsett 2 3 22.4
11 Poinsett 3 4 30.3
12 Poinsett 4 2 21.5
13 Sprint 1 2 15.1
14 Sprint 2 1 20.3
15 Sprint 3 3 41.3
16 Sprint 4 4 27.1Der ursprüngliche Datensatz enthält Versuche an zwei Standorten, aber wir konzentrieren uns nur auf den Versuch am Standort Clemson. Der Datensatz enthält:
-
gen: Vier Genotypen (Cherokee, Dasher, Gemini und Poinsett) -
yield: Gurkenertrag für jede Parzelle -
row: Zeilenposition im Feld (1-4) -
col: Spaltenposition im Feld (1-4)
Formatierung
Für unsere Analyse sollte gen als Faktor kodiert werden. Für row und col benötigen wir beide sowohl als Integer (für desplot()) als auch als Faktoren (für das statistische Modell). Wir erstellen Faktorversionen mit dem Suffix “F”:
# A tibble: 16 × 6
gen row col yield rowF colF
<fct> <int> <int> <dbl> <fct> <fct>
1 Dasher 1 3 44.2 1 3
2 Dasher 2 4 54.1 2 4
3 Dasher 3 2 47.2 3 2
4 Dasher 4 1 36.7 4 1
5 Guardian 1 4 33 1 4
6 Guardian 2 2 13.6 2 2
7 Guardian 3 1 44.1 3 1
8 Guardian 4 3 35.8 4 3
9 Poinsett 1 1 11.5 1 1
10 Poinsett 2 3 22.4 2 3
11 Poinsett 3 4 30.3 3 4
12 Poinsett 4 2 21.5 4 2
13 Sprint 1 2 15.1 1 2
14 Sprint 2 1 20.3 2 1
15 Sprint 3 3 41.3 3 3
16 Sprint 4 4 27.1 4 4 Erkunden
Betrachten wir die deskriptiven Statistiken nach Genotyp, um die Behandlungseffekte zu verstehen:
# A tibble: 4 × 6
gen count mean_yield sd_yield min_yield max_yield
<fct> <int> <dbl> <dbl> <dbl> <dbl>
1 Dasher 4 45.6 7.21 36.7 54.1
2 Guardian 4 31.6 12.9 13.6 44.1
3 Sprint 4 26.0 11.4 15.1 41.3
4 Poinsett 4 21.4 7.71 11.5 30.3Untersuchen wir nun die Zeilen- und Spalteneffekte, um zu sehen, ob die Blockbildung vorteilhaft war:
# A tibble: 4 × 6
rowF count mean_yield sd_yield min_yield max_yield
<fct> <int> <dbl> <dbl> <dbl> <dbl>
1 3 4 40.7 7.36 30.3 47.2
2 4 4 30.3 7.28 21.5 36.7
3 2 4 27.6 18.1 13.6 54.1
4 1 4 26.0 15.4 11.5 44.2# A tibble: 4 × 6
colF count mean_yield sd_yield min_yield max_yield
<fct> <int> <dbl> <dbl> <dbl> <dbl>
1 4 4 36.1 12.2 27.1 54.1
2 3 4 35.9 9.67 22.4 44.2
3 1 4 28.2 14.9 11.5 44.1
4 2 4 24.4 15.6 13.6 47.2Wir können sehen, dass:
- Der Genotyp Dasher den höchsten mittleren Ertrag hat
- Zeile 3 deutlich höhere Erträge zeigt als andere Zeilen
- Spalte 4 den höchsten mittleren Ertrag hat
Diese systematischen Unterschiede in Zeilen und Spalten bestätigen, dass das Lateinische Quadrat für dieses Experiment geeignet war.
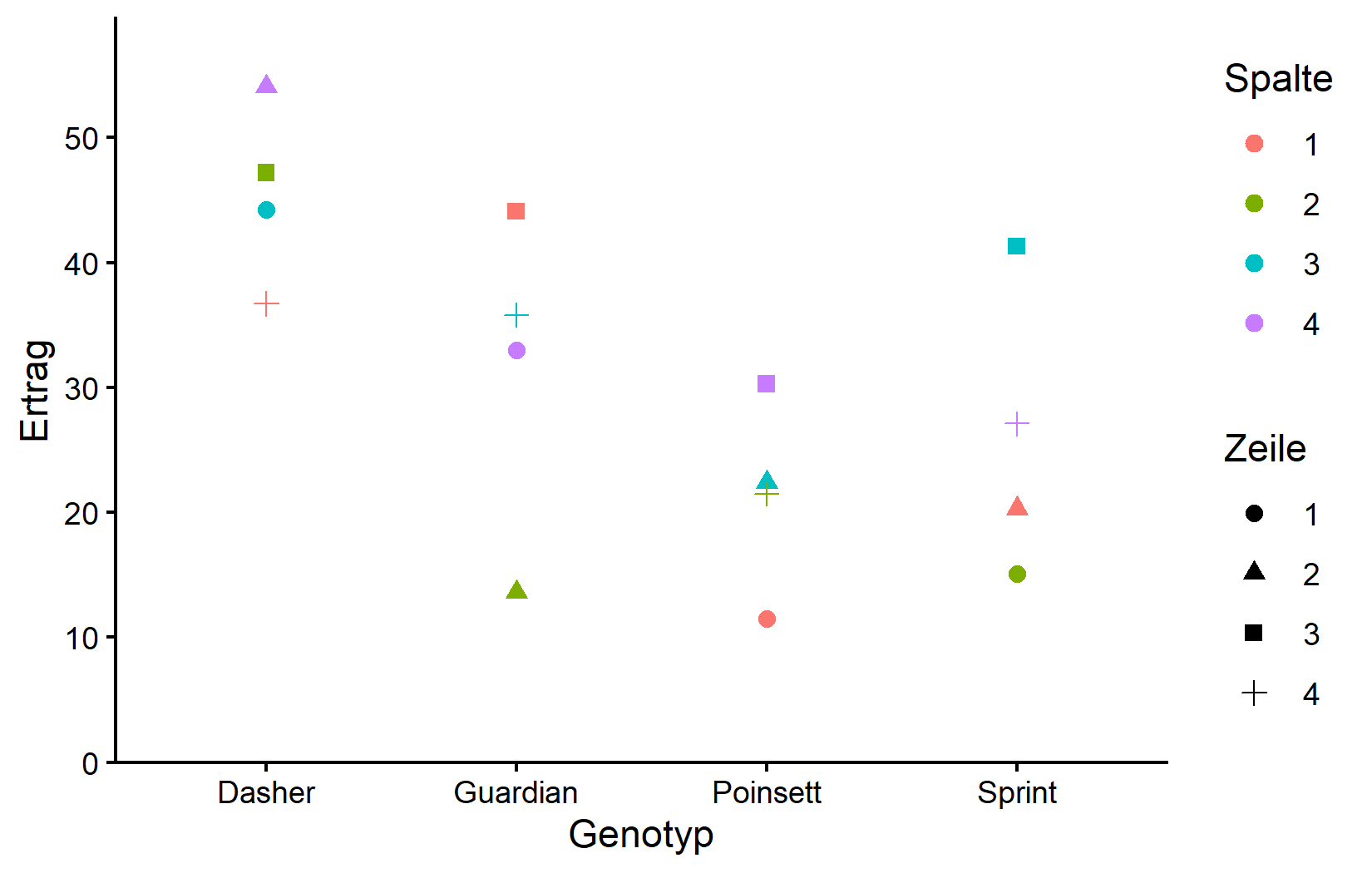
Visualisieren wir die Daten, um die Beziehungen zu verstehen:
ggplot(data = dat) +
aes(y = yield, x = gen, color = colF, shape = rowF) +
geom_point(size = 2) +
scale_x_discrete(
name = "Genotyp"
) +
scale_y_continuous(
name = "Ertrag",
limits = c(0, NA),
expand = expansion(mult = c(0, 0.1))
) +
scale_color_discrete(
name = "Spalte"
) +
scale_shape_discrete(
name = "Zeile"
) +
theme_classic()Diese Darstellung zeigt, wie die Erträge nach Genotyp (x-Achse) variieren, wobei Farben die Spalten und Formen die Zeilen repräsentieren. Beachten Sie, dass innerhalb jedes Genotyps Variation vorhanden ist, die auf Zeilen- und Spaltenpositionen zurückgeführt werden kann.
Visualisieren wir nun das experimentelle Layout, um die Struktur des Lateinischen Quadrats zu verstehen:
desplot(
data = dat,
flip = TRUE, # Zeile 1 oben, nicht unten
form = gen ~ col + row, # Füllfarbe pro Genotyp
out1 = rowF, # Linie zwischen Zeilen
out2 = colF, # Linie zwischen Spalten
out1.gpar = list(col = "black", lwd = 2), # Zeilenlinienstil
out2.gpar = list(col = "black", lwd = 2), # Spaltenlinienstil
text = gen, # Genotypnamen pro Parzelle
cex = 1, # Genotypnamen: Schriftgröße
shorten = FALSE, # Genotypnamen: nicht abkürzen
main = "Feldlayout: Genotypen", # Titel der Darstellung
show.key = FALSE # Legende ausblenden
)desplot(
data = dat,
flip = TRUE, # Zeile 1 oben, nicht unten
form = yield ~ col + row, # Füllfarbe entsprechend dem Ertrag
out1 = rowF, # Linie zwischen Zeilen
out2 = colF, # Linie zwischen Spalten
out1.gpar = list(col = "black", lwd = 2), # Zeilenlinienstil
out2.gpar = list(col = "black", lwd = 2), # Spaltenlinienstil
text = gen, # Genotypnamen pro Parzelle
cex = 1, # Genotypnamen: Schriftgröße
shorten = FALSE, # Genotypnamen: nicht abkürzen
main = "Ertrag pro Parzelle", # Titel der Darstellung
show.key = FALSE # Legende ausblenden
)Die Feldlayouts bestätigen die Struktur des Lateinischen Quadrats:
- Jeder Genotyp erscheint genau einmal in jeder Zeile
- Jeder Genotyp erscheint genau einmal in jeder Spalte
- Zeile 3 zeigt generell höhere Erträge (dunklere Farben in der Ertragsdarstellung)
- Spalte 4 zeigt höhere Erträge
- Dasher tendiert zu hohen Erträgen unabhängig von der Position
Modell und ANOVA
Das Modell des Lateinischen Quadrats verstehen
Das Modell des Lateinischen Quadrats erweitert das RCBD-Modell durch Einbeziehung sowohl von Zeilen- als auch Spalteneffekten. Während ein RCBD nur Behandlungs- und Blockeffekte enthält:
yield ~ genotype + block
enthält das Modell des Lateinischen Quadrats Behandlungs-, Zeilen- und Spalteneffekte:
yield ~ genotype + row + column
Passen wir dieses Modell an:
mod <- lm(yield ~ gen + rowF + colF, data = dat)
mod
Call:
lm(formula = yield ~ gen + rowF + colF, data = dat)
Coefficients:
(Intercept) genGuardian genPoinsett genSprint rowF2 rowF3
37.375 -13.925 -24.125 -19.600 1.650 14.775
rowF4 colF2 colF3 colF4
4.325 -3.800 7.775 7.975 Beachten Sie, dass die Koeffizienten nun Genotyp-, Zeilen- und Spalteneffekte enthalten. Die Zeileneffekte zeigen, dass row3 einen positiven Effekt hat (höhere Erträge), während die Spalteneffekte zeigen, dass col4 den größten positiven Effekt hat. Wie immer wird die erste Stufe jedes Faktors als Referenzniveau gesetzt (Koeffizient = 0).
Es ist entscheidend, rowF und colF (die Faktorversionen) anstelle von row und col im Modell zu verwenden. Faktoren ermöglichen es dem Modell, separate Effekte für jede Zeilen- und Spaltenstufe zu schätzen, während numerische Variablen lineare Trends schätzen würden, die gleiche Abstände zwischen den Stufen annehmen.
An dieser Stelle (d.h. nach dem Modell-Fit und vor der ANOVA-Interpretation) sollte man prüfen, ob die Modellannahmen erfüllt sind. Mehr dazu im Anhang A1: Modelldiagnostik.
Durchführung der ANOVA
ANOVA <- anova(mod)
ANOVAAnalysis of Variance Table
Response: yield
Df Sum Sq Mean Sq F value Pr(>F)
gen 3 1316.80 438.93 9.3683 0.01110 *
rowF 3 528.35 176.12 3.7589 0.07872 .
colF 3 411.16 137.05 2.9252 0.12197
Residuals 6 281.12 46.85
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1In dieser ANOVA-Tabelle:
- Drei Effekte erscheinen:
gen,rowFundcolF - Alle drei Effekte sind statistisch signifikant (p < 0.05)
- Der Genotypeffekt (p < 0.05) zeigt signifikante Unterschiede zwischen den Genotypen an
- Sowohl der Zeilen- (p < 0.05) als auch der Spalteneffekt (p < 0.05) sind signifikant, was bestätigt, dass das Lateinische Quadrat vorteilhaft war
Die signifikanten Zeilen- und Spalteneffekte validieren unsere Entscheidung, ein Lateinisches Quadrat zu verwenden. Durch die Einbeziehung dieser Effekte in unser Modell haben wir systematische Variation berücksichtigt, die sonst zum Versuchsfehler beigetragen hätte, wodurch die Präzision unserer Genotypvergleiche erhöht wurde.
Mittelwertvergleiche
Nun können wir mit Post-hoc-Vergleichen fortfahren, um zu identifizieren, welche Genotypen sich signifikant voneinander unterscheiden. Wie bei unseren vorherigen Analysen verwenden wir geschätzte Randmittelwerte (emmeans):
gen emmean SE df lower.CL upper.CL .group
Poinsett 21.4 3.42 6 9.43 33.4 a
Sprint 25.9 3.42 6 13.95 37.9 a
Guardian 31.6 3.42 6 19.63 43.6 ab
Dasher 45.5 3.42 6 33.55 57.5 b
Results are averaged over the levels of: rowF, colF
Confidence level used: 0.95
Conf-level adjustment: sidak method for 4 estimates
P value adjustment: tukey method for comparing a family of 4 estimates
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Diese Mittelwerte sind für sowohl Zeilen- als auch Spalteneffekte adjustiert. In einem balancierten Lateinischen Quadrat wie diesem sind die adjustierten Mittelwerte die Genotypdurchschnitte über alle Zeilen-Spalten-Kombinationen, aber der emmeans-Ansatz berücksichtigt die experimentelle Struktur ordnungsgemäß bei der Berechnung von Standardfehlern und Konfidenzintervallen.
Die Kompaktbuchstabendarstellung zeigt, dass Dasher (Gruppe “b”) einen signifikant höheren Ertrag hat als die anderen drei Genotypen (Gruppe “a”), die sich nicht signifikant voneinander unterscheiden.
Visualisierung der Ergebnisse
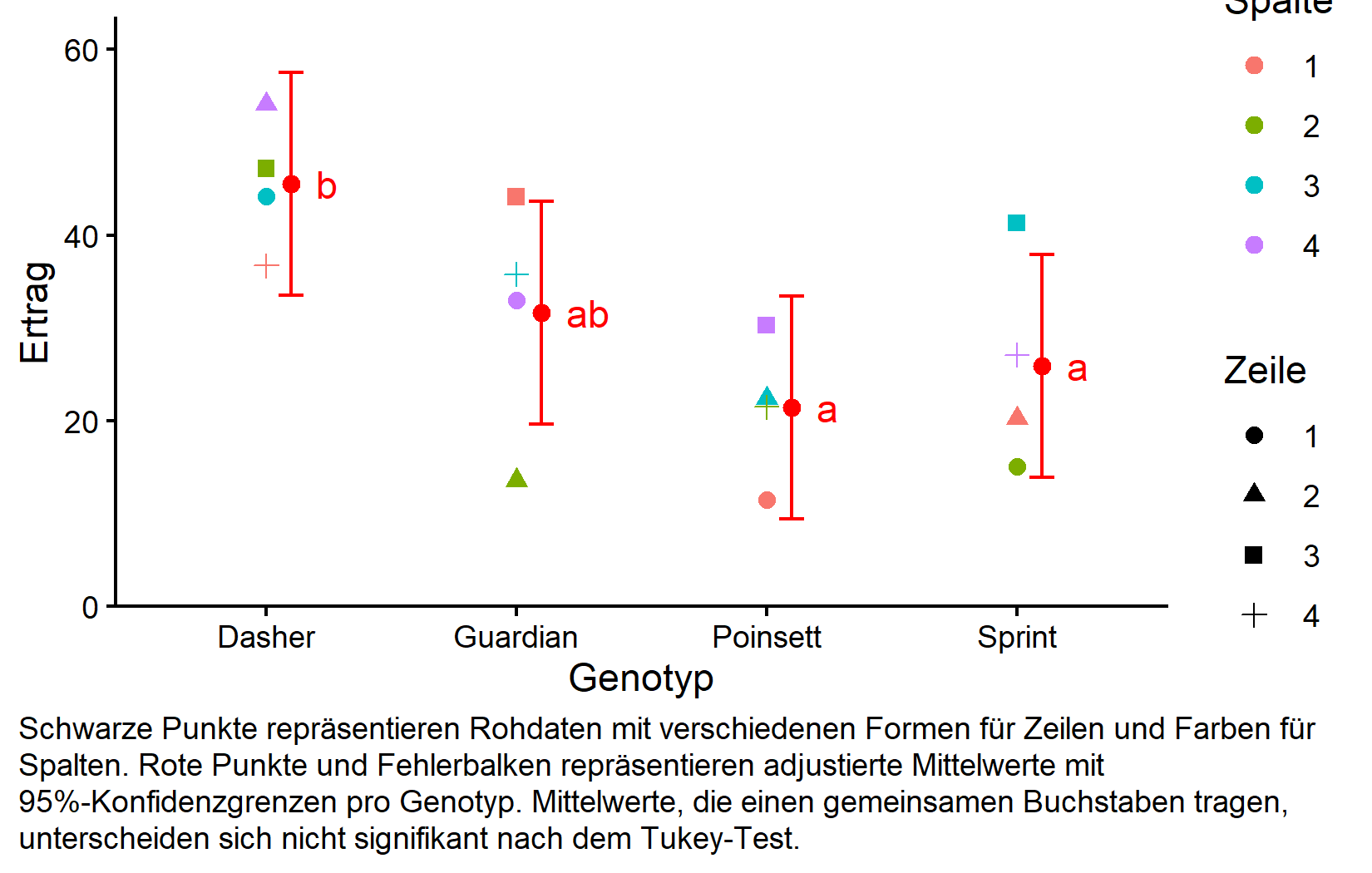
Abschließend erstellen wir eine umfassende Darstellung, die sowohl die Rohdaten als auch unsere statistischen Ergebnisse zeigt:
my_caption <- "Schwarze Punkte repräsentieren Rohdaten mit verschiedenen Formen für Zeilen und Farben für Spalten. Rote Punkte und Fehlerbalken repräsentieren adjustierte Mittelwerte mit 95%-Konfidenzgrenzen pro Genotyp. Mittelwerte, die einen gemeinsamen Buchstaben tragen, unterscheiden sich nicht signifikant nach dem Tukey-Test."
ggplot() +
aes(x = gen) +
# schwarze Punkte für die Rohdaten
geom_point(
data = dat,
aes(y = yield, shape = rowF, color = colF),
size = 2
) +
# rote Punkte für die adjustierten Mittelwerte
geom_point(
data = mean_comp,
aes(y = emmean),
color = "red",
position = position_nudge(x = 0.1),
size = 2
) +
# rote Fehlerbalken für die Konfidenzgrenzen der adjustierten Mittelwerte
geom_errorbar(
data = mean_comp,
aes(ymin = lower.CL, ymax = upper.CL),
color = "red",
width = 0.1,
position = position_nudge(x = 0.1)
) +
# rote Buchstaben
geom_text(
data = mean_comp,
aes(y = emmean, label = str_trim(.group)),
color = "red",
position = position_nudge(x = 0.2),
hjust = 0
) +
scale_x_discrete(
name = "Genotyp"
) +
scale_y_continuous(
name = "Ertrag",
limits = c(0, NA),
expand = expansion(mult = c(0, 0.1))
) +
scale_color_discrete(
name = "Spalte"
) +
scale_shape_discrete(
name = "Zeile"
) +
theme_classic() +
labs(caption = my_caption) +
theme(plot.caption = element_textbox_simple(margin = margin(t = 5)),
plot.caption.position = "plot")Diese Darstellung zeigt effektiv sowohl die experimentelle Designstruktur (durch die verschiedenen Formen und Farben, die Zeilen- und Spaltenpositionen repräsentieren) als auch die statistischen Ergebnisse (durch die roten Punkte, die adjustierte Mittelwerte zeigen, und Buchstaben, die Signifikanzgruppen zeigen).
Zusammenfassung des Designvergleichs
Fassen wir die Progression von CRD über RCBD zum Lateinischen Quadrat zusammen:
-
Modellformeln:
- CRD:
yield ~ genotype - RCBD:
yield ~ genotype + block - Lateinisches Quadrat:
yield ~ genotype + row + column
- CRD:
-
Kontrollierte Variationsquellen:
- CRD: Keine (Behandlungen vs. Restfehler)
- RCBD: Eine (Behandlungen, Blöcke vs. Restfehler)
- Lateinisches Quadrat: Zwei (Behandlungen, Zeilen, Spalten vs. Restfehler)
-
Designanforderungen:
- CRD: Zufällige Zuweisung von Behandlungen zu Versuchseinheiten
- RCBD: Jede Behandlung erscheint einmal pro Block
- Lateinisches Quadrat: Jede Behandlung erscheint einmal pro Zeile UND einmal pro Spalte
-
Wann zu verwenden:
- CRD: Wenn Versuchseinheiten homogen sind
- RCBD: Wenn eine Quelle systematischer Variation existiert
- Lateinisches Quadrat: Wenn zwei Quellen systematischer Variation existieren und die Anzahl der Behandlungen klein ist (3-6)
Zusammenfassung
Sie haben nun gelernt, wie man Daten aus einem Lateinischen Quadrat analysiert, das das Blockbildungsprinzip erweitert, um zwei Quellen systematischer Variation gleichzeitig zu kontrollieren. Dieses spezialisierte Design bietet erhöhte Präzision, wenn sowohl Zeilen- als auch Spalteneffekte vorhanden sind und die Designannahmen erfüllt sind.
Das Lateinische Quadrat kontrolliert zwei Quellen systematischer Variation, indem sichergestellt wird, dass jede Behandlung genau einmal in jeder Zeile und jeder Spalte erscheint.
Erhöhte Präzision kann durch Entfernung sowohl von Zeilen- als auch Spalteneffekten aus dem Versuchsfehler erreicht werden, vorausgesetzt es gibt keine Zeile × Spalte Interaktionen.
Das Modell des Lateinischen Quadrats enthält Behandlungs-, Zeilen- und Spalteneffekte:
response ~ treatment + row + column.Designeinschränkungen erfordern gleiche Anzahlen von Behandlungen, Zeilen und Spalten, was es am praktischsten für 3-6 Behandlungen macht.
Kritische Annahme: Das Design nimmt keine Interaktion zwischen Zeilen- und Spalteneffekten an. Eine Verletzung dieser Annahme kann das Design weniger effizient als Alternativen machen.
Die ANOVA für das Lateinische Quadrat testet Behandlungs-, Zeilen- und Spalteneffekte - signifikante Zeilen- und Spalteneffekte bestätigen, dass das Design vorteilhaft war.
Wann zu vermeiden: Lateinische Quadrate sind nicht geeignet, wenn Behandlungszahlen groß sind (>6), Zeile × Spalte Interaktionen erwartet werden, oder wenn andere Designs besser zu den experimentellen Zielen passen.
Literatur
Zitat
@online{schmidt2026,
author = {{Dr. Paul Schmidt}},
publisher = {BioMath GmbH},
title = {3. Einfaktorielle ANOVA im Lateinischen Quadrat},
date = {2026-02-08},
url = {https://biomathcontent.netlify.app/de/content/lin_mod_exp/03_oneway_latinsquare.html},
langid = {de}
}