6. Einfaktorielle ANOVA im Zeilen-Spalten-Design

Varianzanalyse (ANOVA); Auflosbares Zeilen-Spalten-Design

Author
Zugehörigkeit

Dr. Paul Schmidt

BioMath GmbH

Last updated

8. Februar 2026

Um alle in diesem Kapitel verwendeten Pakete zu installieren und zu laden, führen Sie folgenden Code aus:

for (pkg in c("agridat", "desplot", "emmeans", "ggtext", "here", "lme4", 
              "lmerTest", "multcomp", "multcompView", "tidyverse")) {
  if (!require(pkg, character.only = TRUE)) install.packages(pkg)
}

library(agridat)
library(desplot)
library(emmeans)
library(ggtext)
library(here)
library(lme4)
library(lmerTest)
library(multcomp)
library(multcompView)
library(tidyverse)

Zeilen-Spalten-Designs

In Kapitel 3 haben wir das Lateinische Quadrat kennengelernt, das zwei Variationsquellen (Zeilen und Spalten) gleichzeitig kontrolliert. Das Lateinische Quadrat hat jedoch eine wesentliche Einschränkung: Die Anzahl der Behandlungen muss gleich der Anzahl der Zeilen und Spalten sein. Dies macht es für Experimente mit vielen Behandlungen unpraktisch.

Was ist ein Zeilen-Spalten-Design?

Ein auflösbares Zeilen-Spalten-Design erweitert das Konzept des Lateinischen Quadrats, um mehr Behandlungen aufzunehmen. Wie ein Alpha-Design hat es vollständige Wiederholungen, die unterteilt sind - aber hier ist jede Wiederholung sowohl in unvollständige Zeilen als auch in unvollständige Spalten unterteilt. Dies bietet eine doppelte Blockbildung innerhalb jeder Wiederholung.

Die wesentlichen Merkmale sind:

  1. Zweidimensionale Blockbildung: Jede Wiederholung hat sowohl Zeilen- als auch Spaltenstruktur
  2. Unvollständige Blöcke: Weder Zeilen noch Spalten enthalten alle Behandlungen
  3. Auflösbarkeit: Wiederholungen sind vollständig und enthalten jede Behandlung genau einmal
  4. Flexibilität: Kann verschiedene Anzahlen von Behandlungen aufnehmen

Die Vorteile umfassen:

  1. Kontrolle von zwei Gradienten: Berücksichtigt räumliche Trends in zwei Richtungen gleichzeitig
  2. Mehr Behandlungen als Lateinisches Quadrat: Nicht auf t×t-Anordnungen beschränkt
  3. Erhöhte Präzision: Doppelte Blockbildung kann den Versuchsfehler erheblich reduzieren
  4. Praktisch für Feldversuche: Passt zum rechteckigen Layout vieler Feldexperimente

Daten

Dieses Beispiel betrachtet Daten, die in Kempton, Fox, und Cerezo (1997) veröffentlicht wurden, aus einem Ertragsversuch, der als auflösbares Zeilen-Spalten-Design angelegt wurde. Der Versuch hatte 35 Genotypen (gen), 2 vollständige Wiederholungen (rep) mit jeweils 5 Zeilen (row) und 7 Spalten (col). Somit bildet jede Wiederholung ein 5×7-Raster mit unvollständigen Zeilen und Spalten.

Import

Die Daten sind als Teil des {agridat}-Pakets verfügbar:

dat <- as_tibble(agridat::kempton.rowcol)
dat
# A tibble: 68 × 5
   rep     row   col gen   yield
   <fct> <int> <int> <fct> <dbl>
 1 R1        1     1 G20    3.77
 2 R1        1     2 G04    3.21
 3 R1        1     3 G33    4.55
 4 R1        1     4 G28    4.09
 5 R1        1     5 G07    5.05
 6 R1        1     6 G12    4.19
 7 R1        1     7 G30    3.27
 8 R1        2     1 G10    3.44
 9 R1        2     2 G14    4.3 
10 R1        2     4 G21    3.86
# ℹ 58 more rows

Der Datensatz enthält:

  • rep: Zwei vollständige Wiederholungen (R1, R2)
  • row: Zeilenposition innerhalb der Wiederholung (1-5)
  • col: Spaltenposition innerhalb der Wiederholung (1-7)
  • gen: 35 Genotypen
  • yield: Ernteertrag

Beachten Sie, dass in diesem Datensatz fehlende Werte vorhanden sind - zwei Parzellen haben keinen erfassten Ertrag.

Formatierung

Für unsere Analyse sollte gen als Faktor kodiert werden. Wir erstellen auch Faktorversionen von row und col für das statistische Modell:

dat <- dat %>%
  mutate(
    gen = as.factor(gen),
    rowF = as.factor(row),
    colF = as.factor(col)
  )

dat
# A tibble: 68 × 7
   rep     row   col gen   yield rowF  colF 
   <fct> <int> <int> <fct> <dbl> <fct> <fct>
 1 R1        1     1 G20    3.77 1     1    
 2 R1        1     2 G04    3.21 1     2    
 3 R1        1     3 G33    4.55 1     3    
 4 R1        1     4 G28    4.09 1     4    
 5 R1        1     5 G07    5.05 1     5    
 6 R1        1     6 G12    4.19 1     6    
 7 R1        1     7 G30    3.27 1     7    
 8 R1        2     1 G10    3.44 2     1    
 9 R1        2     2 G14    4.3  2     2    
10 R1        2     4 G21    3.86 2     4    
# ℹ 58 more rows

Erkunden

Betrachten wir die deskriptiven Statistiken nach Genotyp:

dat %>% 
  group_by(gen) %>% 
  summarize(
    count = n(),
    mean_yield = mean(yield, na.rm = TRUE),
    sd_yield = sd(yield, na.rm = TRUE)
  ) %>%
  arrange(desc(mean_yield))
# A tibble: 35 × 4
   gen   count mean_yield sd_yield
   <fct> <int>      <dbl>    <dbl>
 1 G19       2       6.07   1.84  
 2 G07       2       5.74   0.976 
 3 G33       2       5.13   0.820 
 4 G06       2       4.96   0.940 
 5 G09       2       4.94   1.68  
 6 G11       2       4.93   1.03  
 7 G14       2       4.92   0.877 
 8 G27       2       4.89   1.80  
 9 G03       2       4.78   0.0424
10 G25       2       4.78   0.361 
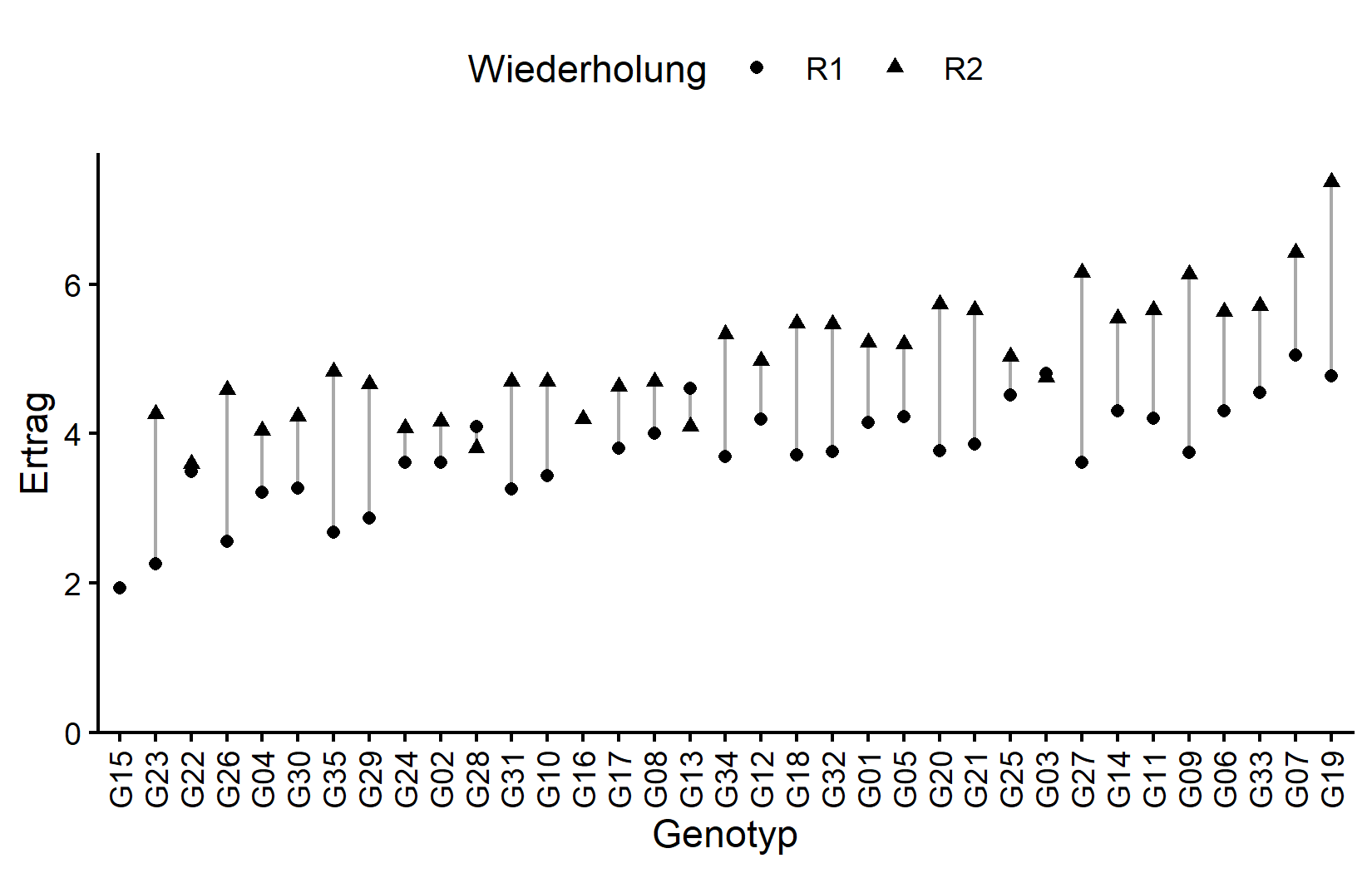
# ℹ 25 more rows

Die meisten Genotypen erscheinen zweimal (einmal pro Wiederholung), aber einige haben aufgrund fehlender Daten nur eine Beobachtung. Visualisieren wir die Daten:

# Genotypen nach mittlerem Ertrag sortieren
gen_order <- dat %>% 
  group_by(gen) %>% 
  summarise(mean = mean(yield, na.rm = TRUE)) %>% 
  arrange(mean) %>% 
  pull(gen) %>% 
  as.character()

ggplot(data = dat) +
  aes(
    y = yield,
    x = gen,
    shape = rep
  ) +
  geom_line(
    aes(group = gen),
    color = "darkgrey"
  ) +
  geom_point() +
  scale_x_discrete(
    name = "Genotyp",
    limits = gen_order
  ) +
  scale_y_continuous(
    name = "Ertrag",
    limits = c(0, NA),
    expand = expansion(mult = c(0, 0.05))
  ) +
  scale_shape_discrete(
    name = "Wiederholung"
  ) +
  guides(shape = guide_legend(nrow = 1)) +
  theme_classic() +
  theme(
    legend.position = "top", 
    axis.text.x = element_text(angle = 90, vjust = 0.5)
  )

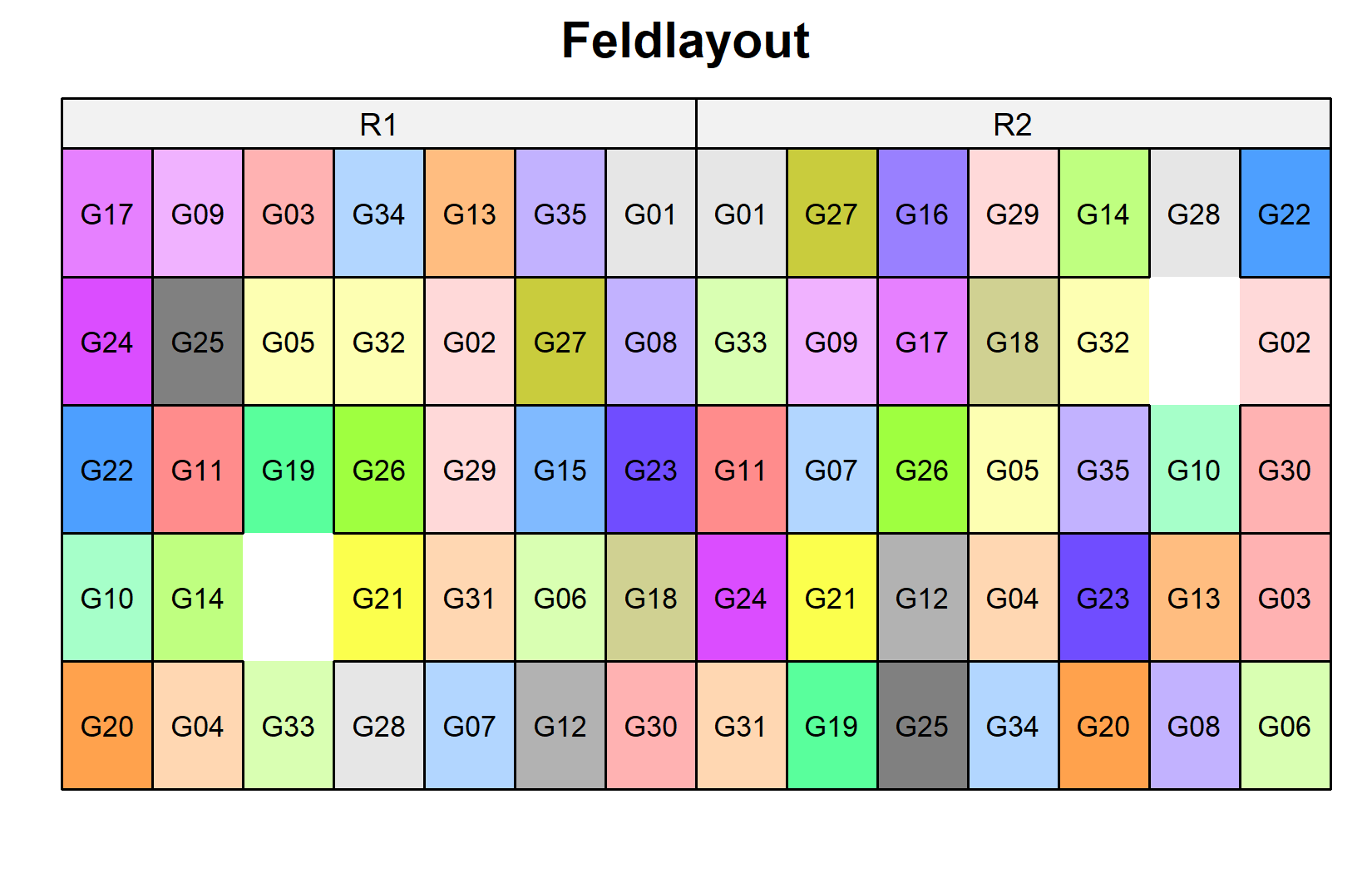
Schauen wir uns nun das Feldlayout an. Beachten Sie, dass die zwei fehlenden Parzellen als weiß/leer erscheinen:

desplot(
  data = dat,
  form = gen ~ col + row | rep, # Füllfarbe pro Genotyp, Panels pro Wiederholung
  text = gen, 
  cex = 0.7, 
  shorten = FALSE,
  out1 = row, out1.gpar = list(col = "black"), # Linien zwischen Zeilen
  out2 = col, out2.gpar = list(col = "black"), # Linien zwischen Spalten
  main = "Feldlayout", 
  show.key = FALSE
)

Die schwarzen Linien zeigen die Zeilen- und Spaltenstruktur innerhalb jeder Wiederholung. Jeder Genotyp erscheint einmal pro Wiederholung, aber in verschiedenen Zeilen-Spalten-Positionen.

Modell und ANOVA

Wahl zwischen festen und zufaelligen Effekten

Für ein Zeilen-Spalten-Design muss das Modell Zeilen- und Spalteneffekte innerhalb jeder Wiederholung berücksichtigen. Wir können diese als feste oder zufällige Effekte behandeln. Vergleichen wir beide Ansätze:

# Zeilen und Spalten als feste Effekte
mod_fixed <- lm(yield ~ gen + rep + rep:rowF + rep:colF,
                data = dat)

# Zeilen und Spalten als zufällige Effekte
mod_random <- lmer(yield ~ gen + rep + (1 | rep:rowF) + (1 | rep:colF),
                   data = dat)

Vergleichen wir nun den durchschnittlichen s.e.d. für Genotypvergleiche:

# s.e.d. für festes Modell
sed_fixed <- mod_fixed %>%
  emmeans(pairwise ~ "gen", adjust = "none") %>%
  pluck("contrasts") %>%
  as_tibble() %>%
  pull("SE") %>%
  mean()
NOTE: A nesting structure was detected in the fitted model:
    rowF %in% rep, colF %in% rep
# s.e.d. für zufälliges Modell  
sed_random <- mod_random %>%
  emmeans(pairwise ~ "gen", adjust = "none", lmer.df = "kenward-roger") %>%
  pluck("contrasts") %>%
  as_tibble() %>%
  pull("SE") %>%
  mean()

tibble(
  model = c("Feste Zeilen/Spalten", "Zufällige Zeilen/Spalten"),
  mean_sed = c(sed_fixed, sed_random)
)
# A tibble: 2 × 2
  model                    mean_sed
  <chr>                       <dbl>
1 Feste Zeilen/Spalten        0.408
2 Zufällige Zeilen/Spalten    0.402

In diesem Fall hat das Modell mit festen Effekten einen etwas kleineren s.e.d., daher verwenden wir es für unsere Analyse.

An dieser Stelle (d.h. nach dem Modell-Fit und vor der ANOVA-Interpretation) sollte man prüfen, ob die Modellannahmen erfüllt sind. Mehr dazu im Anhang A1: Modelldiagnostik.

Durchführung der ANOVA

ANOVA <- anova(mod_fixed)
ANOVA
Analysis of Variance Table

Response: yield
          Df Sum Sq Mean Sq  F value    Pr(>F)    
gen       34 32.157  0.9458  10.7456 4.969e-05 ***
rep        1 24.901 24.9014 282.9193 1.042e-09 ***
rep:rowF   8  2.512  0.3140   3.5680  0.023647 *  
rep:colF  12  6.327  0.5273   5.9905  0.002067 ** 
Residuals 12  1.056  0.0880                       
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Der Genotypeffekt ist nicht statistisch signifikant (p > 0.05), was auf keine starke Evidenz für Unterschiede zwischen Genotypen in diesem Versuch hinweist. Dennoch untersuchen wir die Mittelwertvergleiche.

Mittelwertvergleiche

mean_comp <- mod_fixed %>% 
  emmeans(specs = ~ gen) %>%
  cld(adjust = "none", Letters = letters)

mean_comp
 gen emmean    SE df lower.CL upper.CL .group       
 G04   3.48 0.270 12     2.89     4.07  a           
 G23   3.58 0.270 12     2.99     4.17  ab          
 G15   3.60 0.442 12     2.64     4.57  abcde       
 G35   3.63 0.277 12     3.03     4.24  abc         
 G31   3.79 0.280 12     3.18     4.40  abcd        
 G02   3.84 0.279 12     3.23     4.45  abcd        
 G26   3.90 0.291 12     3.26     4.53  abcde       
 G24   3.90 0.267 12     3.32     4.49  abcd f      
 G29   3.91 0.276 12     3.31     4.51  abcde       
 G30   3.99 0.270 12     3.40     4.58  abcdefg     
 G32   4.12 0.276 12     3.52     4.72  abcdefgh    
 G17   4.14 0.282 12     3.53     4.75  abcdefgh    
 G09   4.15 0.274 12     3.56     4.75  abcdefgh    
 G34   4.20 0.267 12     3.62     4.78  abcdefgh    
 G16   4.23 0.432 12     3.29     5.17  abcdefghij  
 G05   4.25 0.278 12     3.64     4.85  abcdefghi   
 G20   4.25 0.266 12     3.67     4.83  abcdefgh    
 G22   4.27 0.282 12     3.66     4.88  abcdefghi   
 G10   4.36 0.278 12     3.76     4.97  abcdefghij  
 G28   4.37 0.278 12     3.77     4.98   bcdefghij  
 G18   4.48 0.284 12     3.86     5.10    cdefghij  
 G21   4.57 0.269 12     3.98     5.16     defghij  
 G08   4.58 0.285 12     3.95     5.20     defghij  
 G25   4.59 0.277 12     3.98     5.19     defghij  
 G13   4.73 0.284 12     4.11     5.35      e ghijkl
 G27   4.75 0.282 12     4.13     5.36       fghijk 
 G33   4.76 0.286 12     4.13     5.38      e ghijk 
 G14   4.79 0.270 12     4.20     5.38        ghijkl
 G01   4.88 0.268 12     4.30     5.46         hijkl
 G07   4.94 0.270 12     4.35     5.53         hijkl
 G11   4.97 0.276 12     4.37     5.57         hijkl
 G12   5.13 0.293 12     4.49     5.77          ijkl
 G03   5.15 0.281 12     4.54     5.76           jkl
 G06   5.53 0.280 12     4.92     6.14            kl
 G19   5.60 0.281 12     4.99     6.22             l

Results are averaged over the levels of: colF, rowF, rep 
Confidence level used: 0.95 
significance level used: alpha = 0.05 
NOTE: If two or more means share the same grouping symbol,
      then we cannot show them to be different.
      But we also did not show them to be the same.

Die Kompaktbuchstabendarstellung zeigt die Gruppierungen basierend auf Fishers LSD-Test. Bei 35 Genotypen wird die Buchstabendarstellung komplex, bietet aber dennoch eine prägnante Zusammenfassung, welche Genotypen sich signifikant unterscheiden.

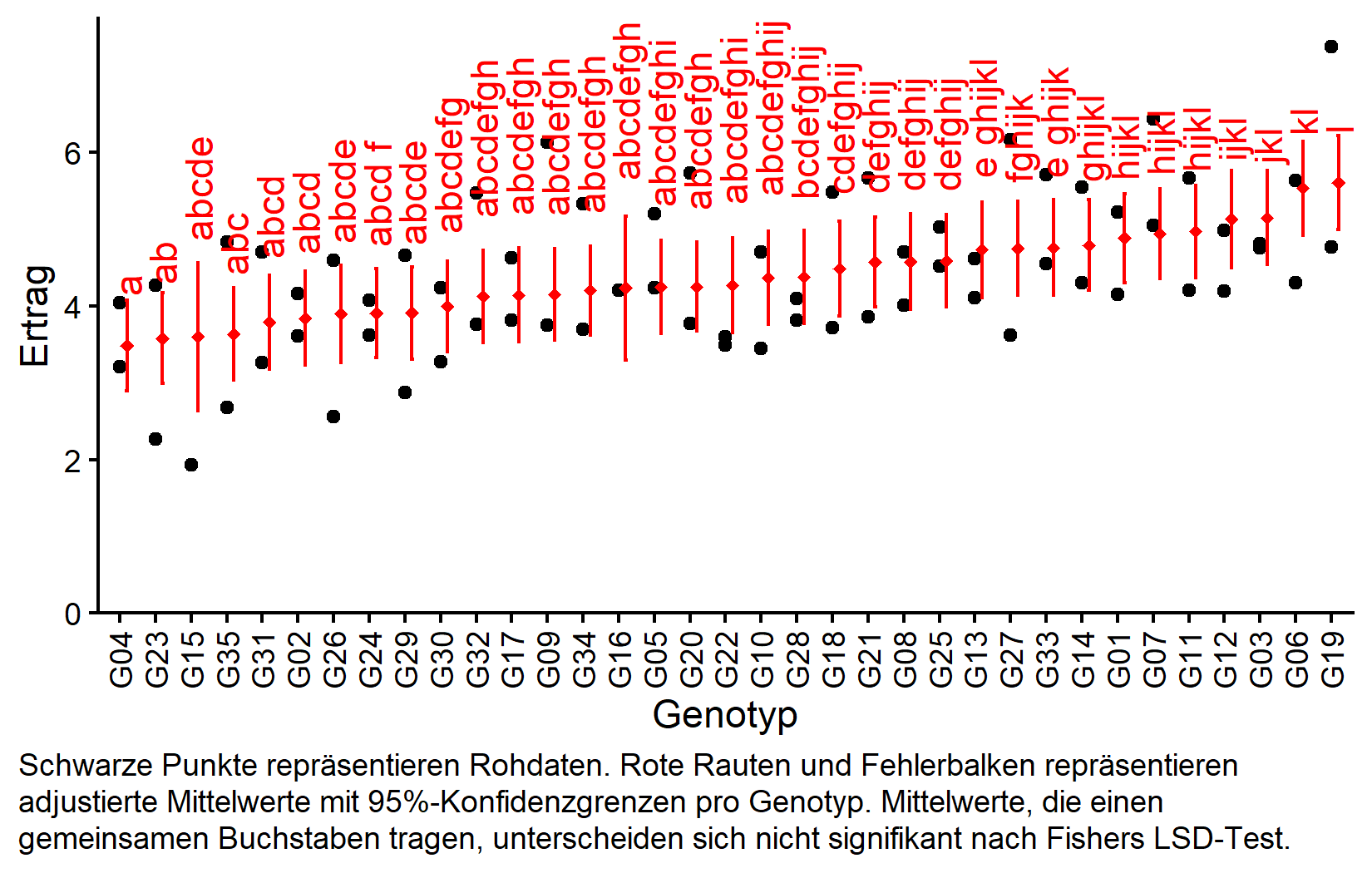
Visualisierung der Ergebnisse

my_caption <- "Schwarze Punkte repräsentieren Rohdaten. Rote Rauten und Fehlerbalken repräsentieren adjustierte Mittelwerte mit 95%-Konfidenzgrenzen pro Genotyp. Mittelwerte, die einen gemeinsamen Buchstaben tragen, unterscheiden sich nicht signifikant nach Fishers LSD-Test."

ggplot() +
  aes(x = gen) +
  # schwarze Punkte für die Rohdaten
  geom_point(
    data = dat,
    aes(y = yield)
  ) +
  # rote Rauten für die adjustierten Mittelwerte
  geom_point(
    data = mean_comp,
    aes(y = emmean),
    shape = 18,
    color = "red",
    position = position_nudge(x = 0.2)
  ) +
  # rote Fehlerbalken für die Konfidenzgrenzen der adjustierten Mittelwerte
  geom_errorbar(
    data = mean_comp,
    aes(ymin = lower.CL, ymax = upper.CL),
    color = "red",
    width = 0.1,
    position = position_nudge(x = 0.2)
  ) +
  # rote Buchstaben 
  geom_text(
    data = mean_comp,
    aes(y = upper.CL, label = str_trim(.group)),
    color = "red",
    angle = 90,
    hjust = -0.2,
    position = position_nudge(x = 0.2)
  ) + 
  scale_x_discrete(
    name = "Genotyp",
    limits = as.character(mean_comp$gen)
  ) +
  scale_y_continuous(
    name = "Ertrag",
    expand = expansion(mult = c(0, 0.05))
  ) +
  coord_cartesian(ylim = c(0, NA)) +
  labs(caption = my_caption) +
  theme_classic() +
  theme(plot.caption = element_textbox_simple(margin = margin(t = 5)),
        plot.caption.position = "plot",
        axis.text.x = element_text(angle = 90, vjust = 0.5))

Bonus: Designeffizienz

Bewerten wir die Effizienz des Zeilen-Spalten-Designs im Vergleich zu einem einfachen RCBD (unter Ignorierung der Zeilen- und Spaltenstruktur):

# s.e.d. quadriert für RCBD (unter Ignorierung der Zeilen-/Spaltenstruktur)
avg_sed_rcbd <- lm(yield ~ gen + rep, data = dat) %>% 
  emmeans(pairwise ~ "gen", adjust = "none") %>%
  pluck("contrasts") %>%
  as_tibble() %>%
  pull("SE") %>%
  mean()

# Effizienz
avg_sed_rcbd^2 / sed_fixed^2
[1] 1.953932

Eine Effizienz > 1 zeigt an, dass das Zeilen-Spalten-Design effizienter ist als ein einfaches RCBD, was bedeutet, dass die Zeilen- und Spaltenblockierung den Versuchsfehler erfolgreich reduziert hat.

Zusammenfassung

Sie haben nun gelernt, wie man Daten aus einem auflösbaren Zeilen-Spalten-Design analysiert, das eine leistungsstarke Kontrolle über zwei Quellen räumlicher Variation bietet.

HinweisWichtige Erkenntnisse

  1. Zeilen-Spalten-Designs kontrollieren zwei Variationsquellen gleichzeitig durch Blockbildung sowohl in Zeilen- als auch in Spaltenrichtung innerhalb jeder Wiederholung.

  2. Flexibler als das Lateinische Quadrat: Kann jede Anzahl von Behandlungen aufnehmen, nicht auf t×t-Anordnungen beschränkt.

  3. Doppelte Blockbildung innerhalb von Wiederholungen bietet erhöhte Präzision, wenn räumliche Trends in zwei Richtungen existieren.

  4. Die Modellwahl zwischen festen und zufälligen Zeilen-/Spalteneffekten kann darauf basieren, welche den kleineren durchschnittlichen s.e.d. ergibt.

  5. Das Modell mit festen Effekten: yield ~ gen + rep + rep:rowF + rep:colF (Zeilen und Spalten genestelt innerhalb von Wiederholungen).

  6. Eine Designeffizienz > 1 im Vergleich zum RCBD bestätigt den Vorteil der zusätzlichen Zeilen-Spalten-Struktur.

  7. Umgang mit fehlenden Daten: Zeilen-Spalten-Designs können auch bei fehlenden Beobachtungen analysiert werden, obwohl die Präzision beeinträchtigt sein kann.

Zusammenfassung des Designvergleichs

Fassen wir die Progression der in dieser Kapitelserie behandelten Designs zusammen:

Design Blockstruktur Modellformel Geeignet für
CRD Keine y ~ trt Homogene Bedingungen
RCBD Vollständige Blöcke y ~ trt + block Ein Gradient
Lateinisches Quadrat Zeilen + Spalten (vollständig) y ~ trt + row + col Zwei Gradienten, wenige Behandlungen
Alpha-Design Unvollständige Blöcke in Wdh. y ~ trt + rep + (1|rep:block) Viele Behandlungen, ein Gradient
Augmented Standards + Einträge y ~ trt + block Screening vieler nicht replizierter Einträge
Zeilen-Spalten Unv. Zeilen + Spalten in Wdh. y ~ trt + rep + rep:row + rep:col Viele Behandlungen, zwei Gradienten

Literatur

Kempton, R. A., P. N. Fox, und M. Cerezo. 1997. Statistical Methods for Plant Variety Evaluation. Springer Netherlands. https://doi.org/10.1007/978-94-009-1503-9.

Zitat

Mit BibTeX zitieren:
@online{schmidt2026,
  author = {{Dr. Paul Schmidt}},
  publisher = {BioMath GmbH},
  title = {6. Einfaktorielle ANOVA im Zeilen-Spalten-Design},
  date = {2026-02-08},
  url = {https://biomathcontent.netlify.app/de/content/lin_mod_exp/06_oneway_rowcol.html},
  langid = {de}
}
Bitte zitieren Sie diese Arbeit als:
Dr. Paul Schmidt. 2026. “6. Einfaktorielle ANOVA im Zeilen-Spalten-Design.” BioMath GmbH. February 8, 2026. https://biomathcontent.netlify.app/de/content/lin_mod_exp/06_oneway_rowcol.html.