4. Einfaktorielle ANOVA im Alpha-Design

Um alle in diesem Kapitel verwendeten Pakete zu installieren und zu laden, führen Sie folgenden Code aus:

for (pkg in c("agridat", "desplot", "emmeans", "ggtext", "here", "lme4", 
              "lmerTest", "multcomp", "multcompView", "tidyverse")) {
  if (!require(pkg, character.only = TRUE)) install.packages(pkg)
}

library(agridat)
library(desplot)
library(emmeans)
library(ggtext)
library(here)
library(lme4)
library(lmerTest)
library(multcomp)
library(multcompView)
library(tidyverse)

Von vollstaendigen zu unvollstaendigen Bloecken

In den vorherigen Kapiteln haben wir Daten aus Designs analysiert, bei denen jeder Block alle Behandlungen enthielt: Das RCBD hatte jede Sorte einmal pro Block, und das Lateinische Quadrat hatte jede Behandlung einmal pro Zeile und einmal pro Spalte. Diese werden vollständige Blockdesigns genannt.

Wenn jedoch die Anzahl der Behandlungen groß wird, ist es möglicherweise nicht praktisch oder sogar unmöglich, alle Behandlungen in einen einzelnen Block zu packen. Wenn wir beispielsweise 24 Genotypen haben und unsere Feldparzellen aufgrund von Bodenheterogenitätsbeschränkungen nur 4 Parzellen pro Block aufnehmen können, können wir kein vollständiges Blockdesign verwenden. Hier kommen unvollständige Blockdesigns ins Spiel.

Was ist ein Alpha-Design?

Ein Alpha-Design (auch α-Design genannt) ist eine Art auflösbares unvollständiges Blockdesign. “Auflösbar” bedeutet, dass die unvollständigen Blöcke zu vollständigen Wiederholungen gruppiert werden können, wobei jede Wiederholung jede Behandlung genau einmal enthält. Innerhalb jeder Wiederholung werden die Behandlungen auf mehrere kleinere unvollständige Blöcke verteilt.

Die Vorteile von Alpha-Designs umfassen:

1. Viele Behandlungen handhaben: Praktisch, wenn vollständige Blöcke zu groß wären
2. Lokale Fehlerkontrolle: Kleinere Blöcke sind homogener und reduzieren den Versuchsfehler
3. Auflösbarkeit: Vollständige Wiederholungen ermöglichen eine traditionelle wiederholungsbasierte Analyse als Fallback
4. Flexibilität: Kann verschiedene Anzahlen von Behandlungen und Blockgrößen aufnehmen

Einführung in Gemischte Modelle

In den vorherigen Kapiteln haben wir lm() verwendet, um unsere Modelle anzupassen, wobei alle Effekte als fest behandelt wurden. Für unvollständige Blockdesigns verwenden wir typischerweise gemischte Modelle, die sowohl feste Effekte (wie unseren Behandlungs-/Genotypeffekt) als auch zufällige Effekte (wie unvollständige Blockeffekte) enthalten. Wir verwenden die lmer()-Funktion aus dem {lmerTest}-Paket, um gemischte Modelle anzupassen, wobei zufällige Effekte mit (1 | factor) anstelle von + factor spezifiziert werden.

Daten

Dieses Beispiel betrachtet Daten, die in John und Williams (1995) veröffentlicht wurden, aus einem Ertragsversuch (t/ha), der als Alpha-Design angelegt wurde. Der Versuch hatte 24 Genotypen (gen), 3 vollständige Wiederholungen (rep) und 6 unvollständige Blöcke (block) innerhalb jeder Wiederholung. Die Blockgröße war 4, was bedeutet, dass jeder unvollständige Block 4 der 24 Genotypen enthielt.

Import

Die Daten sind als Teil des {agridat}-Pakets verfügbar:

dat <- as_tibble(agridat::john.alpha)
dat

# A tibble: 72 × 7
    plot rep   block gen   yield   row   col
   <int> <fct> <fct> <fct> <dbl> <int> <int>
 1     1 R1    B1    G11    4.12     1     1
 2     2 R1    B1    G04    4.45     2     1
 3     3 R1    B1    G05    5.88     3     1
 4     4 R1    B1    G22    4.58     4     1
 5     5 R1    B2    G21    4.65     5     1
 6     6 R1    B2    G10    4.17     6     1
 7     7 R1    B2    G20    4.01     7     1
 8     8 R1    B2    G02    4.34     8     1
 9     9 R1    B3    G23    4.23     9     1
10    10 R1    B3    G14    4.76    10     1
# ℹ 62 more rows

Der Datensatz enthält:

• rep: Drei vollständige Wiederholungen (R1, R2, R3)
• block: Sechs unvollständige Blöcke innerhalb jeder Wiederholung (B1-B6)
• gen: 24 Genotypen (G01-G24)
• yield: Ernteertrag in Tonnen pro Hektar
• row und col: Feldparzellenkoordinaten für die Visualisierung

Erkunden

Betrachten wir zunächst die deskriptiven Statistiken nach Genotyp:

dat %>% 
  group_by(gen) %>% 
  summarize(
    count = n(),
    mean_yield = mean(yield),
    sd_yield = sd(yield),
    min_yield = min(yield),
    max_yield = max(yield)
  ) %>%
  arrange(desc(mean_yield))

# A tibble: 24 × 6
   gen   count mean_yield sd_yield min_yield max_yield
   <fct> <int>      <dbl>    <dbl>     <dbl>     <dbl>
 1 G01       3       5.16    0.534      4.65      5.72
 2 G05       3       5.06    0.841      4.20      5.88
 3 G12       3       4.91    0.641      4.17      5.31
 4 G15       3       4.89    0.207      4.68      5.09
 5 G19       3       4.87    0.398      4.56      5.31
 6 G13       3       4.83    0.619      4.25      5.48
 7 G21       3       4.82    0.503      4.41      5.38
 8 G17       3       4.73    0.379      4.32      5.07
 9 G16       3       4.73    0.502      4.39      5.30
10 G06       3       4.71    0.464      4.25      5.18
# ℹ 14 more rows

Jeder Genotyp erscheint genau 3 mal (einmal pro Wiederholung). Genotyp G11 hat den höchsten mittleren Ertrag, während G24 den niedrigsten hat.

Untersuchen wir nun die Blockstruktur:

dat %>% 
  group_by(rep, block) %>% 
  summarize(
    count = n(),
    mean_yield = mean(yield),
    .groups = "drop"
  ) %>%
  arrange(rep, block)

# A tibble: 18 × 4
   rep   block count mean_yield
   <fct> <fct> <int>      <dbl>
 1 R1    B1        4       4.75
 2 R1    B2        4       4.29
 3 R1    B3        4       4.36
 4 R1    B4        4       4.33
 5 R1    B5        4       4.79
 6 R1    B6        4       4.58
 7 R2    B1        4       4.12
 8 R2    B2        4       4.23
 9 R2    B3        4       5.22
10 R2    B4        4       5.01
11 R2    B5        4       5.21
12 R2    B6        4       5.11
13 R3    B1        4       4.38
14 R3    B2        4       3.96
15 R3    B3        4       4.30
16 R3    B4        4       4.22
17 R3    B5        4       4.15
18 R3    B6        4       3.61

Wir können sehen, dass jeder der 18 unvollständigen Blöcke (6 Blöcke × 3 Wiederholungen) genau 4 Parzellen enthält. Visualisieren wir die Daten:

# Genotypen nach mittlerem Ertrag sortieren
gen_order <- dat %>% 
  group_by(gen) %>% 
  summarise(mean = mean(yield)) %>% 
  arrange(mean) %>% 
  pull(gen) %>% 
  as.character()

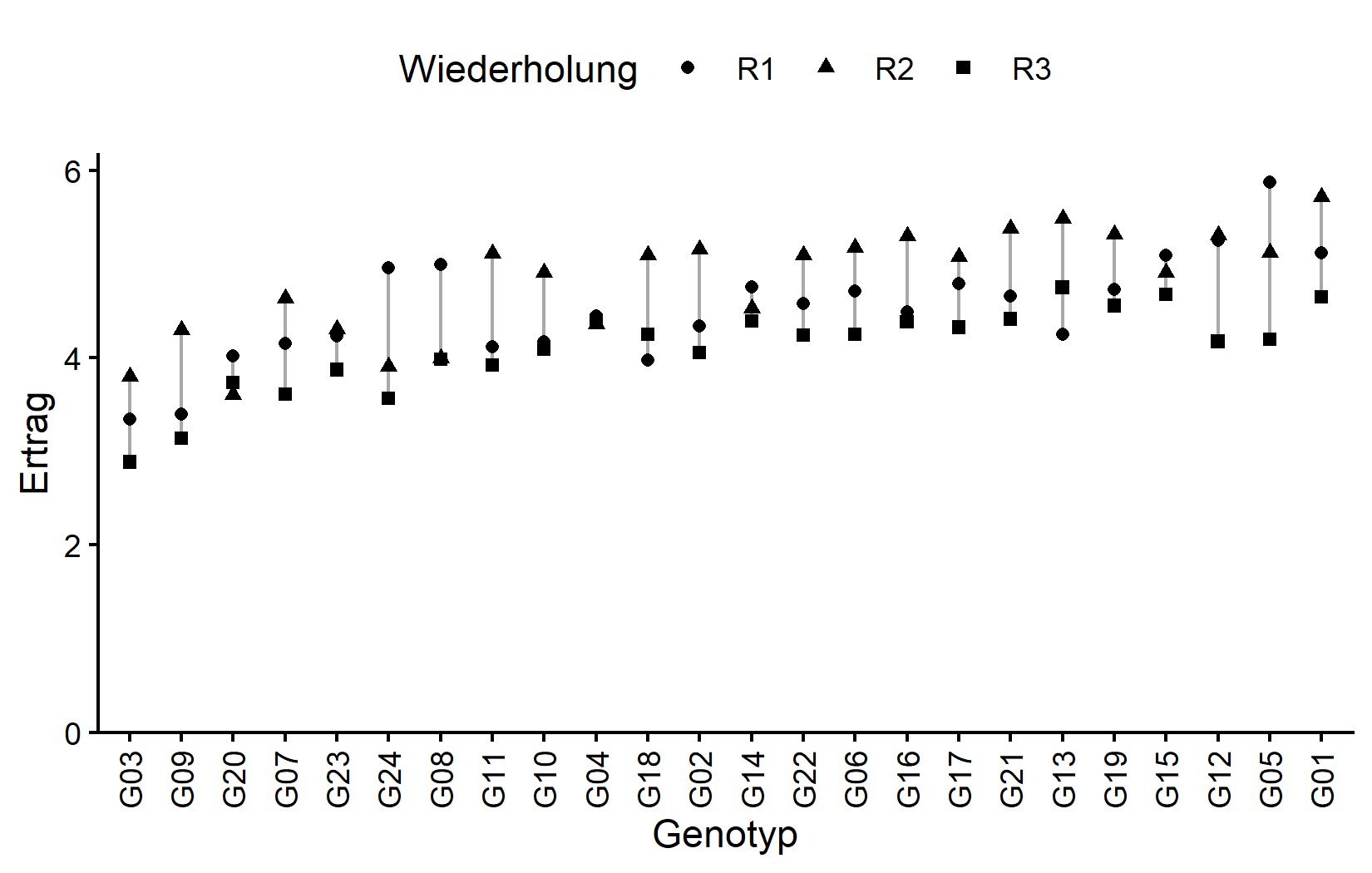
ggplot(data = dat) +
  aes(
    y = yield,
    x = gen,
    shape = rep
  ) +
  geom_line(
    aes(group = gen),
    color = "darkgrey"
  ) +
  geom_point() +
  scale_x_discrete(
    name = "Genotyp",
    limits = gen_order
  ) +
  scale_y_continuous(
    name = "Ertrag",
    limits = c(0, NA),
    expand = expansion(mult = c(0, 0.05))
  ) +
  scale_shape_discrete(
    name = "Wiederholung"
  ) +
  guides(shape = guide_legend(nrow = 1)) +
  theme_classic() +
  theme(
    legend.position = "top", 
    axis.text.x = element_text(angle = 90, vjust = 0.5)
  )

Die grauen Linien verbinden Beobachtungen desselben Genotyps über Wiederholungen hinweg und helfen, die Genotypkonsistenz zu visualisieren. Schauen wir uns nun das Feldlayout an:

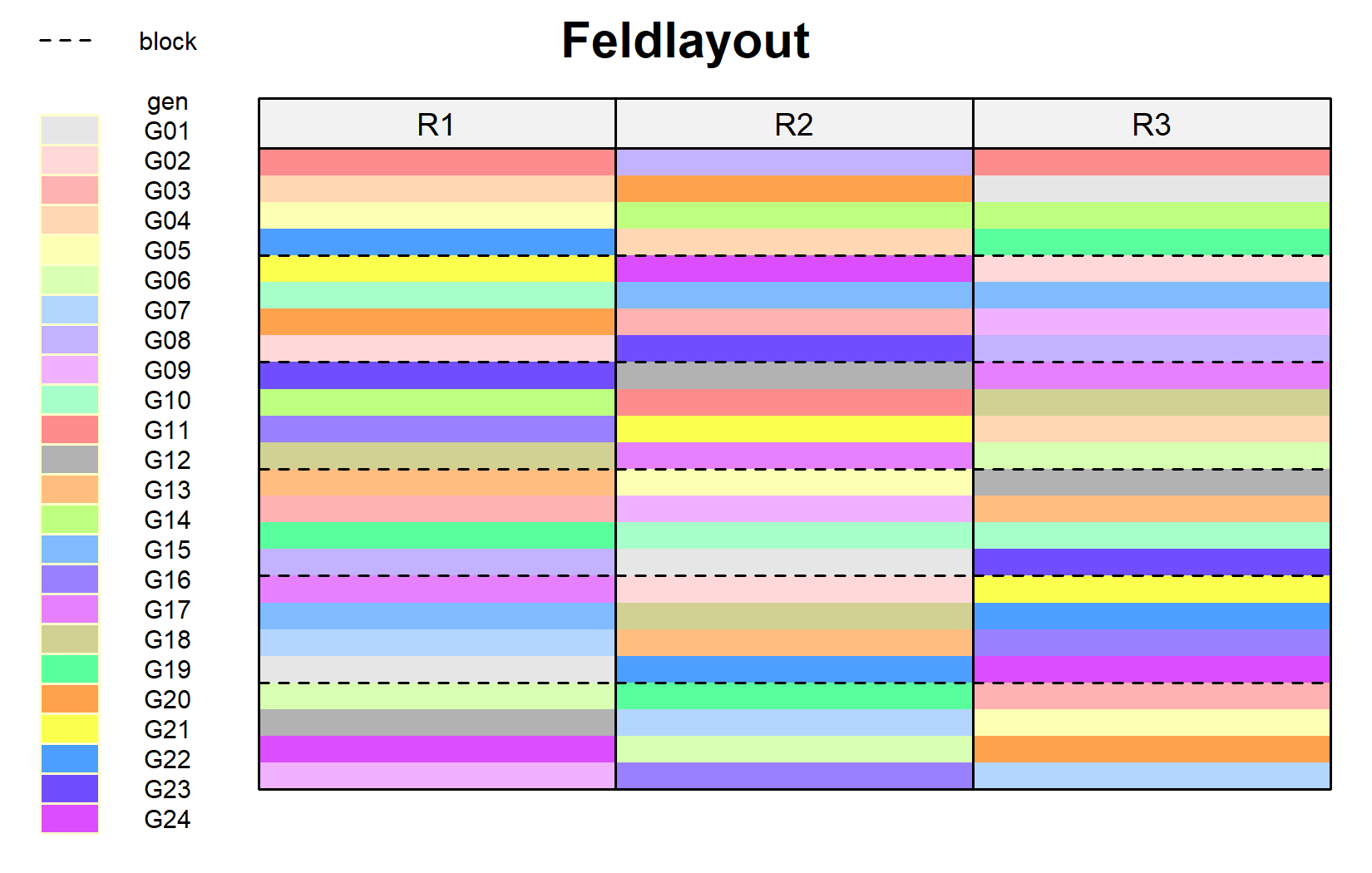
desplot(
  data = dat, 
  flip = TRUE,
  form = gen ~ col + row | rep, # Füllfarbe pro Genotyp, Panels pro Wiederholung
  out1 = block, # Linien zwischen unvollständigen Blöcken
  out1.gpar = list(col = "black", lwd = 1, lty = "dashed"),
  main = "Feldlayout",
  key.cex = 0.6,
  layout = c(3, 1) # alle Wiederholungen in einer Reihe erzwingen
)

Die gestrichelten Linien trennen die unvollständigen Blöcke innerhalb jeder Wiederholung. Beachten Sie, wie jeder Genotyp einmal pro Wiederholung erscheint, aber in verschiedenen Blöcken.

Modell und ANOVA

Modell mit zufaelligen unvollstaendigen Bloecken

Für ein Alpha-Design enthält das Modell:

• Feste Effekte: Genotyp (gen) und Wiederholung (rep)
• Zufällige Effekte: Unvollständige Blöcke genestelt innerhalb von Wiederholungen (rep:block)

Die unvollständigen Blöcke werden als zufällig behandelt, weil wir nicht an den spezifischen Blockeffekten selbst interessiert sind, sondern die Variation berücksichtigen wollen, die sie einführen. Dies ist der wesentliche Unterschied zu unseren vorherigen Analysen.

mod <- lmer(yield ~ gen + rep + (1 | rep:block),
            data = dat)

Die Syntax (1 | rep:block) spezifiziert, dass die Interaktion von rep und block (d.h. die 18 einzigartigen unvollständigen Blöcke) als zufälliger Effekt behandelt werden soll.

WarnungModellannahmen erfüllt?

An dieser Stelle (d.h. nach dem Modell-Fit und vor der ANOVA-Interpretation) sollte man prüfen, ob die Modellannahmen erfüllt sind. Mehr dazu im Anhang A1: Modelldiagnostik.

Durchführung der ANOVA

Für gemischte Modelle verwenden wir einen etwas anderen ANOVA-Ansatz mit Kenward-Roger-Freiheitsgraden, der genauere F-Tests für kleine Stichprobengrößen liefert:

ANOVA <- anova(mod, ddf = "Kenward-Roger")
ANOVA

Type III Analysis of Variance Table with Kenward-Roger's method
     Sum Sq Mean Sq NumDF  DenDF F value    Pr(>F)    
gen 10.5070 0.45683    23 35.498  5.3628 4.496e-06 ***
rep  1.5703 0.78513     2 11.519  9.2124  0.004078 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Die ANOVA zeigt, dass der Genotypeffekt statistisch signifikant ist (p < 0.05), was darauf hinweist, dass sich mindestens ein Genotyp von den anderen im Ertrag unterscheidet.

Mittelwertvergleiche

Wie in vorherigen Kapiteln verwenden wir emmeans(), um adjustierte Mittelwerte zu erhalten und Post-hoc-Vergleiche durchzuführen:

mean_comp <- mod %>% 
  emmeans(specs = ~ gen) %>%
  cld(adjust = "none", Letters = letters)

mean_comp

 gen emmean    SE   df lower.CL upper.CL .group    
 G03   3.50 0.199 44.3     3.10     3.90  a        
 G09   3.50 0.199 44.3     3.10     3.90  ab       
 G20   4.04 0.199 44.3     3.64     4.44   bc      
 G07   4.11 0.199 44.3     3.71     4.51    cd     
 G24   4.15 0.199 44.3     3.75     4.55    cd     
 G23   4.25 0.199 44.3     3.85     4.65    cde    
 G11   4.28 0.199 44.3     3.88     4.68    cde    
 G18   4.36 0.199 44.3     3.96     4.76    cdef   
 G10   4.37 0.199 44.3     3.97     4.77    cdef   
 G02   4.48 0.199 44.3     4.08     4.88    cdefg  
 G04   4.49 0.199 44.3     4.09     4.89    cdefg  
 G22   4.53 0.199 44.3     4.13     4.93    cdefgh 
 G08   4.53 0.199 44.3     4.13     4.93    cdefgh 
 G06   4.54 0.199 44.3     4.14     4.94    cdefgh 
 G17   4.60 0.199 44.3     4.20     5.00     defghi
 G16   4.73 0.199 44.3     4.33     5.13      efghi
 G12   4.76 0.199 44.3     4.35     5.16      efghi
 G13   4.76 0.199 44.3     4.36     5.16      efghi
 G14   4.78 0.199 44.3     4.37     5.18      efghi
 G21   4.80 0.199 44.3     4.39     5.20      efghi
 G19   4.84 0.199 44.3     4.44     5.24       fghi
 G15   4.97 0.199 44.3     4.57     5.37        ghi
 G05   5.04 0.199 44.3     4.64     5.44         hi
 G01   5.11 0.199 44.3     4.71     5.51          i

Results are averaged over the levels of: rep 
Degrees-of-freedom method: kenward-roger 
Confidence level used: 0.95 
significance level used: alpha = 0.05 
NOTE: If two or more means share the same grouping symbol,
      then we cannot show them to be different.
      But we also did not show them to be the same. 

Beachten Sie, dass diese Mittelwerte für sowohl Wiederholungs- als auch unvollständige Blockeffekte adjustiert sind. Die Kompaktbuchstabendarstellung zeigt, welche Genotypen sich signifikant voneinander unterscheiden, gemäß Fishers LSD-Test.

Visualisierung der Ergebnisse

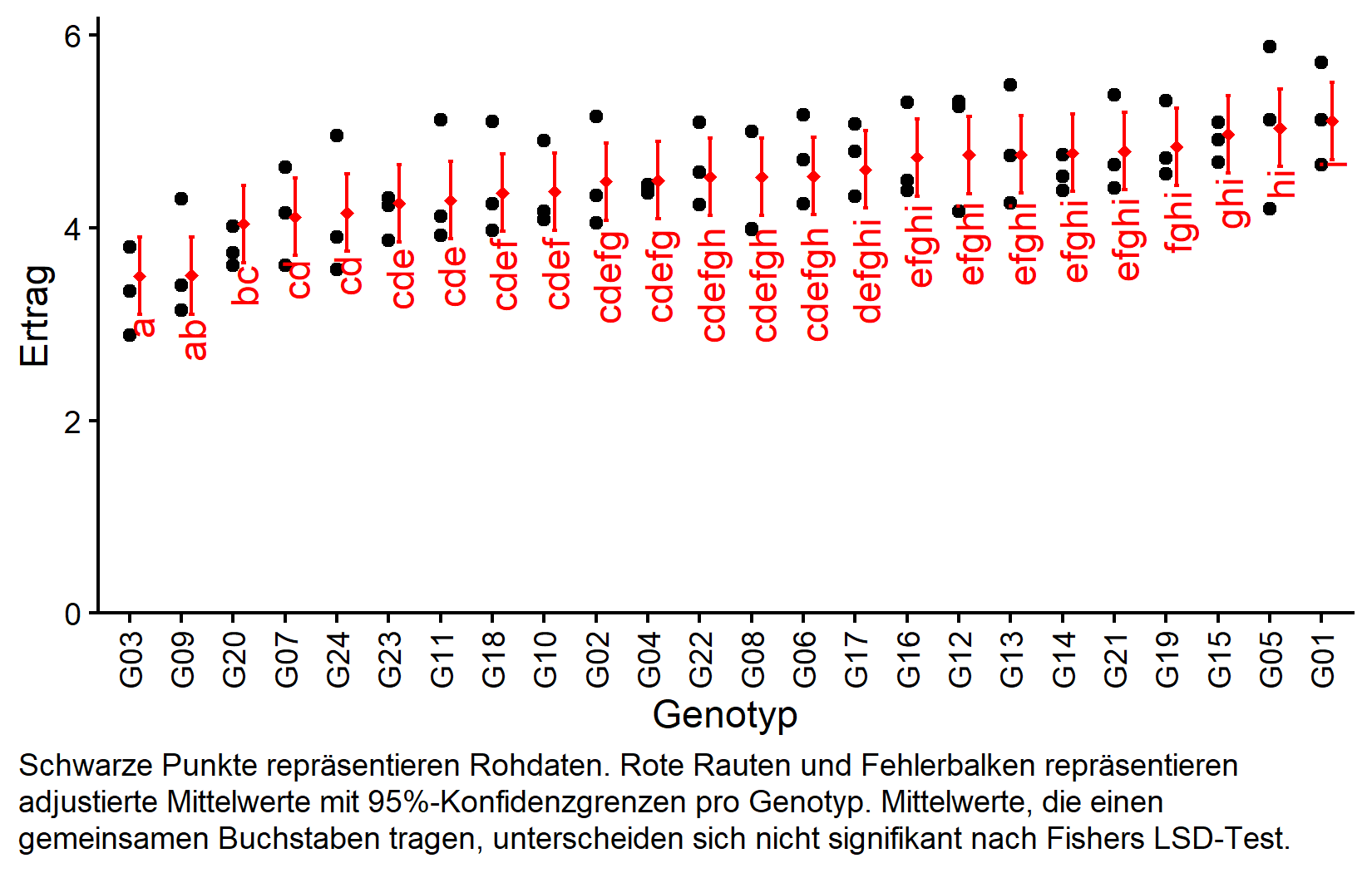
my_caption <- "Schwarze Punkte repräsentieren Rohdaten. Rote Rauten und Fehlerbalken repräsentieren adjustierte Mittelwerte mit 95%-Konfidenzgrenzen pro Genotyp. Mittelwerte, die einen gemeinsamen Buchstaben tragen, unterscheiden sich nicht signifikant nach Fishers LSD-Test."

ggplot() +
  aes(x = gen) +
  # schwarze Punkte für die Rohdaten
  geom_point(
    data = dat,
    aes(y = yield)
  ) +
  # rote Rauten für die adjustierten Mittelwerte
  geom_point(
    data = mean_comp,
    aes(y = emmean),
    shape = 18,
    color = "red",
    position = position_nudge(x = 0.2)
  ) +
  # rote Fehlerbalken für die Konfidenzgrenzen der adjustierten Mittelwerte
  geom_errorbar(
    data = mean_comp,
    aes(ymin = lower.CL, ymax = upper.CL),
    color = "red",
    width = 0.1,
    position = position_nudge(x = 0.2)
  ) +
  # rote Buchstaben 
  geom_text(
    data = mean_comp,
    aes(y = lower.CL, label = str_trim(.group)),
    color = "red",
    angle = 90,
    hjust = 1.1,
    position = position_nudge(x = 0.2)
  ) + 
  scale_x_discrete(
    name = "Genotyp",
    limits = as.character(mean_comp$gen)
  ) +
  scale_y_continuous(
    name = "Ertrag",
    limits = c(0, NA),
    expand = expansion(mult = c(0, 0.05))
  ) +
  labs(caption = my_caption) +
  theme_classic() +
  theme(plot.caption = element_textbox_simple(margin = margin(t = 5)),
        plot.caption.position = "plot",
        axis.text.x = element_text(angle = 90, vjust = 0.5))

Bonus: Designeffizienz

Die Effizienz eines unvollständigen Blockdesigns kann durch Vergleich mit dem analogen RCBD (unter Ignorierung der unvollständigen Blöcke) bewertet werden. Wir vergleichen die quadrierten Standardfehler der Differenzen:

# s.e.d. quadriert für Alpha-Design
avg_sed_alpha <- mod %>%
  emmeans(pairwise ~ "gen", adjust = "none", lmer.df = "kenward-roger") %>%
  pluck("contrasts") %>%
  as_tibble() %>%
  pull("SE") %>%
  mean()

# s.e.d. quadriert für RCBD (unter Ignorierung der unvollständigen Blöcke)
avg_sed_rcbd <- lm(yield ~ gen + rep, data = dat) %>% 
  emmeans(pairwise ~ "gen", adjust = "none") %>%
  pluck("contrasts") %>%
  as_tibble() %>%
  pull("SE") %>%
  mean()

# Effizienz
avg_sed_rcbd^2 / avg_sed_alpha^2

[1] 1.230428

Eine Effizienz > 1 zeigt an, dass das Alpha-Design effizienter ist als ein einfaches RCBD, was bedeutet, dass die unvollständigen Blöcke den Versuchsfehler erfolgreich reduziert haben.

Zusammenfassung

Sie haben nun gelernt, wie man Daten aus einem Alpha-Design analysiert, das das Blockbildungsprinzip auf Situationen erweitert, in denen vollständige Blöcke unpraktisch sind.

HinweisWichtige Erkenntnisse

1. Alpha-Designs sind auflösbare unvollständige Blockdesigns, die nützlich sind, wenn die Anzahl der Behandlungen zu groß für vollständige Blöcke ist.

2. Gemischte Modelle mit lmer() werden verwendet, um unvollständige Blockdesigns zu analysieren, wobei unvollständige Blöcke als zufällige Effekte behandelt werden.

3. Syntax für zufällige Effekte: Verwenden Sie (1 | factor) für zufällige Effekte anstelle von + factor für feste Effekte.

4. Das Modell enthält feste Genotyp- und Wiederholungseffekte plus zufällige unvollständige Blockeffekte: yield ~ gen + rep + (1 | rep:block).

5. Kenward-Roger-Freiheitsgrade liefern genauere F-Tests für gemischte Modelle mit kleinen Stichprobengrößen.

6. Die Designeffizienz kann durch Vergleich mit einem analogen RCBD bewertet werden - eine Effizienz > 1 bestätigt den Vorteil der unvollständigen Blockbildung.

Literatur

John, J. A., und E. R. Williams. 1995. „Cyclic and Computer Generated Designs“. Biometrical Journal 38 (7): 778–78. https://doi.org/10.1002/bimj.4710380703.