Um alle in diesem Kapitel verwendeten Pakete zu installieren und zu laden, führen Sie folgenden Code aus:
Zwei neue Aspekte
In diesem und dem nächsten Kapitel unterscheiden sich zwei Dinge fundamental von unseren bisherigen Kapiteln/Analysen:
Einerseits haben wir nun Daten aus einem geplanten Experiment, bei dem wir bewusst einen Behandlungsfaktor gewählt, das Experiment auf eine bestimmte Weise angeordnet und dann die Zielvariable gemessen haben. In unseren bisherigen Datensätzen haben wir mehr oder weniger eine spontane Bestandsaufnahme der Welt um uns herum gemacht.
Andererseits werden wir kategoriale Prädiktoren (Faktoren) anstelle von kontinuierlichen Prädiktoren analysieren. Somit ist unsere Zielvariable (\(y\)) nach wie vor kontinuierlich, aber unsere Prädiktorvariable (\(x\)) ist kategorial. Dementsprechend sind Korrelation und einfache lineare Regression nicht mehr geeignet. Stattdessen werden wir die Varianzanalyse (ANOVA) und Post-hoc-Tests (t-Test, Tukey-Test) zur Datenanalyse verwenden.
Der einzige Unterschied zwischen diesem und dem nächsten Kapitel liegt im verwendeten Versuchsdesign. In diesem Kapitel analysieren wir Daten aus einem vollständig randomisierten Versuchsdesign (CRD), dem einfachstmöglichen Design, während wir im nächsten Kapitel Daten aus einem randomisierten vollständigen Blockdesign (RCBD) analysieren werden. Dementsprechend werden wir uns in diesem Kapitel mehr auf den Wechsel zur Analyse kategorialer Prädiktoren konzentrieren, während das nächste Kapitel mehr auf das Versuchsdesign und die Unterschiede zwischen CRD und RCBD fokussiert.
Von der Regression zur ANOVA
Bisher haben wir Beziehungen zwischen kontinuierlichen Variablen mithilfe von Korrelation und Regression untersucht. Im Gegensatz dazu untersuchen wir in diesem Kapitel den Effekt kategorialer Prädiktoren (Faktoren) auf eine kontinuierliche Zielvariable. Beispielsweise könnten wir fragen: “Erzeugen verschiedene Pflanzensorten signifikant unterschiedliche Erträge?”
Dieser Wechsel von kontinuierlichen zu kategorialen Prädiktoren erfordert die Verwendung der Varianzanalyse (ANOVA) anstelle der einfachen linearen Regression, obwohl beide Techniken tatsächlich verwandt sind und auf demselben zugrunde liegenden Rahmen basieren: einem allgemeinen linearen Modell.
Daten
Für dieses Beispiel verwenden wir Daten aus einem Melonen-Sortenversuch. Vier verschiedene Melonensorten wurden getestet, wobei jede Sorte in sechs zufällig zugewiesenen Parzellen auf einem Feld angepflanzt wurde. Da die Zuweisung der Sorten zu den Parzellen vollkommen zufällig erfolgte, folgt dieses Experiment einem vollständig randomisierten Versuchsdesign (CRD).
Importieren wir die Daten:
Rows: 24 Columns: 4
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): variety
dbl (3): yield, row, col
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.# A tibble: 24 × 4
variety yield row col
<chr> <dbl> <dbl> <dbl>
1 v1 25.1 4 2
2 v1 17.2 1 6
3 v1 26.4 4 1
4 v1 16.1 1 4
5 v1 22.2 1 2
6 v1 15.9 2 4
7 v2 40.2 4 4
8 v2 35.2 3 1
9 v2 32.0 4 6
10 v2 36.5 2 1
# ℹ 14 more rowsDer Datensatz enthält Informationen über:
-
variety: Die Melonensorte (v1, v2, v3 und v4) -
yield: Die Ertragsmessung für jede Parzelle -
rowundcol: Die Reihen- und Spaltenkoordinaten jeder Parzelle im Feldlayout. Diese Informationen sind für die Analyse nicht notwendig, sondern nur erforderlich, wenn man einen Feldplan mitdesplot()darstellen möchte (siehe unten)
Formatierung
Ein wichtiger erster Schritt beim Arbeiten mit kategorialen Variablen ist sicherzustellen, dass sie ordnungsgemäß als Faktoren codiert sind. Standardmäßig hat R Spalten mit Text als Datentyp chr (character) importiert, aber es ist besser, sie sofort in fct (factor) für kategoriale Variablen zu konvertieren. Wir können diese Formatierung erreichen, indem wir die mutate()-Funktion aus dem dplyr-Paket verwenden und die ursprüngliche variety-Spalte mit sich selbst überschreiben, jedoch in einen Faktor konvertiert:
# A tibble: 24 × 4
variety yield row col
<fct> <dbl> <dbl> <dbl>
1 v1 25.1 4 2
2 v1 17.2 1 6
3 v1 26.4 4 1
4 v1 16.1 1 4
5 v1 22.2 1 2
6 v1 15.9 2 4
7 v2 40.2 4 4
8 v2 35.2 3 1
9 v2 32.0 4 6
10 v2 36.5 2 1
# ℹ 14 more rowsDieser Schritt ist vorteilhaft, weil Rs statistische Funktionen Faktoren möglicherweise anders behandeln als Zeichenvariablen. Mit Faktoren versteht R, dass wir es mit unterschiedlichen Stufen einer kategorialen Variablen zu tun haben.
Erkunden
Bevor wir mit der formalen Analyse beginnen, erkunden wir unsere Daten, um zu verstehen, womit wir arbeiten:
# A tibble: 4 × 6
variety count mean_yield sd_yield min_yield max_yield
<fct> <int> <dbl> <dbl> <dbl> <dbl>
1 v2 6 37.4 3.95 32.0 43.3
2 v4 6 29.9 2.23 27.6 33.2
3 v1 6 20.5 4.69 15.9 26.4
4 v3 6 19.5 5.56 11.4 25.9Offensichtlich hat Sorte v2 den höchsten mittleren Ertrag, gefolgt von v4, v1 und v3. Sogar der niedrigste Wert von v2 ist höher als alle Werte von v1 und v3. Visualisieren wir auch die Daten:
myplot <- ggplot(data = dat) +
aes(y = yield, x = variety) +
geom_point() +
scale_x_discrete(
name = "Sorte"
) +
scale_y_continuous(
name = "Ertrag",
limits = c(0, NA),
expand = expansion(mult = c(0, 0.1))
) +
theme_classic()
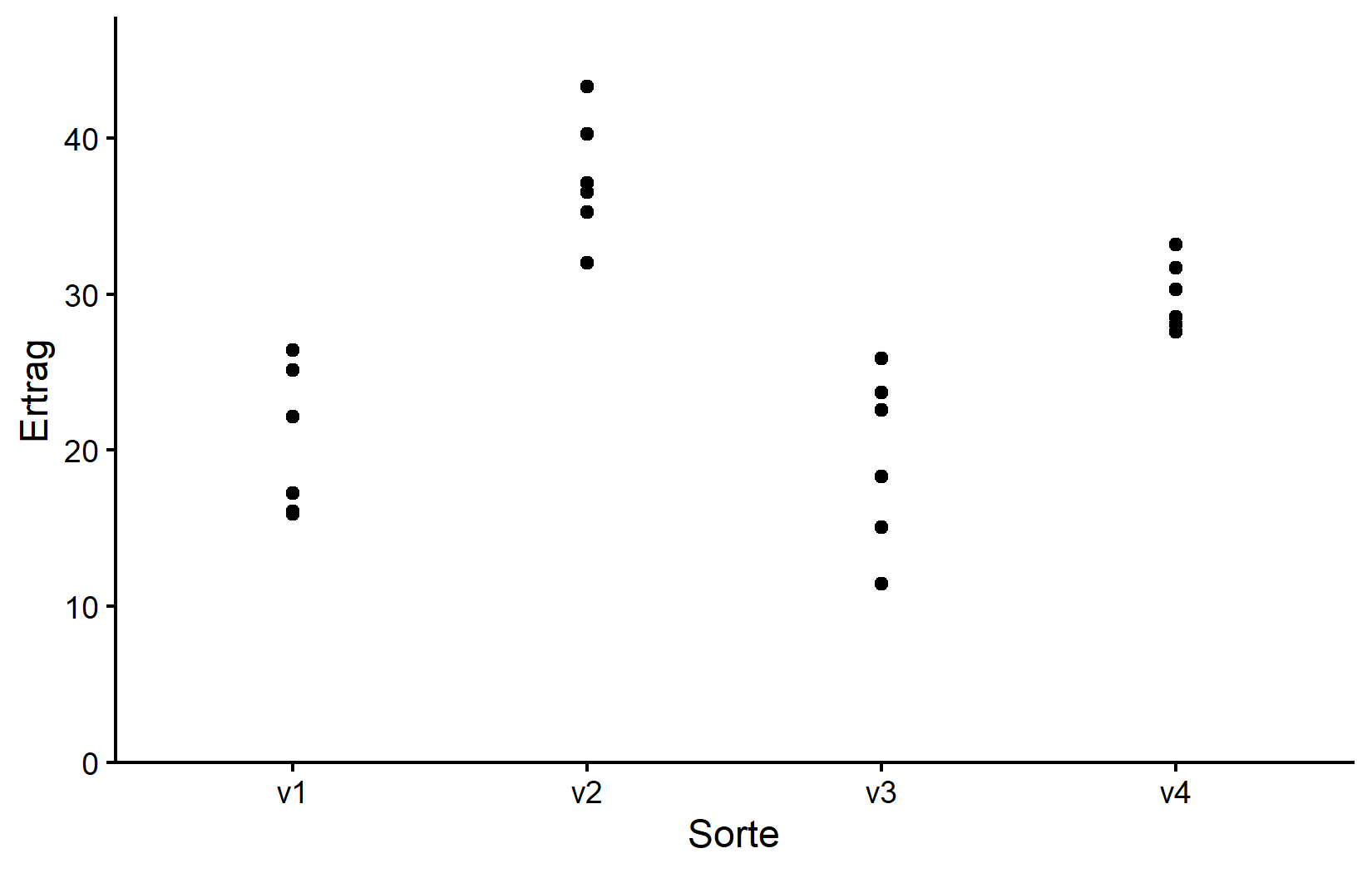
myplotBeachten Sie, dass wir, obwohl wir nun eine kategoriale x-Variable haben, größtenteils denselben ggplot-Code wie zuvor verwendet haben. Der einzige Unterschied ist, dass wir nun scale_x_discrete() anstelle von scale_x_continuous() verwenden müssen, um die x-Achse anzupassen. Die y-Achse ist nach wie vor kontinuierlich, sodass wir weiterhin scale_y_continuous() verwenden können.
Entsprechend ist die resultierende Darstellung immer noch ein Streudiagramm mit einem Punkt pro Beobachtung. Da wir jedoch eine kategoriale x-Variable haben, sind die Punkte nun nach Sorte gruppiert. Außerdem kann es zwischen den Sorten niemals Punkte geben, und daher wäre es auch unsinnig, beispielsweise eine Regressionslinie an die Daten anzupassen.
Je nach Ihrem Hintergrund und Ihren Betreuern sind Sie möglicherweise daran gewöhnt, Boxplots anstelle von Streudiagrammen zu sehen. Boxplots sind eine großartige Möglichkeit, die Verteilung der Daten innerhalb jeder Kategorie zu visualisieren. Verwenden wir jedoch tatsächlich nicht Boxplots anstelle von Streudiagrammen, sondern zusätzlich zu Streudiagrammen. Auf diese Weise können wir die einzelnen Datenpunkte und die Verteilung der Daten gleichzeitig sehen. Das ist durchaus erlaubt und ich empfehle es sehr. Da wir unser ggplot von oben in myplot gespeichert haben, können wir einfach eine weitere Schicht zu dieser Darstellung hinzufügen:
myplot +
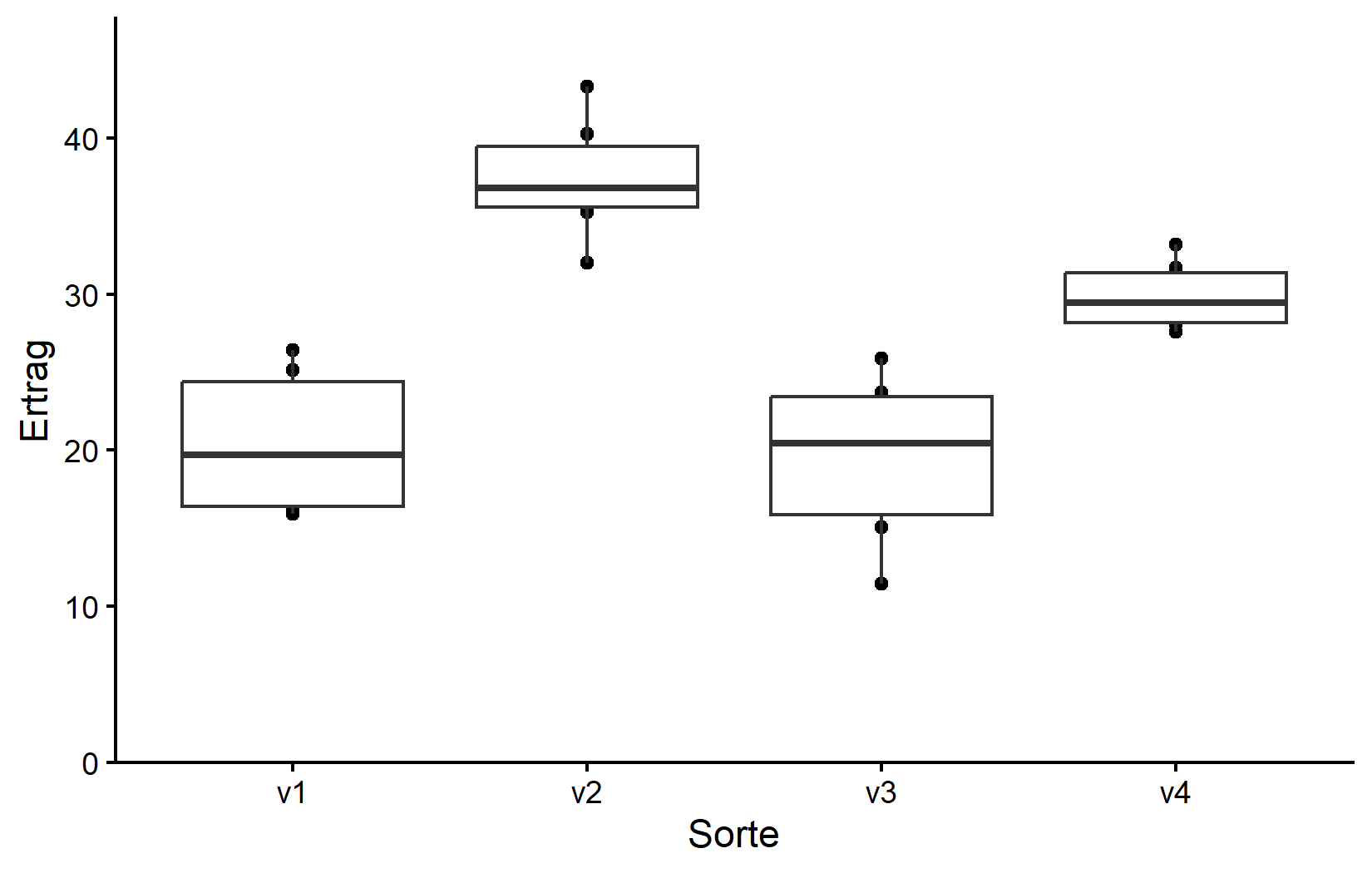
geom_boxplot()Da wir jedoch geom_boxplot() nach geom_point() hinzugefügt haben (und weil es dieselbe aes() verwendet), werden die Boxen direkt über den Punkten gezeichnet und verdecken daher einige von ihnen. Wir können stattdessen die Boxen dünner machen und zur Seite verschieben für eine noch bessere Darstellung:
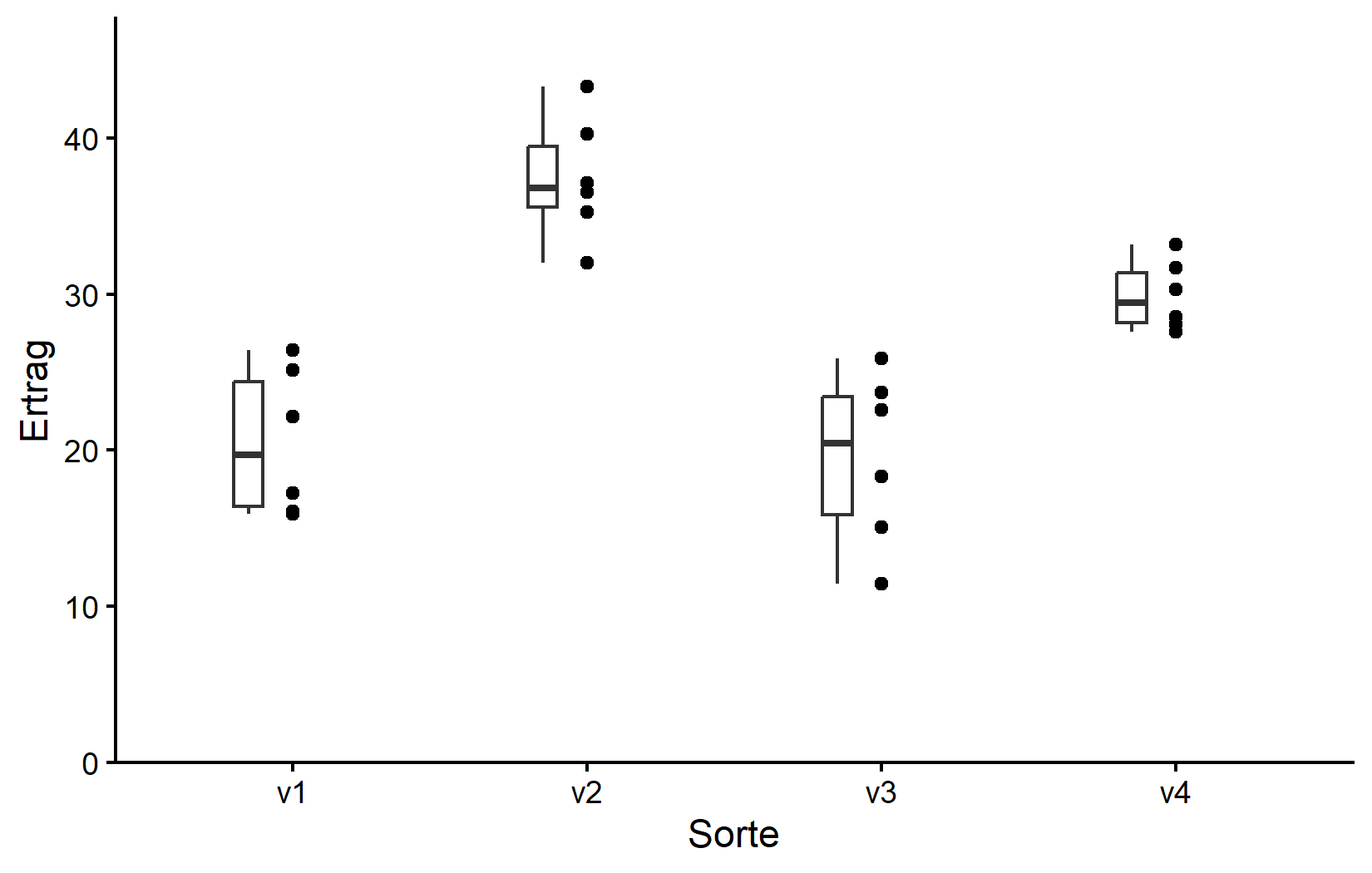
myplot +
geom_boxplot(
width = 0.1, # 10% Breite
position = position_nudge(x = -0.15) # nach links verschieben
)Wie oft der Fall, gibt uns diese Darstellung ein besseres Gefühl für die Daten als nur Tabellen, obwohl beispielsweise die vier Mittelwerte hier nicht einmal gezeigt werden.
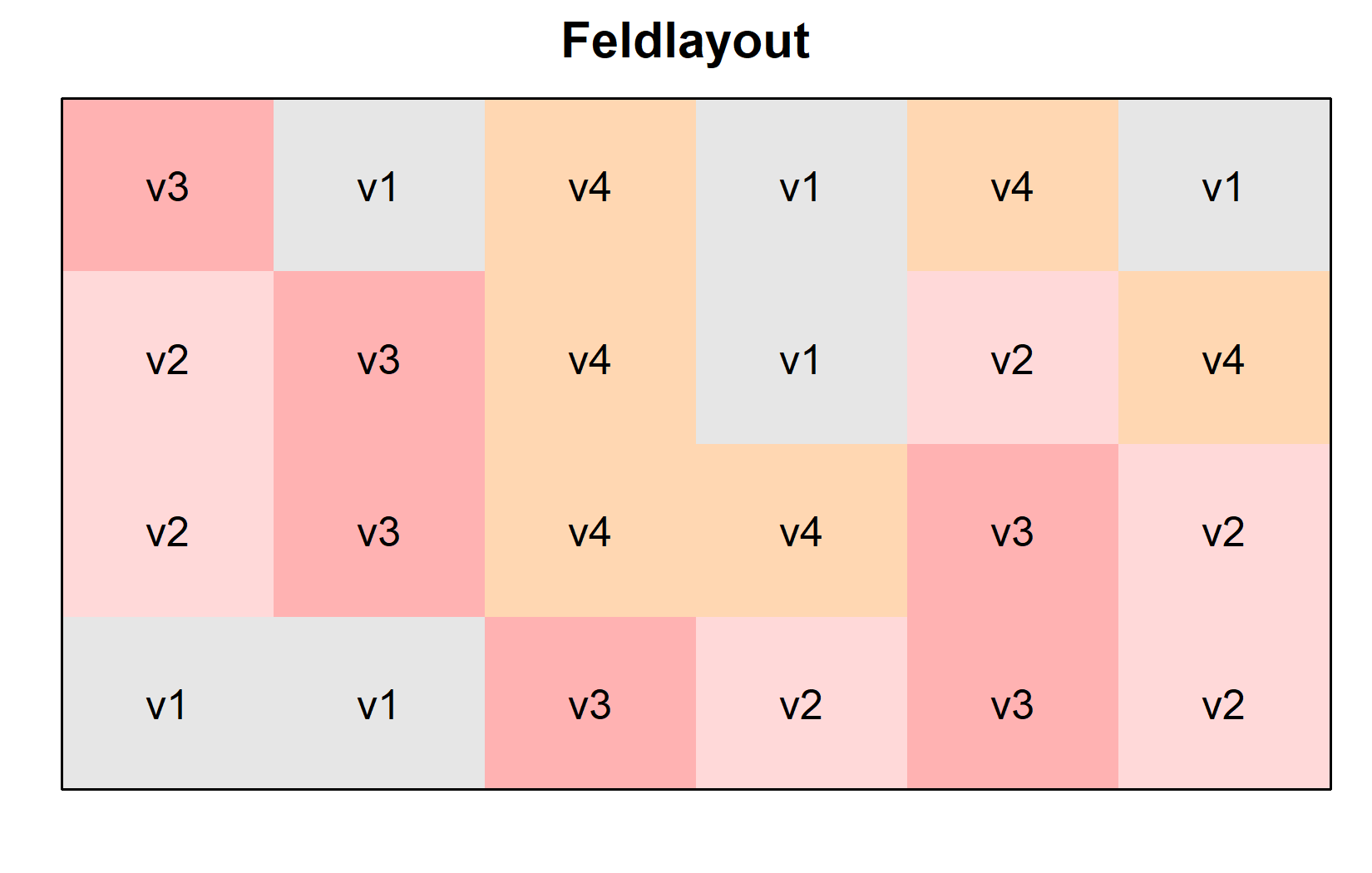
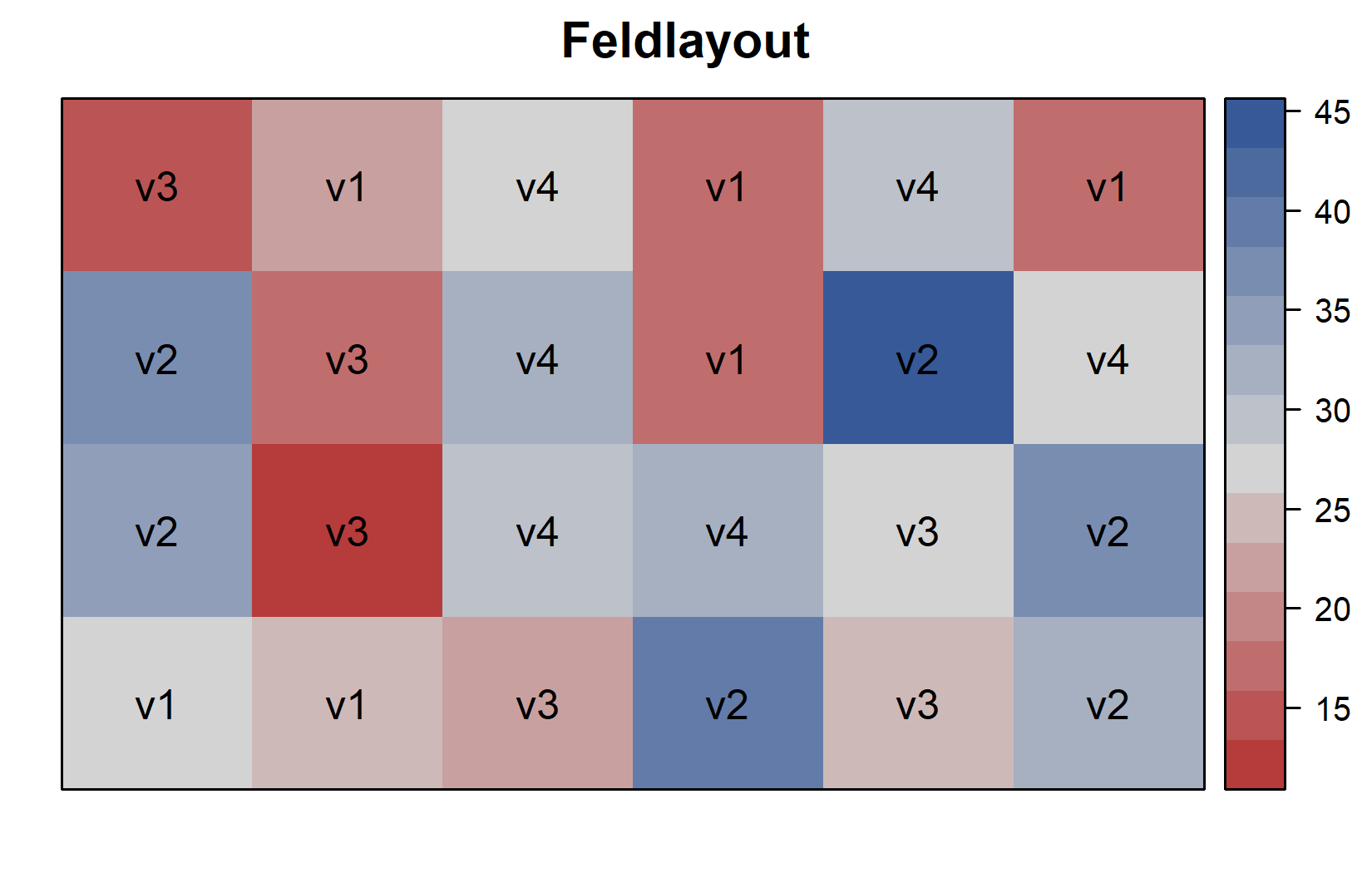
Da dies außerdem ein Feldversuch mit einem spezifischen Layout ist, visualisieren wir den Feldplan, um zu verstehen, wie die Sorten räumlich verteilt waren. Dies kann sehr schön gemacht werden, solange man die Koordinaten jeder Versuchseinheit (d.h. Feldparzelle) auf dem Feld hat, wie wir sie in den Spalten row und col haben. Man kann dann die desplot()-Funktion aus dem {desplot}-Paket verwenden:
desplot(
data = dat,
flip = TRUE, # Reihe 1 oben, nicht unten
form = variety ~ col + row, # Füllfarbe pro Sorte; Spalten-/Reiheninformation
text = variety, # Sortennamen pro Parzelle
cex = 1, # Sortennamen: Schriftgröße
main = "Feldlayout", # Diagrammtitel
show.key = FALSE # Legende ausblenden
)Diese Darstellung bestätigt, dass die Sorten zufällig über das Feld verteilt wurden, was charakteristisch für ein vollständig randomisiertes Versuchsdesign (CRD) ist. Wir können eine zweite Version dieses Feldplans erstellen, in der wir die Parzellen nach ihrem Ertrag anstatt nach ihrer Sorte einfärben. Dies kann durch einfaches Ändern des form-Arguments in der desplot()-Funktion erreicht werden:
desplot(
data = dat,
flip = TRUE, # Reihe 1 oben, nicht unten
form = yield ~ col + row, # Füllfarbe pro Sorte; Spalten-/Reiheninformation
text = variety, # Sortennamen pro Parzelle
cex = 1, # Sortennamen: Schriftgröße
main = "Feldlayout", # Diagrammtitel
show.key = FALSE # Legende ausblenden
)Wir haben nun genug deskriptive Statistiken und Visualisierungen erstellt. Der nächste Schritt ist die Datenanalyse und der Test, ob die Ertragsunterschiede zwischen den Sorten statistisch signifikant sind. Hier kommt die Varianzanalyse (ANOVA) ins Spiel.
Modell und ANOVA
Verstehen der einfaktoriellen ANOVA
Die Varianzanalyse (ANOVA) ist eine statistische Methode, die verwendet wird, um Unterschiede zwischen Gruppenmittelwerten zu testen. In unserem Fall möchten wir bestimmen, ob es signifikante Ertragsunterschiede zwischen den vier Melonensorten gibt.
Die einfaktorielle ANOVA behandelt die Frage: “Gibt es einen signifikanten Unterschied zwischen den Gruppenmittelwerten?” Sie wird “einfaktoriell” genannt, weil sie nur einen kategorialen Prädiktor (die Sorte) umfasst. Die Nullhypothese ist, dass alle Gruppenmittelwerte gleich sind:
\(H_0: \mu_A = \mu_B = \mu_C = \mu_D\)
Die Alternativhypothese ist, dass sich mindestens ein Gruppenmittelwert von den anderen unterscheidet. Beachten Sie, dass wir den griechischen Buchstaben \(\mu\) verwenden, um den wahren Mittelwert jeder Sorte zu bezeichnen. In diesem Fall haben wir vier Sorten (A, B, C und D), also haben wir vier Mittelwerte. Die Schätzungen für diese Mittelwerte basierend auf unseren Stichproben-/Versuchsdaten werden stattdessen mit \(\bar{y}_A\), \(\bar{y}_B\), \(\bar{y}_C\) und \(\bar{y}_D\) bezeichnet. Dies ist analog dazu, wie wir den griechischen Buchstaben \(\rho\) verwendet haben, um den wahren/Populations-Korrelationskoeffizienten zu bezeichnen, aber den Buchstaben \(r\) für den Stichproben-Korrelationskoeffizienten verwendet haben.
Unter der Haube funktioniert ANOVA durch den Vergleich von:
- Die Variation zwischen Gruppen (wie unterschiedlich die Gruppenmittelwerte voneinander sind)
- Die Variation innerhalb Gruppen (wie viel Streuung/Rauschen innerhalb jeder Gruppe existiert)
Wenn die Variation zwischen den Gruppen viel größer ist als die Variation innerhalb der Gruppen, haben wir Evidenz dafür, dass sich die Gruppenmittelwerte signifikant unterscheiden.
Anpassung des Modells
In R passen wir ein lineares Modell mit der lm()-Funktion an, genau wie wir es bei der Regression getan haben. Der wesentliche Unterschied ist, dass unser Prädiktor \(x\) nun ein kategorialer Faktor und keine kontinuierliche Variable ist. R weiß dies, wegen der Formatierung der variety-Spalte - als Faktor. Obwohl wir also im Grunde dieselbe Formel wie zuvor schreiben (y ~ x), ist die Interpretation anders. Dies sieht man sofort beim Betrachten der Ergebnisse:
mod <- lm(yield ~ variety, data = dat)
mod
Call:
lm(formula = yield ~ variety, data = dat)
Coefficients:
(Intercept) varietyv2 varietyv3 varietyv4
20.4900 16.9133 -0.9983 9.4067 Sicher, es gibt wieder einen Achsenabschnitt, aber dann gibt es nicht eine Steigung, sondern stattdessen drei weitere Koeffizienten für die Sorten v2, v3 und v4. Offensichtlich können wir hier keine Steigung haben, da wir keine Zahl mit dem Namen einer Sorte multiplizieren können. Stattdessen erhält jede Sorte ihren eigenen zusätzlichen Achsenabschnitt. Nun, jede Sorte außer einer - v1 scheint zu fehlen. Sie fehlt nicht wirklich. Stattdessen wird v1 auf 0 gesetzt und ist somit die Referenzstufe, mit der alle anderen Sorten verglichen werden.
Beachten Sie, dass wir uns bei faktoriellen Experimenten typischerweise auf die ANOVA-Tabelle anstatt auf diese Koeffizienten konzentrieren. Siehe jedoch die Videoerklärung für eine detailliertere Diskussion der Koeffizienten und ihrer Interpretation.
An dieser Stelle (d.h. nach dem Modell-Fit und vor der ANOVA-Interpretation) sollte man prüfen, ob die Modellannahmen erfüllt sind. Mehr dazu im Anhang A1: Modelldiagnostik.
Durchführung der ANOVA
Wir können aus unserem Modell eine ANOVA-Tabelle mit der anova()-Funktion erstellen:
ANOVA <- anova(mod)
ANOVAAnalysis of Variance Table
Response: yield
Df Sum Sq Mean Sq F value Pr(>F)
variety 3 1291.48 430.49 23.418 9.439e-07 ***
Residuals 20 367.65 18.38
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die ANOVA-Tabelle liefert:
- Df: Freiheitsgrade für den Faktor (Sorten) und Residuen
- Sum Sq: Quadratsummen, die die Variation messen
- Mean Sq: Mittlere Quadratsummen (Sum Sq / Df)
- F value: F-Statistik (Verhältnis der Variation zwischen Gruppen zur Variation innerhalb der Gruppen)
- Pr(>F): p-Wert für den F-Test
Wie bereits gesagt, vergleicht diese Tabelle die Variation zwischen Gruppen (Sorten) mit der Variation innerhalb der Gruppen (Residuen). Wenn die F-Statistik groß und der p-Wert klein ist, verwerfen wir die Nullhypothese und schließen, dass sich mindestens ein Gruppenmittelwert signifikant von den anderen unterscheidet. Wir werden jedoch nicht ins Detail gehen, wie diese einzelnen Werte berechnet werden, aber graben Sie gerne tiefer, beispielsweise über die nachstehenden Quellen.
Der p-Wert ist sehr klein und < 0,05, was uns dazu führt, die Nullhypothese zu verwerfen und somit darauf hinweist, dass es statistisch signifikante Ertragsunterschiede zwischen den Sorten gibt. Die ANOVA sagt uns jedoch nur, dass es Unterschiede gibt, nicht welche spezifischen Sorten sich voneinander unterscheiden. Dafür können wir die Mittelwerte über Post-hoc-Tests vergleichen.
Mittelwertvergleiche
Verstehen von Post-hoc-Tests
Sobald wir durch die ANOVA festgestellt haben, dass es signifikante Unterschiede zwischen den Gruppen gibt, möchten wir typischerweise wissen, welche spezifischen Gruppen sich voneinander unterscheiden. Hier kommen Post-hoc-Tests ins Spiel.
Gängige Post-hoc-Tests umfassen Fishers LSD-Test, Tukeys HSD-Test und die Bonferroni-Holm-Korrektur. Fishers LSD ist im Wesentlichen ein Standard-t-Test, verwendet jedoch die gepoolte Standardabweichung aus der Modellresidualvarianz für alle Vergleiche.
Allen ist gemeinsam, dass ein Test für jedes Gruppenpaar durchgeführt wird. Wenn wir beispielsweise drei Gruppen (A, B & C) haben, würden wir drei Tests durchführen (A vs B, B vs C und A vs C). Post-hoc-Tests werden “post hoc” (“nach diesem”) genannt, weil sie nach der anfänglichen Analyse durchgeführt werden, die angezeigt hat, dass Unterschiede existieren, und es Forschern ermöglichen zu bestimmen, wo genau diese Unterschiede zwischen mehreren Gruppen liegen.
Für den Moment reicht es zu verstehen, dass diese Tests verwendet werden, um zu bestimmen, ob sich spezifische Gruppenmittelwerte signifikant voneinander unterscheiden, aber graben Sie gerne tiefer, beispielsweise über die nachstehenden Quellen.
Verwendung des emmeans-Pakets
Wir werden tatsächlich nicht Funktionen wie t.test() verwenden, die die Rohdaten als Input verwenden würden, um einen einzelnen t-Test zu berechnen. Stattdessen werden wir die emmeans()-Funktion aus dem emmeans-Paket verwenden, die automatisch geschätzte Randmittelwerte (EMMs; auch bekannt als kleinste-Quadrate-Mittelwerte oder adjustierte Mittelwerte) für jede Gruppe berechnet, unter Berücksichtigung der Modellstruktur und Residualvarianz:
# Adjustierte Mittelwerte für jede Sorte berechnen
means <- emmeans(mod, specs = ~ variety)
means variety emmean SE df lower.CL upper.CL
v1 20.5 1.75 20 16.8 24.1
v2 37.4 1.75 20 33.8 41.1
v3 19.5 1.75 20 15.8 23.1
v4 29.9 1.75 20 26.2 33.5
Confidence level used: 0.95 Dies sind die geschätzten mittleren Erträge für jede Sorte, adjustiert für das Modell. Bei einem einfachen einfaktoriellen Design wie unserem entsprechen diese den arithmetischen Mittelwerten, aber bei komplexeren Designs können sie sich unterscheiden. Mit anderen Worten: Da unser Modell so sehr einfach ist, wurden diese adjustierten Mittelwerte tatsächlich gar nicht adjustiert und sind identisch mit den Sortenmittelwerten, die wir oben berechnet haben. In komplexeren Modellen und mit unausgewogenen Daten ist das jedoch möglicherweise nicht der Fall. In jedem Fall ist ein weiterer Vorteil der Verwendung von emmeans(), dass es automatisch jeden Mittelwert mit jedem anderen Mittelwert vergleicht:
# Paarweise Vergleiche
pairs <- pairs(means, adjust = "tukey")
pairs contrast estimate SE df t.ratio p.value
v1 - v2 -16.913 2.48 20 -6.833 <0.0001
v1 - v3 0.998 2.48 20 0.403 0.9772
v1 - v4 -9.407 2.48 20 -3.800 0.0057
v2 - v3 17.912 2.48 20 7.236 <0.0001
v2 - v4 7.507 2.48 20 3.033 0.0307
v3 - v4 -10.405 2.48 20 -4.203 0.0023
P value adjustment: tukey method for comparing a family of 4 estimates Diese Ausgabe zeigt alle paarweisen Vergleiche zwischen Sorten. Zum Beispiel: Der Vergleich zwischen v1 und v2 zeigt einen Unterschied von -16.913. Sie können dies leicht überprüfen, indem Sie die obige Mittelwerttabelle betrachten. Der Mittelwert für v1 ist 20,5 und für v2 ist 37,4, also ist v1 - v2 tatsächlich -16,9. Neben diesem absoluten Unterschied zeigt die Tabelle jedoch auch den Standardfehler, die Freiheitsgrade, das t-Verhältnis und den p-Wert, die zu diesem Unterschied gehören. Da wir adjust = "tukey" geschrieben haben, entspricht jeder p-Wert einem Tukey-Test (verwenden Sie adjust = "none" für Fishers LSD-Test). Dementsprechend liegen alle p-Werte außer einem unter 0,05, was darauf hinweist, dass sich alle Sorten signifikant voneinander unterscheiden, außer v1 - v3.
Kompakte Buchstabendarstellung
Es ist wahrscheinlich, dass das Ausführen des nachstehenden Codes zum ersten Mal einen FEHLER verursacht. Dies liegt wahrscheinlich an einem seltsamen Bug mit der cld()-Funktion. Er kann normalerweise behoben werden, indem R neu gestartet und der Code erneut ausgeführt wird. Mit anderen Worten: Der FEHLER erscheint nur beim allerersten Mal, wenn Sie cld() ausführen. Wenn Sie es erneut ausführen, sollte es funktionieren. Wenn Sie also diesen FEHLER sehen, schließen und öffnen Sie entweder RStudio vollständig oder klicken Sie Session > Restart R in der Menüleiste. Denken Sie daran, dass Sie danach den gesamten Code ab dem Laden der Pakete und dem Importieren der Daten erneut ausführen müssen.
Eine gängige Methode, solche Mittelwertvergleichsergebnisse zu präsentieren, ist eine “kompakte Buchstabendarstellung” (CLD), bei der Mittelwerte, die sich nicht signifikant unterscheiden, denselben Buchstaben teilen:
# Kompakte Buchstabendarstellung
mean_comp <- cld(means, Letters = letters, adjust = "tukey")
mean_comp variety emmean SE df lower.CL upper.CL .group
v3 19.5 1.75 20 14.7 24.3 a
v1 20.5 1.75 20 15.7 25.3 a
v4 29.9 1.75 20 25.1 34.7 b
v2 37.4 1.75 20 32.6 42.2 c
Confidence level used: 0.95
Conf-level adjustment: sidak method for 4 estimates
P value adjustment: tukey method for comparing a family of 4 estimates
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Sorten, die denselben Buchstaben in der .group-Spalte teilen, unterscheiden sich nicht signifikant voneinander. Zum Beispiel sind Sorten, die beide den Buchstaben “a” haben, nicht signifikant voneinander verschieden. Diese Darstellung ist also kompakt, weil sie die allgemeinen Befunde all unserer sechs Tukey-Tests (statistisch signifikant oder nicht) über eine kurze Kombination von Buchstaben neben unseren vier Mittelwerten anzeigt.
Falls Sie sich wegen der Notiz wundern, die wir beim Ausführen des Codes erhalten haben Note: adjust = "tukey" was changed to "sidak" because "tukey" is only appropriate for one set of pairwise comparison, besuchen Sie bitte das Kapitel “kompakte Buchstabendarstellung” (CLD). Dort finden Sie auch andere Informationen zu all dem, die über diese Einführung hinausgehen.
Kombination der Schritte
Beachten Sie, dass wir diese Ergebnisse zwar gerade in mehreren Schritten erhalten haben, dies jedoch nur getan wurde, um das Verständnis zu erleichtern. In der Praxis können wir all dies in einem Befehl kombinieren:
mean_comp variety emmean SE df lower.CL upper.CL .group
v3 19.5 1.75 20 14.7 24.3 a
v1 20.5 1.75 20 15.7 25.3 a
v4 29.9 1.75 20 25.1 34.7 b
v2 37.4 1.75 20 32.6 42.2 c
Confidence level used: 0.95
Conf-level adjustment: sidak method for 4 estimates
P value adjustment: tukey method for comparing a family of 4 estimates
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Visualisierung der Ergebnisse
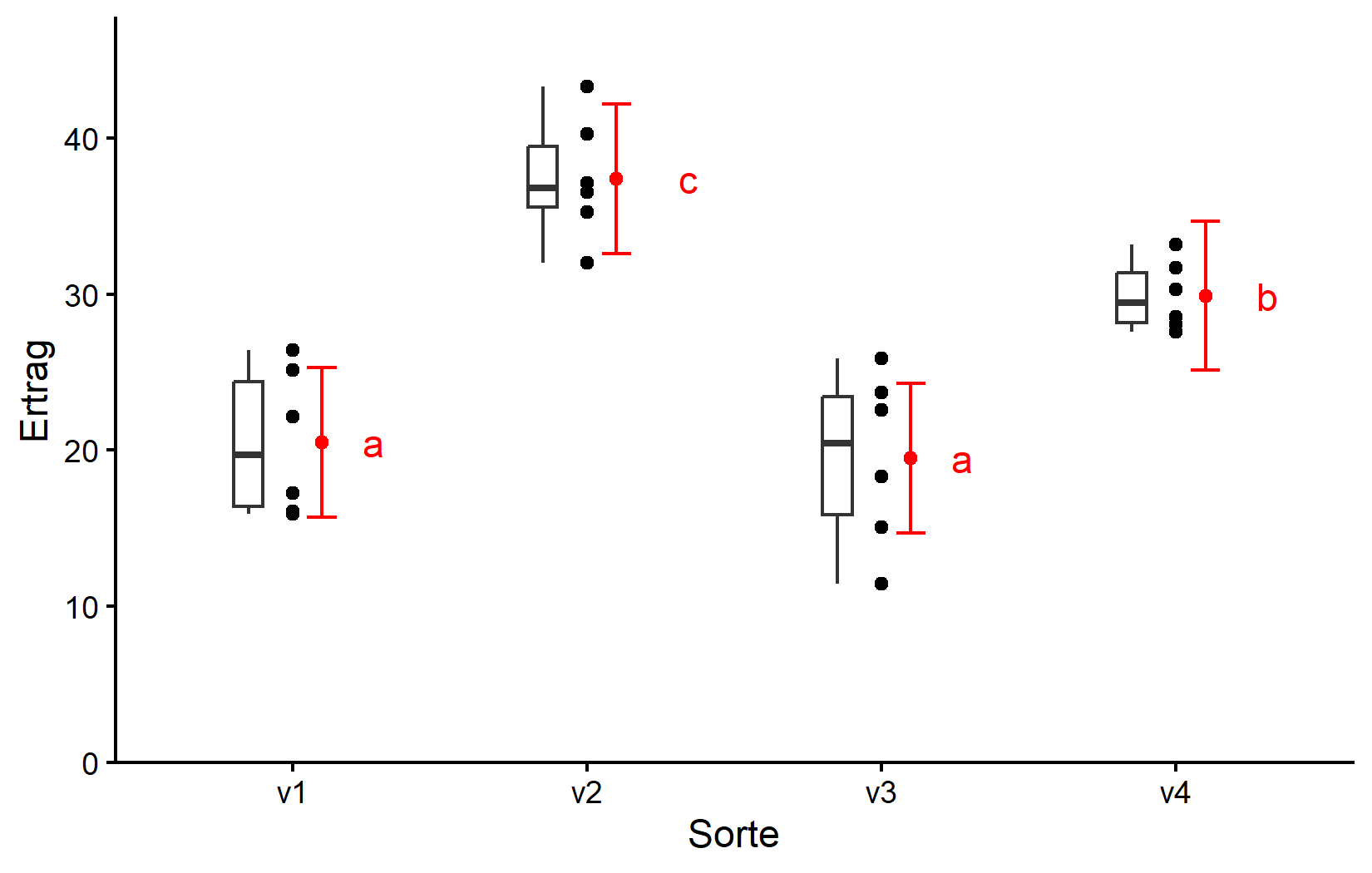
Erstellen wir schließlich eine Darstellung, die die Rohdaten mit unseren statistischen Ergebnissen kombiniert.
ggplot() +
aes(x = variety) +
# schwarze Punkte repräsentieren die Rohdaten
geom_point(
data = dat,
aes(y = yield)
) +
# schwarze Boxen repräsentieren die Verteilung der Rohdaten
geom_boxplot(
data = dat,
aes(y = yield),
width = 0.1, # 10% Breite
position = position_nudge(x = -0.15) # nach links verschieben
) +
# rote Punkte repräsentieren die adjustierten Mittelwerte
geom_point(
data = mean_comp,
aes(y = emmean),
color = "red",
position = position_nudge(x = 0.1)
) +
# rote Fehlerbalken repräsentieren die Konfidenzgrenzen der adjustierten Mittelwerte
geom_errorbar(
data = mean_comp,
aes(ymin = lower.CL, ymax = upper.CL),
color = "red",
width = 0.1,
position = position_nudge(x = 0.1)
) +
# rote Buchstaben
geom_text(
data = mean_comp,
aes(y = emmean, label = .group),
color = "red",
position = position_nudge(x = 0.2),
hjust = 0
) +
scale_x_discrete(
name = "Sorte"
) +
scale_y_continuous(
name = "Ertrag",
limits = c(0, NA),
expand = expansion(mult = c(0, 0.1))
) +
theme_classic()Wir werden im nächsten Kapitel mehr darüber sprechen, wie man diesen ggplot erstellt. Seien Sie sich vorerst bewusst, dass
- schwarze Punkte Rohdaten repräsentieren,
- schwarze Boxen die Verteilung der Rohdaten repräsentieren,
- rote Punkte und Fehlerbalken adjustierte Mittelwerte mit 95%-Konfidenzgrenzen repräsentieren und
- Mittelwerte, denen ein gemeinsamer Buchstabe folgt, sich laut Tukey-Test nicht signifikant unterscheiden.
Zusammenfassung
Glückwunsch! Du hast deine erste Varianzanalyse und Mittelwertvergleiche für ein vollständig randomisiertes Versuchsdesign durchgeführt. Dies ist eine fundamentale Technik in der experimentellen Datenanalyse, die Sie in vielen verschiedenen Kontexten verwenden können.
Vollständig randomisiertes Versuchsdesign (CRD) ist das einfachste Versuchsdesign, bei dem Behandlungen zufällig den Versuchseinheiten zugeordnet werden.
-
Einfaktorielle ANOVA testet, ob es signifikante Unterschiede zwischen Gruppenmittelwerten gibt:
- Die Modellformel ist
response ~ factor - Die ANOVA-Tabelle zeigt, ob es insgesamt signifikante Unterschiede gibt
- Die Modellformel ist
-
Post-hoc-Tests bestimmen, welche spezifischen Gruppen sich voneinander unterscheiden:
- Geschätzte Randmittelwerte (emmeans) liefern adjustierte Mittelwerte für jede Gruppe
- Paarweise Vergleiche zwischen allen Mittelwerten/Gruppen werden durchgeführt
- Die kompakte Buchstabendarstellung (CLD) präsentiert Ergebnisse mit Buchstaben für einfache Interpretation
Im nächsten Kapitel werden wir das randomisierte vollständige Blockdesign (RCBD) erkunden, das auf dem CRD aufbaut, indem es bekannte Variationsquellen in Ihren Versuchseinheiten berücksichtigt.
Zitat
@online{schmidt2026,
author = {{Dr. Paul Schmidt}},
publisher = {BioMath GmbH},
title = {1. Einfaktorielle ANOVA in einem CRD},
date = {2026-02-08},
url = {https://biomathcontent.netlify.app/de/content/lin_mod_exp/01_oneway_crd.html},
langid = {de}
}