Um alle in diesem Kapitel verwendeten Pakete zu installieren und zu laden, kann man folgenden Code ausführen:
Statistische Modelle treffen Annahmen über die Daten, und Ergebnisse können irreführend sein, wenn diese Annahmen stark verletzt werden. Dieses Kapitel zeigt, wie man prüft, ob die Annahmen eines linearen Modells hinreichend erfüllt sind — ein Prozess, der als Modelldiagnostik bekannt ist. Wir beginnen mit einem schnellen, praktischen Ansatz und gehen dann schrittweise tiefer für diejenigen, die mehr Details wünschen.
Die Kurzversion
Man hat ein lineares Modell gefittet und möchte eigentlich nur die ANOVA-Ergebnisse — aber irgendwo in einer Vorlesung oder einem Lehrbuch wurde einem gesagt, man solle vorher “die Modellannahmen prüfen”. Verständlich. Hier ist der schnellste Weg, das zu tun und mit gutem Gewissen weiterzuarbeiten. Wir verwenden den integrierten PlantGrowth-Datensatz als Beispiel in diesem gesamten Kapitel:
mod <- lm(weight ~ group, data = PlantGrowth)Sowohl die PlantGrowth-Daten als auch die lm()-Funktion sind in R integriert und benötigen keine zusätzlichen Pakete. Nun erstellen wir die Standard-Diagnoseplots:
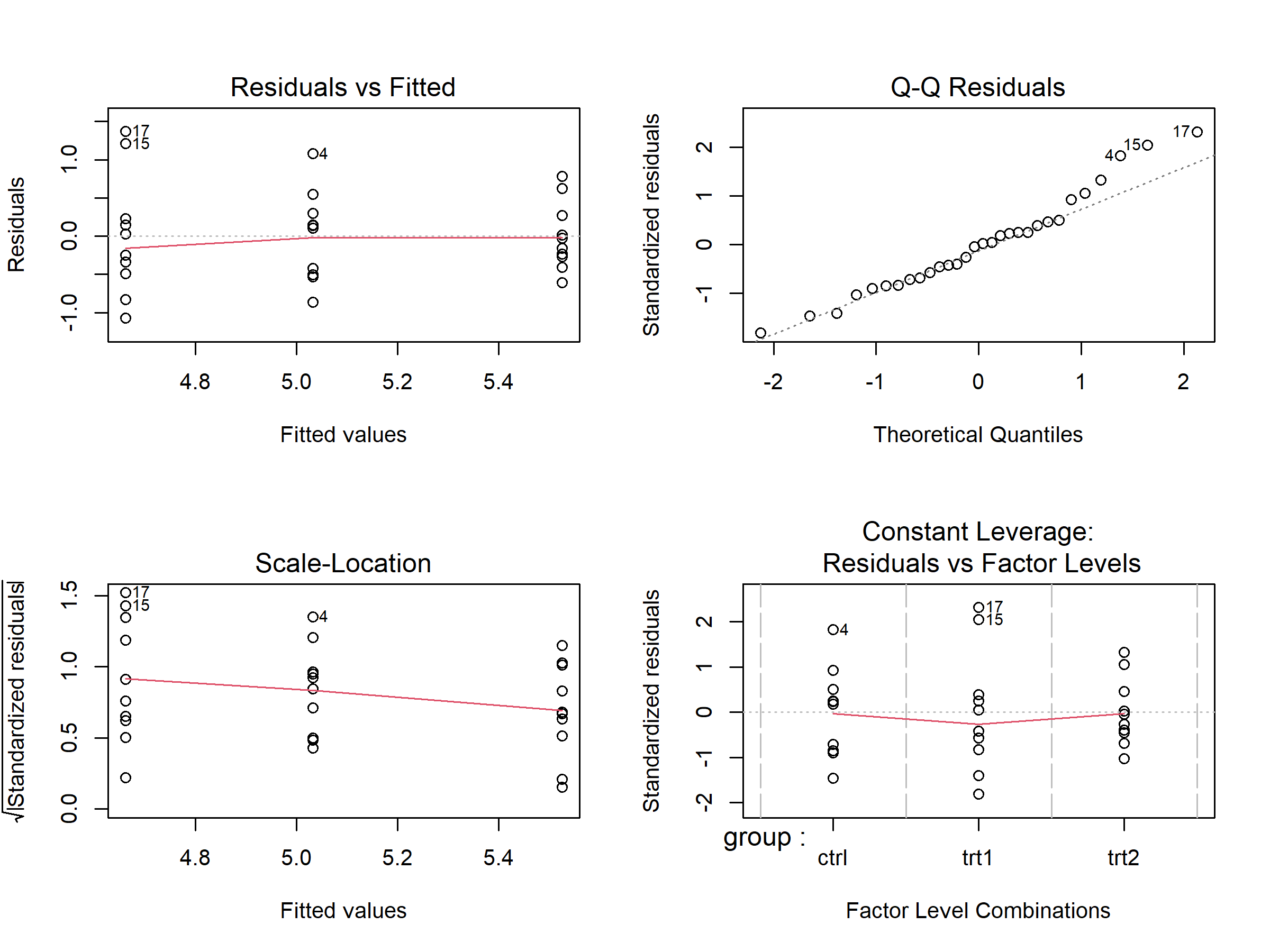
Die par(mfrow = ...)-Zeilen1 gehören nicht zur Diagnostik — plot(mod) ist der entscheidende Befehl. Diese vier Plots geben einen schnellen Überblick:
| Plot | Was prüfen? | Was ist in Ordnung? |
|---|---|---|
| Residuals vs Fitted (oben links) | Zufällige Streuung um Null? | Keine offensichtlichen Kurven oder Trichterformen |
| Q-Q Residuals (oben rechts) | Punkte nahe an der Diagonalen? | Die meisten Punkte folgen der Linie |
| Scale-Location (unten links) | Ungefähr gleichmäßige Streuung? | Kein deutlicher Trichter oder Trend |
| Residuals vs Factor Levels (unten rechts) | Extreme Ausreißer? | Keine Punkte weit jenseits der Cook’s-Distance-Linien |
Wenn die Plots ungefähr in Ordnung aussehen — keine dramatischen Muster, keine extremen Ausreißer — kann man mit der Analyse fortfahren. Lineare Modelle sind recht robust gegenüber kleinen Abweichungen von perfekten Annahmen. Wenn etwas deutlich problematisch aussieht, bieten die folgenden Abschnitte Orientierung.
Die {easystats}-Alternative
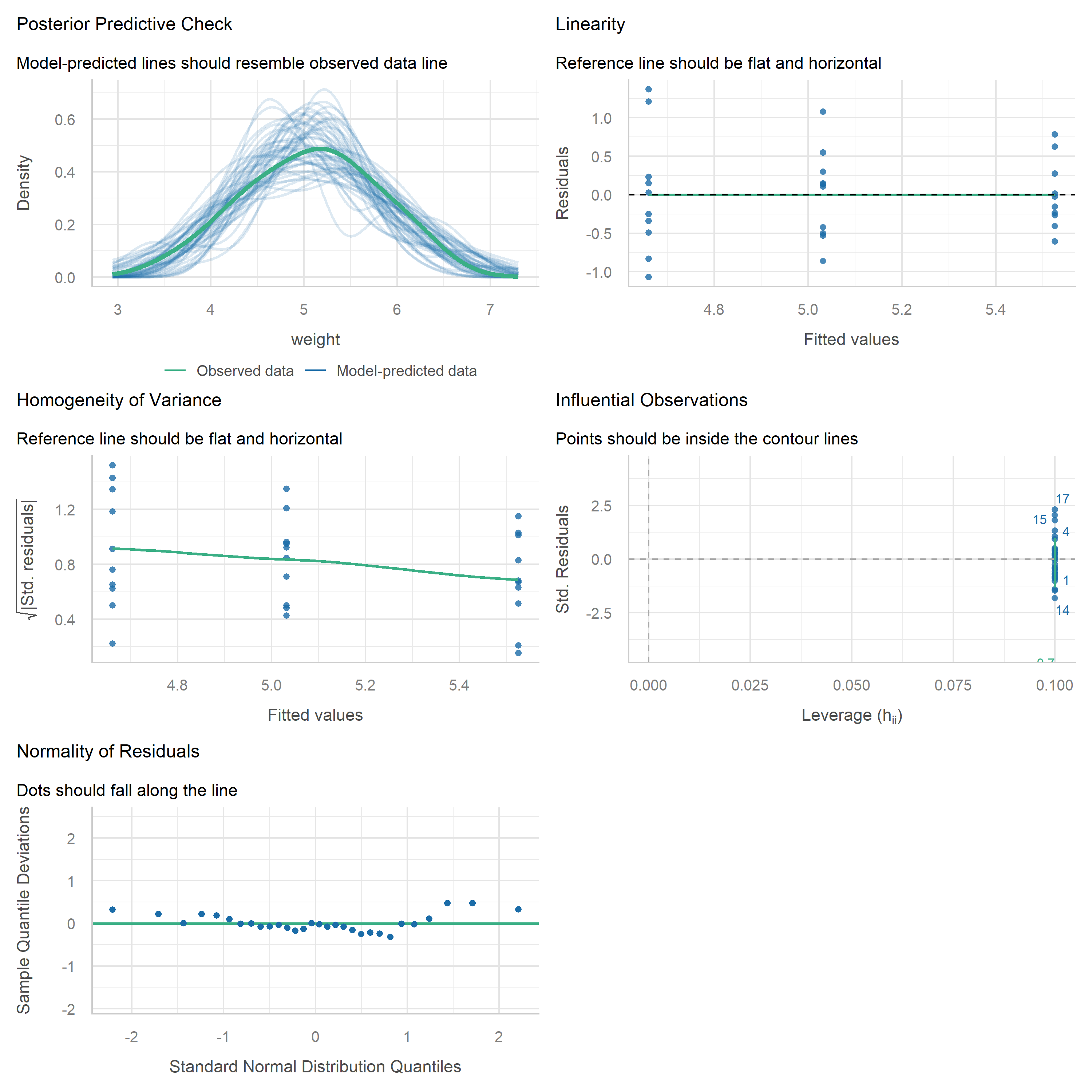
Wer einen umfassenderen Satz an Diagnoseplots in einem einzigen Aufruf haben möchte, findet im Paket {easystats} (das oben bereits geladen wurde) die Funktion check_model():
Diese Funktion erzeugt eine mehrteilige Abbildung, die die wichtigsten Annahmen abdeckt — einschließlich Normalverteilung, Homoskedastizität, einflussreiche Beobachtungen und Kollinearität — alles auf einmal. Es ist ein hervorragender Weg für einen schnellen und dennoch gründlichen Überblick, und die Plots sind wohl einfacher zu lesen als die Base-R-Versionen. Beide Ansätze eignen sich gut für die Routinediagnostik.
Die Annahmen verstehen
Lineare Modelle (einschließlich ANOVA) stützen sich auf mehrere Annahmen. Gehen wir jede einzelne durch und verstehen, worauf man achten muss.
Unabhaengigkeit
Annahme: Die einzelnen Beobachtungen sind voneinander unabhängig.
Diese Annahme lässt sich nicht mit Diagnoseplots oder statistischen Tests überprüfen. Stattdessen muss sie durch ein korrektes Versuchsdesign und Randomisierung sichergestellt werden. Wenn das Experiment ordnungsgemäß randomisiert wurde (wie es bei jeder gut geplanten Studie der Fall sein sollte), ist diese Annahme in der Regel erfüllt.
Wenn die Unabhängigkeit verletzt ist — beispielsweise bei Messwiederholungen über die Zeit, räumlich korrelierten Feldversuchen oder hierarchischen Datenstrukturen — werden die Standardfehler unzuverlässig. In solchen Fällen sollten stattdessen spezialisierte Methoden wie gemischte Modelle (Mixed-Effects Models) verwendet werden.
Normalverteilung der Residuen
Annahme: Die Modellresiduen folgen einer Normalverteilung.
Ein sehr häufiger Fehler ist es, zu prüfen, ob die rohe Zielvariable (z.B. Ertrag) normalverteilt ist. Darum geht es bei der Annahme aber nicht. Was annähernd normalverteilt sein muss, sind die Residuen des Modells — also die Abweichungen zwischen beobachteten und angepassten Werten. Siehe Kozak und Piepho (2018) (Abschnitt “4 | Answering Question 1”) für Details.
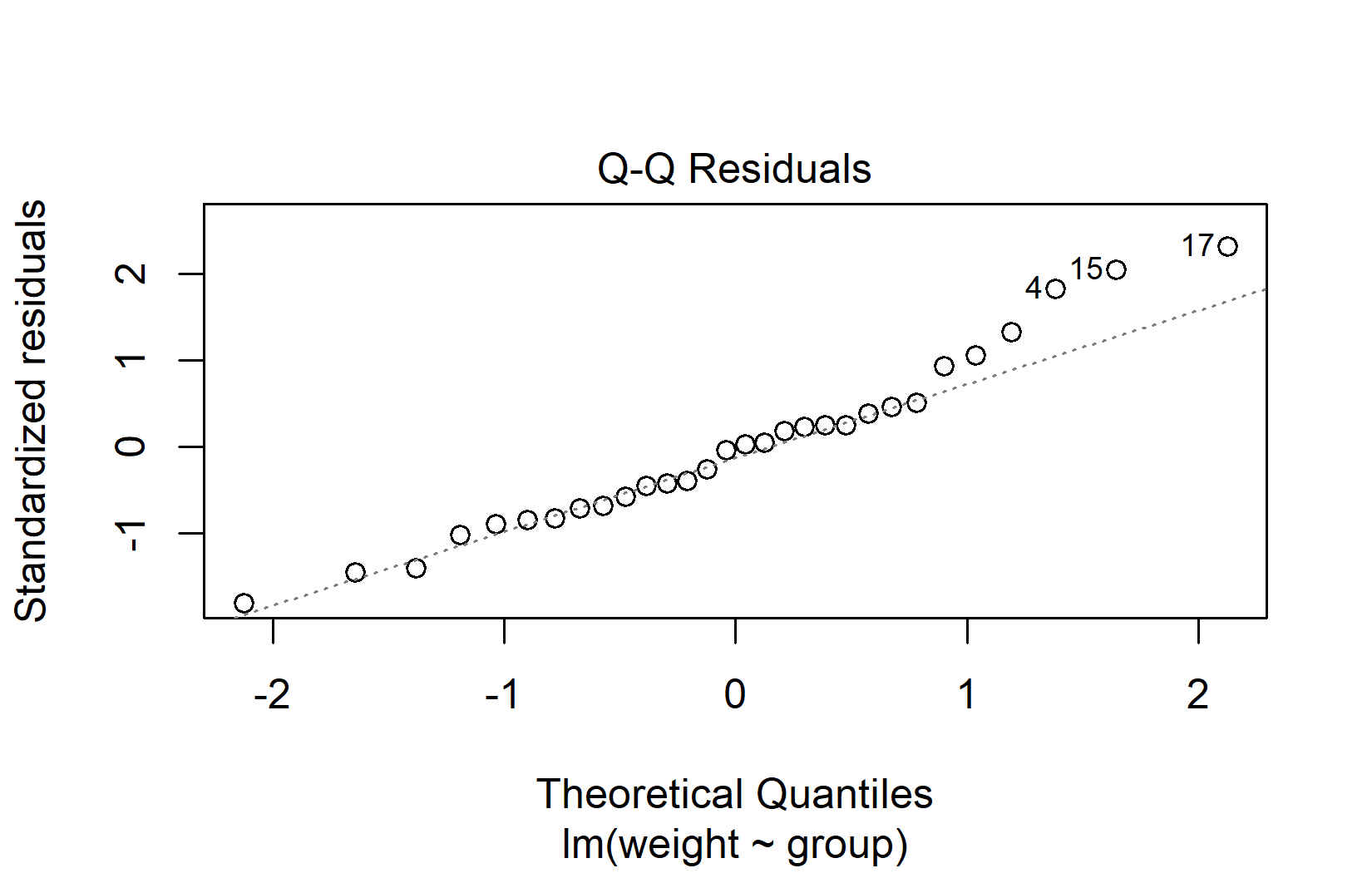
Der QQ-Plot (Quantil-Quantil-Plot) ist das primäre Werkzeug zur Beurteilung der Normalverteilung. Er stellt die Residuen den Werten gegenüber, die man bei perfekter Normalverteilung erwarten würde. Wenn die Normalverteilung gegeben ist, liegen die Punkte entlang der Diagonalen:
plot(mod, which = 2)Bei der Interpretation von QQ-Plots sollte man auf das Gesamtmuster achten, nicht auf einzelne Punkte:
- Gute Normalverteilung: Die Punkte folgen eng der Diagonalen, mit vielleicht kleinen Abweichungen an den äußersten Enden.
- Schwere Ränder (Heavy Tails): Die Punkte biegen an beiden Enden von der Linie ab (S-Form).
- Schiefe (Skewness): Die Punkte weichen systematisch in eine Richtung von der Linie ab.
- Ausreißer: Ein oder zwei Punkte weit von der Linie entfernt, während der Rest ihr gut folgt.
Kleine Abweichungen in QQ-Plots sind kein Grund zur Sorge. Lineare Modelle kommen gut mit leichter Nicht-Normalität zurecht, besonders bei ausreichenden Stichprobengrößen (ungefähr n > 15 pro Gruppe). Der Zentrale Grenzwertsatz stellt sicher, dass der ANOVA-F-Test auch bei nicht-normalen Residuen für moderate bis große Stichproben annähernd gültig bleibt.
Homoskedastizitaet
Annahme: Die Fehlervarianz ist über alle Gruppen / angepassten Werte konstant.
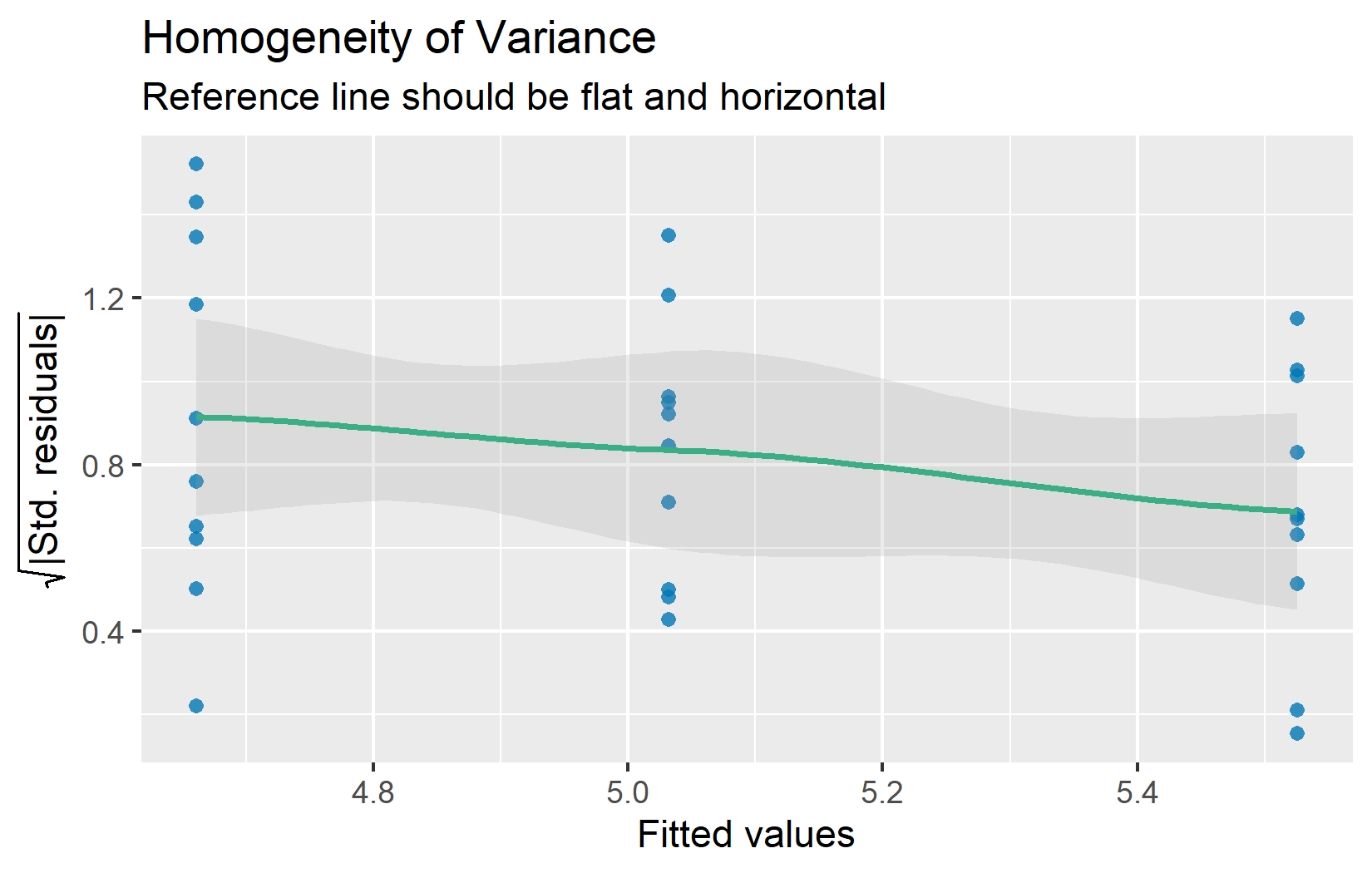
Auch als Homoskedastizität bezeichnet (das Gegenteil von Heteroskedastizität). Der Residuen-vs-Fitted-Plot hilft bei der Beurteilung dieser Annahme. Die Residuen sollten ein ungefähr gleichmäßiges horizontales Band um Null bilden:
Wenn die Streuung der Residuen mit den angepassten Werten deutlich zu- oder abnimmt (eine “Trichter”-Form), könnte die Varianzgleichheit verletzt sein. Geringe Unterschiede in der Streuung zwischen Gruppen sind in der Regel unproblematisch — die ANOVA ist recht robust, solange das Verhältnis der größten zur kleinsten Gruppenvarianz unter etwa 3:1 liegt.
Linearitaet
Annahme: Die Zielvariable lässt sich als Linearkombination der Prädiktoren darstellen.
Auch diese Annahme wird über den Residuen-vs-Fitted-Plot geprüft (das Panel oben links aus dem Vier-Panel-Plot oben). Bei jedem angepassten Wert sollte der Mittelwert der Residuen ungefähr Null sein. Wenn statt einer zufälligen Streuung ein deutlich gekrümmtes Muster zu erkennen ist, könnte die Linearitätsannahme nicht erfüllt sein.
Für Modelle mit ausschließlich kategorialen Prädiktoren (wie alle ANOVA-Beispiele in diesem Kurs) ist die Linearität automatisch erfüllt — das Modell schätzt einfach einen separaten Mittelwert für jede Gruppe. Die unten gezeigten Kurvenmuster können nur auftreten, wenn ein kontinuierlicher Prädiktor beteiligt ist (z.B. bei Regression). Dennoch ist es nützlich, diese Muster zu verstehen, da viele reale Analysen kategoriale und kontinuierliche Prädiktoren kombinieren.
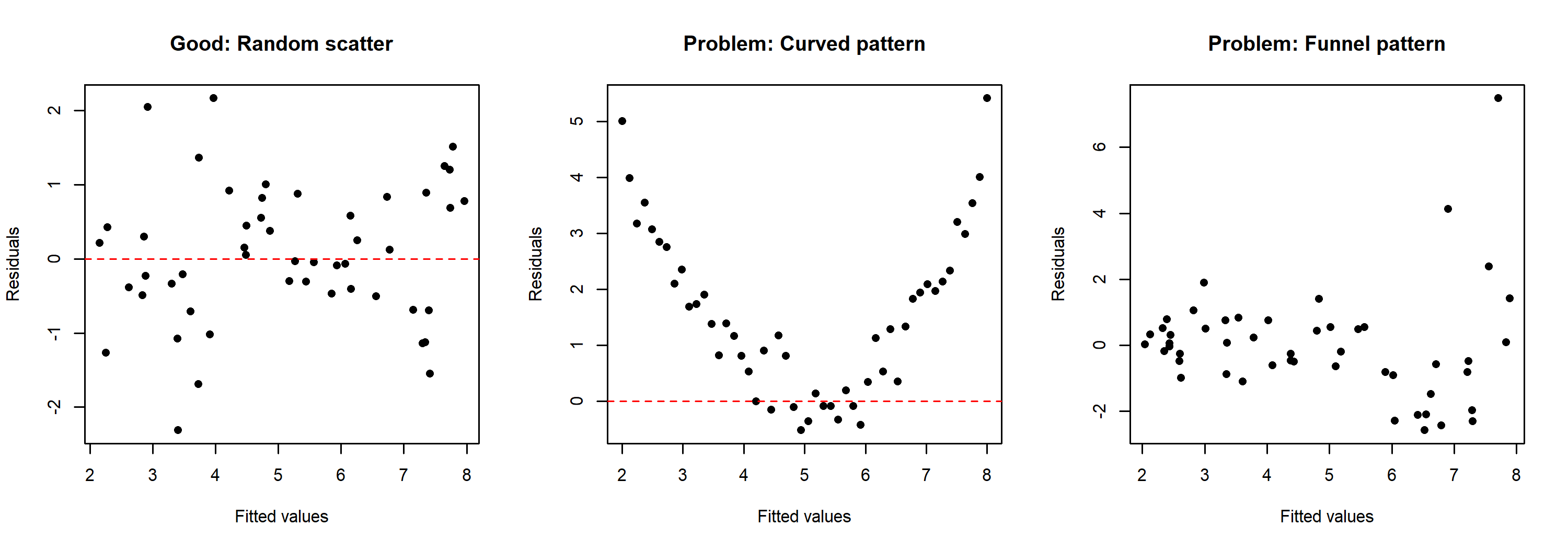
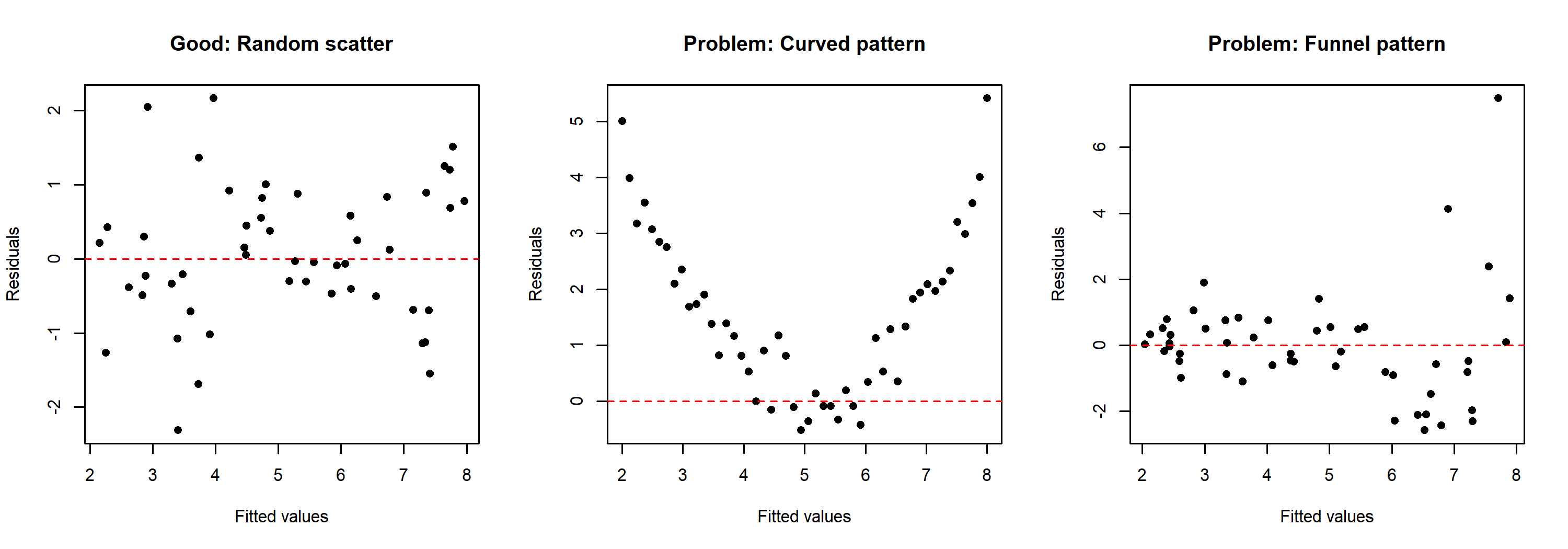
Um zu veranschaulichen, wie problematische Muster im Vergleich zu einem gesunden Residuenmuster aussehen, hier drei simulierte Beispiele:
Das linke Panel zeigt ein unauffälliges Residuenmuster mit zufälliger Streuung um Null. Das mittlere Panel zeigt ein gekrümmtes Muster, was darauf hindeutet, dass die Beziehung zwischen Prädiktor und Zielvariable nicht linear ist. Das rechte Panel zeigt ein Trichtermuster, bei dem die Streuung der Residuen mit den angepassten Werten zunimmt — dies deutet auf Heteroskedastizität hin und nicht auf ein Linearitätsproblem.
Vertiefung
Die vorangegangenen Abschnitte decken ab, was für die Routinediagnostik nötig ist. Was folgt, geht über die Grundlagen hinaus und behandelt differenziertere Fragen: Warum sind diagnostische Tests problematisch? Wie lassen sich einflussreiche Beobachtungen identifizieren? Und was kann man tun, wenn die Annahmen klar verletzt sind?
Warum Plots statt Tests?
Es mag naheliegend erscheinen, einen statistischen Test (wie den Shapiro-Wilk-Test auf Normalverteilung) zu verwenden, um die Annahmen “objektiv” zu prüfen. Allerdings gibt es einen wachsenden Konsens unter Statistikern, dass Diagnoseplots informativer sind als statistische Tests für diesen Zweck.
Kozak und Piepho (2018) liefern ein klares Argument, warum das so ist:
According to many authors (e.g., Atkinson, 1987; Belsley, Kuh, & Welsch, 2005; Kozak, 2009; Moser & Stevens, 1992; Quinn & Keough, 2002; Rasch, Kubinger, & Moder, 2011; Schucany & Ng, 2006), significance tests should not be used for checking assumptions. Diagnostic residual plots are a better choice.
[…]
There are two possible reasons for the overuse of statistical tests to check assumptions. First, many researchers base their knowledge on books first published 40 years ago or earlier. Back then, using statistical tests was relatively simple while using diagnostic plots was difficult; thus, these books advised the former, often even not mentioning the latter. Second, most statistical software offers statistical tests for checking assumptions as a default. Using default tests is simple, so users use them. However, we explained why we think that significance tests are not a good way of checking assumptions (in general, not only for ANOVA). First of all, with large samples (a very desirable situation) we risk that even small (and irrelevant) departures from the null hypothesis (which states that the assumption is met) will be detected as significant, and so we would need to reject the hypothesis and state that the assumption is not met. With small samples, the situation is opposite: much larger (and important) departures would not be found significant. Thus, our advice is to use diagnostic plots instead of hypothesis testing to check ANOVA assumptions.
Um dieses Problem in Aktion zu sehen, betrachten wir die Normalverteilungstests für unser Beispielmodell:
ols_test_normality(mod)-----------------------------------------------
Test Statistic pvalue
-----------------------------------------------
Shapiro-Wilk 0.9661 0.4379
Kolmogorov-Smirnov 0.1101 0.8215
Cramer-von Mises 3.6109 0.0000
Anderson-Darling 0.3582 0.4299
-----------------------------------------------Der QQ-Plot oben sieht völlig unauffällig aus, und dennoch sind sich die Tests nicht einig — man beachte, wie einzelne Tests eine “signifikante” Abweichung anzeigen können, obwohl der visuelle Eindruck klar akzeptabel ist. Diese widersprüchliche Situation illustriert genau, warum es irreführend sein kann, sich auf Tests statt auf visuelle Beurteilung zu verlassen.
Der Vollständigkeit halber hier die gängigen Tests auf Varianzhomogenität:
# Breusch-Pagan test
ols_test_breusch_pagan(mod)
Breusch Pagan Test for Heteroskedasticity
-----------------------------------------
Ho: the variance is constant
Ha: the variance is not constant
Data
----------------------------------
Response : weight
Variables: fitted values of weight
Test Summary
-----------------------------
DF = 1
Chi2 = 3.000303
Prob > Chi2 = 0.08324896 # Bartlett test (designed for comparing group variances)
bartlett.test(weight ~ group, data = PlantGrowth)
Bartlett test of homogeneity of variances
data: weight by group
Bartlett's K-squared = 2.8786, df = 2, p-value = 0.2371Beide sind nicht signifikant (p > 0,05), was mit den Diagnoseplots übereinstimmt. Aber zur Erinnerung: Ein nicht signifikanter Test garantiert nicht, dass die Annahme erfüllt ist — er könnte einfach unzureichende statistische Power widerspiegeln.
Ausreisser und einflussreiche Beobachtungen
Manchmal haben einzelne Beobachtungen einen unverhältnismäßig großen Einfluss auf die Modellergebnisse. Das sind nicht unbedingt fehlerhafte Datenpunkte, aber man sollte sich ihrer bewusst sein.
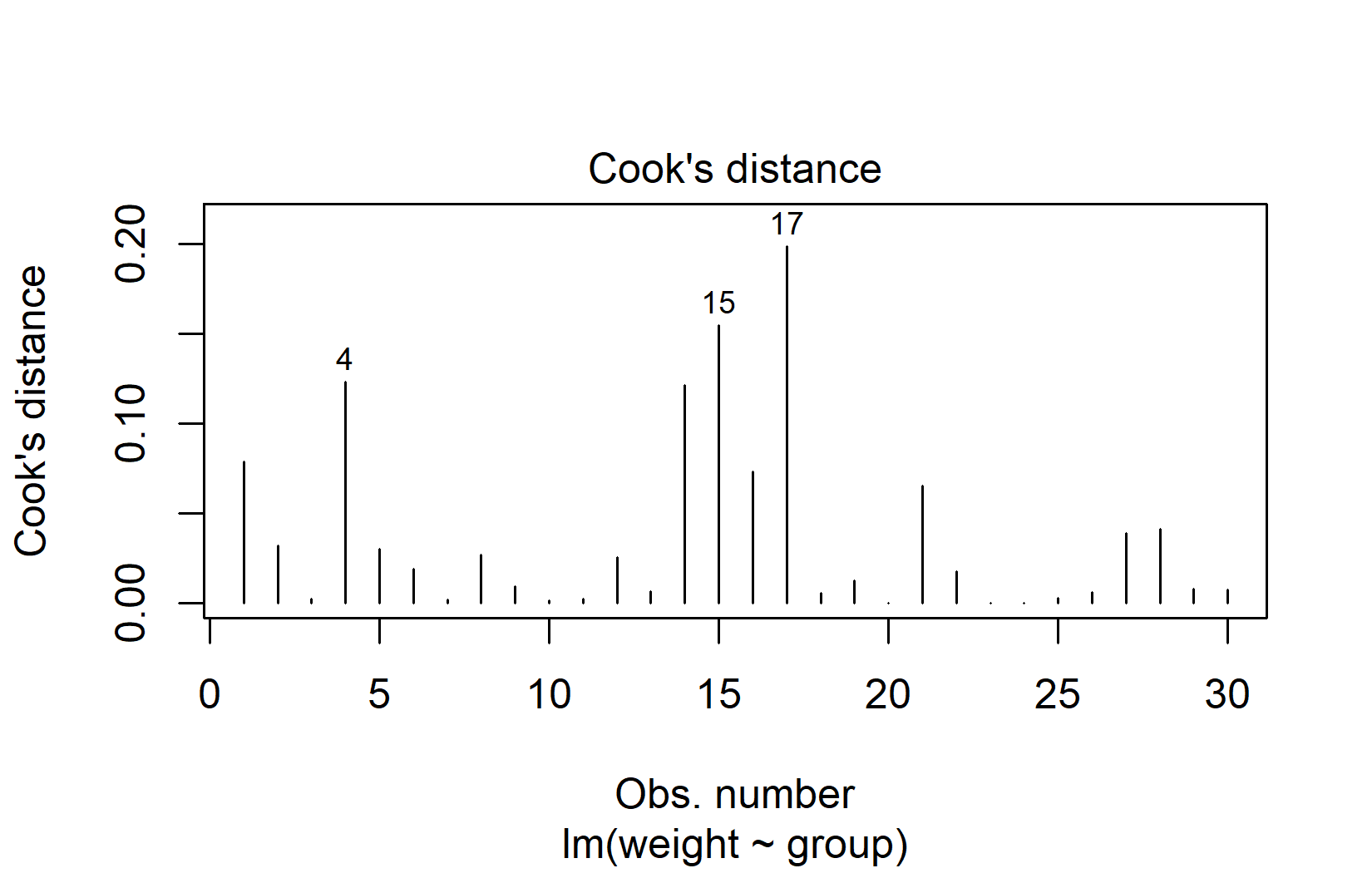
Cook’s Distance quantifiziert, wie stark sich alle angepassten Werte ändern, wenn eine einzelne Beobachtung entfernt wird. Eine gängige Faustregel: Beobachtungen mit Cook’s Distance größer als 4/n verdienen einen genaueren Blick:
plot(mod, which = 4)In unserem Beispiel haben die Beobachtungen 15 und 17 die höchste Cook’s Distance. Mit dem Schwellenwert bei 4/30 ≈ 0,13 liegen diese beiden Werte nur leicht darüber. Das ist recht mild — Cook’s-Distance-Werte über 1,0 würden auf ein ernsthaftes Problem hindeuten.
DFBETAS messen, wie stark sich jeder Regressionskoeffizient ändert, wenn eine einzelne Beobachtung entfernt wird. Beobachtungen mit |DFBETAS| > 2/√n verdienen Aufmerksamkeit. Wichtig ist, DFBETAS für alle Modellkoeffizienten zu prüfen, nicht nur den Intercept — eine Beobachtung könnte einen Gruppenkontrast stark beeinflussen, ohne den Gesamtmittelwert zu verändern:
n <- nrow(PlantGrowth)
db <- dfbetas(mod)
data.frame(
obs = 1:n,
cooks_d = round(cooks.distance(mod), 4),
dfb_intercept = round(db[, 1], 4),
dfb_grouptrt1 = round(db[, 2], 4),
dfb_grouptrt2 = round(db[, 3], 4)
) %>%
filter(
cooks_d > 4 / n |
if_any(starts_with("dfb_"), \(x) abs(x) > 2 / sqrt(n))
) obs cooks_d dfb_intercept dfb_grouptrt1 dfb_grouptrt2
1 1 0.0787 -0.4967 0.3512 0.3512
4 4 0.1231 0.6367 -0.4502 -0.4502
14 14 0.1215 0.0000 -0.4469 0.0000
15 15 0.1548 0.0000 0.5143 0.0000
17 17 0.1985 0.0000 0.5981 0.0000In der Praxis ist es am sinnvollsten, die Analyse sowohl mit als auch ohne die identifizierten einflussreichen Beobachtungen durchzuführen und die Schlussfolgerungen zu vergleichen. Stimmen sie überein, besteht kein Grund zur Sorge.
Was tun bei verletzten Annahmen?
Wenn Diagnoseplots klare Probleme aufzeigen, gibt es je nach Art und Schwere der Verletzung mehrere Möglichkeiten.
Datentransformation
Eine Transformation der Zielvariable mit einer mathematischen Funktion (z.B. Quadratwurzel oder Logarithmus) kann die Modelldiagnostik oft deutlich verbessern. Hier ein Beispiel mit Daten aus einem Gurkenversuch im Lateinischen Quadrat (dieselben Daten wie in Kapitel 3):
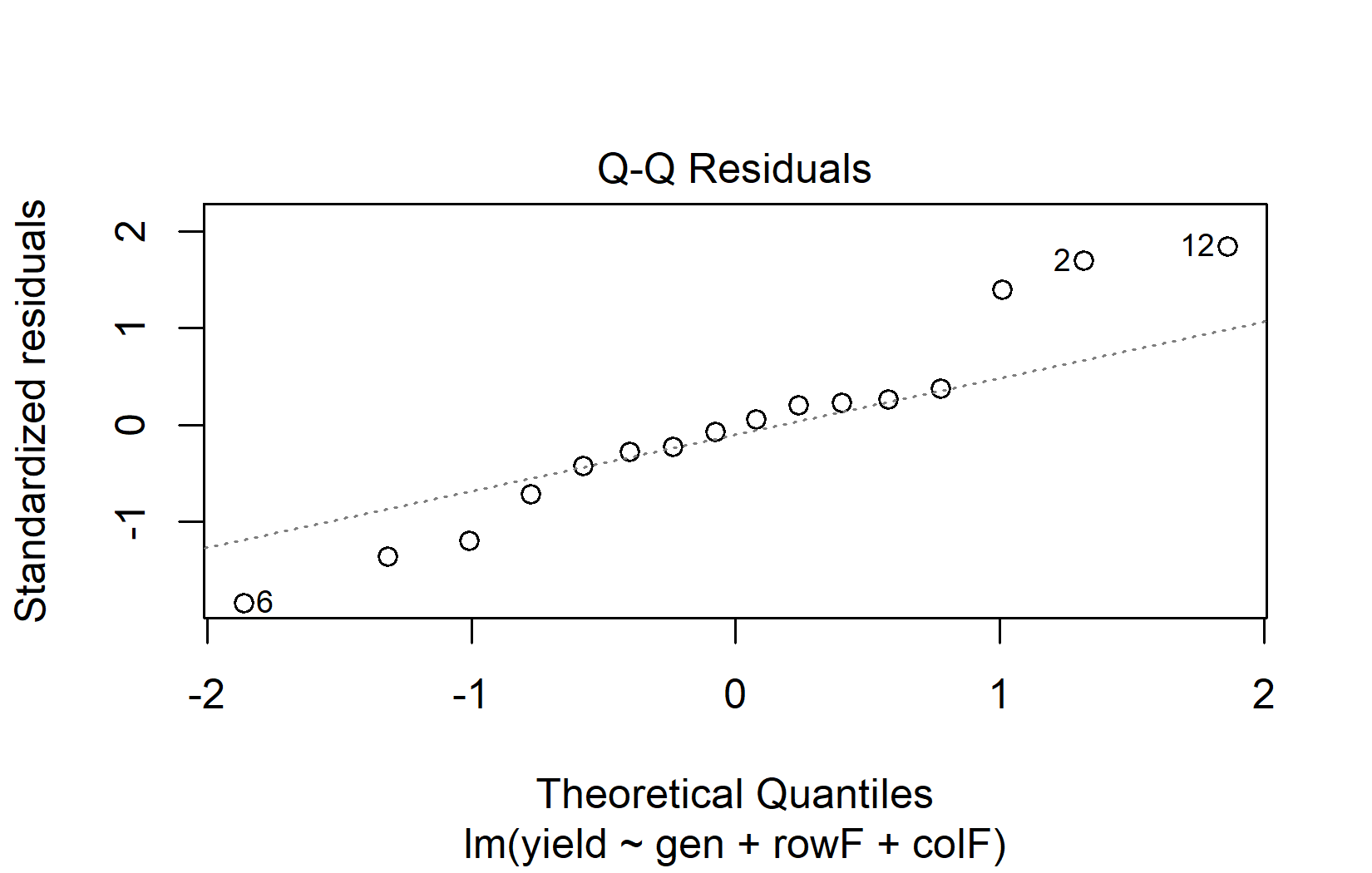
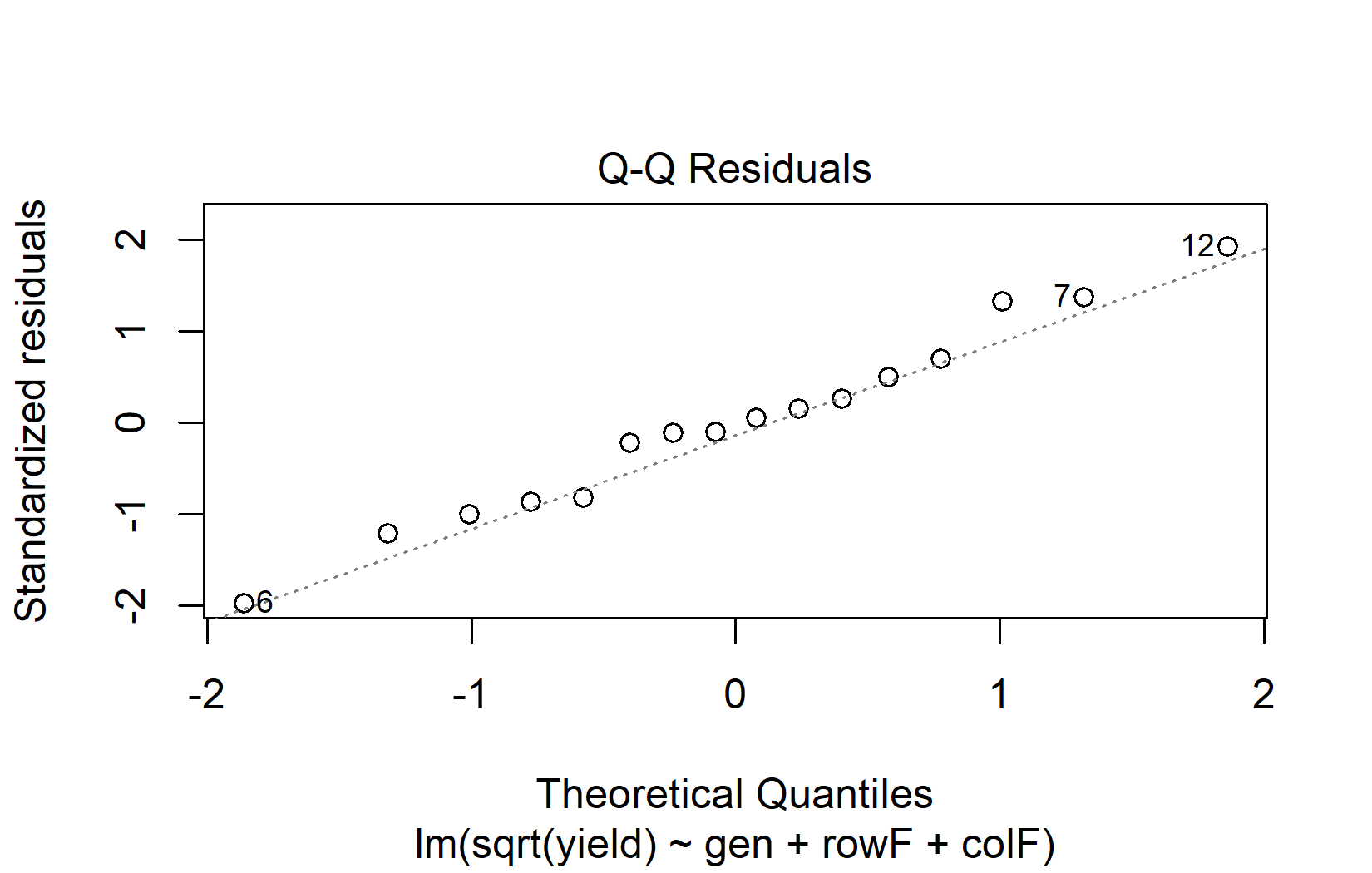
Wir fitten zwei Modelle — eines mit der ursprünglichen Zielvariable und eines mit der quadratwurzeltransformierten Zielvariable — und vergleichen ihre QQ-Plots nebeneinander:
Der QQ-Plot des Quadratwurzel-Modells liegt deutlich näher an der Diagonalen, daher fahren wir mit der ANOVA auf der transformierten Skala fort:
anova(mod_sqrt)Analysis of Variance Table
Response: sqrt(yield)
Df Sum Sq Mean Sq F value Pr(>F)
gen 3 10.5123 3.5041 8.8966 0.01256 *
rowF 3 5.0283 1.6761 4.2555 0.06228 .
colF 3 4.2121 1.4040 3.5647 0.08670 .
Residuals 6 2.3632 0.3939
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die ANOVA zeigt einen signifikanten Effekt des Genotyps. Für Mittelwertvergleiche mittels Post-hoc-Tests können die Mittelwerte auf der rücktransformierten (= ursprünglichen) Skala dargestellt werden, solange klar kommuniziert wird, dass Modellanpassung und Mittelwertvergleiche auf der Quadratwurzel-Skala durchgeführt wurden:
Note: adjust = "tukey" was changed to "sidak"
because "tukey" is only appropriate for one set of pairwise comparisons gen response SE df lower.CL upper.CL .group
Poinsett 20.9 2.87 6 12.0 32.1 a
Sprint 25.1 3.14 6 15.3 37.3 a
Guardian 30.4 3.46 6 19.5 43.7 ab
Dasher 45.3 4.23 6 31.7 61.4 b
Results are averaged over the levels of: rowF, colF
Confidence level used: 0.95
Conf-level adjustment: sidak method for 4 estimates
Intervals are back-transformed from the sqrt scale
Note: contrasts are still on the sqrt scale. Consider using
regrid() if you want contrasts of back-transformed estimates.
P value adjustment: tukey method for comparing a family of 4 estimates
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Hier bewirkt type = "response" die automatische Rücktransformation. Das funktioniert nur, wenn die Transformation innerhalb der Modellformel angegeben wird (wie hier mit sqrt(yield) in lm()), nicht wenn vorab eine transformierte Spalte erstellt wird.
Alternative Methoden (und ihre Grenzen)
Wenn die Annahmen verletzt sind und eine Transformation nicht hilft, gibt es verschiedene alternative Methoden. Wir stellen sie hier kurz vor, allerdings mit einem wichtigen Vorbehalt: Die meisten dieser Alternativen funktionieren nur für die einfachsten Versuchsdesigns.
Welch-ANOVA setzt keine gleichen Varianzen über die Gruppen voraus:
# Welch's ANOVA (does not assume equal variances)
oneway.test(weight ~ group, data = PlantGrowth, var.equal = FALSE)
One-way analysis of means (not assuming equal variances)
data: weight and group
F = 5.181, num df = 2.000, denom df = 17.128, p-value = 0.01739Robuste Standardfehler behalten das ursprüngliche Modell bei, passen aber die Standardfehler an, um Heteroskedastizität zu berücksichtigen:
for (pkg in c("lmtest", "sandwich")) {
if (!require(pkg, character.only = TRUE)) install.packages(pkg)
}
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.03200 0.19436 25.8896 < 2e-16 ***
grouptrt1 -0.37100 0.32828 -1.1301 0.26836
grouptrt2 0.49400 0.24401 2.0245 0.05291 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Nichtparametrische Tests wie der Kruskal-Wallis-Test lockern die Normalverteilungsannahme, indem sie mit Rängen statt mit Rohwerten arbeiten:
kruskal.test(weight ~ group, data = PlantGrowth)
Kruskal-Wallis rank sum test
data: weight by group
Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.01842Der Kruskal-Wallis-Test ist nicht vollkommen “annahmefrei” — er setzt weiterhin voraus, dass die Verteilungen in jeder Gruppe die gleiche Form haben, nur möglicherweise in ihrer Lage verschoben.
Alle drei oben gezeigten Methoden funktionieren gut für den hier demonstrierten einfachen einfaktoriellen Fall. In der Praxis haben die meisten Experimente jedoch mehrere Behandlungsfaktoren, Blockstrukturen oder zufällige Effekte — und genau dort stoßen diese Alternativen an ihre Grenzen:
- Welch-ANOVA funktioniert nur für einfaktorielle Designs. Es gibt keine Welch-Version für zweifaktorielle ANOVA, Split-Plot-Designs oder Modelle mit Blockeffekten.
- Robuste Standardfehler lassen sich breiter anwenden, aber Standardimplementierungen erstrecken sich nicht sauber auf gemischte Modelle oder komplexe Varianzstrukturen.
- Nichtparametrische Tests existieren für einige wenige einfache Designs — Kruskal-Wallis für einfaktorielle Anordnungen, der Friedman-Test für RCBD — aber es gibt keine einfachen nichtparametrischen Entsprechungen für faktorielle Designs, unvollständige Blockdesigns oder Split-Plot-Versuche.
In der Praxis bedeutet das: Für die meisten der in diesem Kurs behandelten Versuchsdesigns (Lateinisches Quadrat, Alpha-Design, Row-Column usw.) sind diese Alternativen in der Regel nicht verfügbar. Die realistischen Optionen bei verletzten Annahmen in komplexen Designs sind: (1) Datentransformation, (2) Verwendung generalisierter linearer Modelle (GLMs — siehe den Ausblick unten) oder (3) Akzeptieren, dass milde Verletzungen kein Problem darstellen (siehe die Robustheitsdiskussion unten).
Wie robust sind lineare Modelle?
Lineare Modelle sind robuster gegenüber Annahmenverletzungen, als häufig gelehrt wird. Die Forschung hat durchgängig gezeigt:
- ANOVA ist robust gegenüber moderaten Verletzungen sowohl der Normalverteilung als auch der Varianzhomogenität, besonders bei balancierten und ausreichenden Stichprobengrößen.
- Der Zentrale Grenzwertsatz stellt sicher, dass Teststatistiken auch bei nicht-normalen Residuen mit wachsenden Stichprobengrößen gegen ihre erwarteten Verteilungen konvergieren.
- Leichte Verletzungen sind die Norm, nicht die Ausnahme. Die meisten realen Daten weichen in gewissem Maße von perfekten Annahmen ab.
Als grobe Richtlinie:
| Stichprobengröße pro Gruppe | Praktischer Rat |
|---|---|
| Klein (n < 15) | Annahmenverletzungen wirken sich stärker aus. Exakte Tests oder robuste Methoden in Betracht ziehen. Diagnostik sorgfältig interpretieren. |
| Moderat (15–50) | Standard-ANOVA ist in der Regel robust bei milden Verletzungen. Nur schwerwiegende Probleme suchen. |
| Groß (50+) | Der Zentrale Grenzwertsatz bietet starken Schutz. Annahmenprüfung ist weniger kritisch, aber Diagnoseplots können dennoch Datenqualitätsprobleme aufdecken. |
Die Kernbotschaft: Man sollte ANOVA-Ergebnisse nicht wegen kleiner Unvollkommenheiten in Diagnoseplots verwerfen. Der Fokus liegt auf klaren, eindeutigen Verletzungen. Im Zweifel kann man die Analyse sowohl mit dem Standardansatz als auch mit einer robusten Alternative durchführen — stimmen die Schlussfolgerungen überein, war die Annahmenverletzung nicht folgenreich.
Allgemein
- What’s normal anyway? Residual plots are more telling than significance tests when checking ANOVA assumptions (Kozak und Piepho 2018)
- Chapter 13 Model Diagnostics in Applied Statistics with R (Dalpiaz, 2022)
- {olsrr} R-Paket-Dokumentation
Normalverteilung
- Für diesen speziellen Zweck werden QQ-Plots auch als Normal probability plots bezeichnet
Varianzhomogenität
Transformation
- Kapitel 3.3 in Dormann und Kühn (2011)
Ausblick: Generalisierte Lineare Modelle
Bisher hat sich dieses Kapitel mit Situationen befasst, in denen die Annahmen eines linearen Modells annähernd erfüllt sind oder milde Verletzungen toleriert werden können. Aber was ist mit Daten, die diese Annahmen grundsätzlich nicht erfüllen können?
Man denke an Zähldaten (z.B. Anzahl Insekten pro Pflanze) oder Anteile (z.B. Prozentsatz gekeimter Samen). Diese Zielvariablen sind inhärent nicht-normal: Zähldaten sind diskret und können nicht negativ sein, Anteile liegen zwischen 0 und 1. Transformationen (wie Logarithmus für Zähldaten oder Arcussinus-Quadratwurzel für Anteile) werden seit Jahrzehnten verwendet und können helfen, lösen aber die grundsätzliche Diskrepanz zwischen den Daten und der Normalverteilung nicht vollständig auf. Der Versuch, solche Daten in ein Standard-Linearmodell zu zwängen, führt häufig zu persistenten Diagnostikproblemen — und das ist ein Zeichen, dass das Modell selbst möglicherweise nicht das richtige Werkzeug für die Aufgabe ist.
Generalisierte Lineare Modelle (GLMs) lösen dieses Problem, indem sie den Rahmen linearer Modelle erweitern, um verschiedene Typen von Zielvariablen direkt zu verarbeiten. Anstatt normalverteilte Residuen vorauszusetzen, erlaubt ein GLM die Spezifikation einer Verteilung, die zur Natur der Daten passt:
| Datentyp | Verteilung | Beispiel |
|---|---|---|
| Zähldaten (0, 1, 2, …) | Poisson | Anzahl Insekten pro Parzelle |
| Binäre Ergebnisse (ja/nein) | Binomial | Gekeimt oder nicht |
| Anteile (0–1) | Beta oder Binomial | Infektionsrate |
| Positive stetige Daten | Gamma | Ertrag mit Rechtsschiefe |
Das Elegante an GLMs ist, dass die Modellannahmen um den tatsächlichen datengenerierenden Prozess herum aufgebaut sind, anstatt die Daten in einen normalen Rahmen zu zwängen. Wenn also Diagnoseplots systematische Probleme zeigen, die eine Transformation nicht beheben kann, lautet die Antwort oft nicht “die Annahmen stärker erfüllen”, sondern “ein Modell verwenden, dessen Annahmen zu den Daten passen”.
GLMs verwenden dieselbe R-Syntax, die man bereits kennt — glm() statt lm() — und sie integrieren sich mit denselben Werkzeugen für ANOVA-artige Auswertung (anova(), emmeans()), Blockstrukturen und faktorielle Designs. Eine ausführliche Behandlung von GLMs geht über den Rahmen dieses Kapitels hinaus, aber es ist gut zu wissen, dass sie als prinzipientreue Lösung für Daten existieren, die nicht in den Rahmen linearer Modelle passen.
Mit
plot(mod)beginnen — der Vier-Panel-Diagnoseplot bietet eine schnelle visuelle Prüfung der wichtigsten Annahmen. Alternativ kann mancheck_model(mod)aus {easystats} für einen umfassenderen Überblick verwenden.Plots statt Tests zur Annahmenprüfung verwenden. Statistische Tests auf Normalverteilung oder Varianzhomogenität führen oft in die Irre, besonders bei kleinen oder großen Stichproben.
Residuen prüfen, nicht Rohdaten. Die Normalverteilung muss an den Modellresiduen beurteilt werden, nicht an der Zielvariable.
Leichte Verletzungen sind meist kein Problem. Lineare Modelle sind robust, besonders bei ausreichenden Stichprobengrößen.
Bei schweren Verletzungen ist die Datentransformation in der Regel das erste und am breitesten anwendbare Mittel.
Alternative Methoden haben Grenzen. Welch-ANOVA, robuste Standardfehler und nichtparametrische Tests funktionieren nur für die einfachsten Designs. Für komplexe Versuche kommen Transformation oder GLMs in Frage.
Transparent berichten. Den Diagnostikprozess und alle getroffenen Maßnahmen dokumentieren.
Literatur
Fußnoten
par(mfrow = c(2, 2))ist ein R-Base-Graphics-Befehl, der die nächsten Plots in einem 2x2-Raster anordnet. Er hat nichts mit Modelldiagnostik zu tun — er teilt R lediglich mit, vier Plots gleichzeitig statt nacheinander anzuzeigen. Daspar(mfrow = c(1, 1))am Ende setzt das Layout wieder auf die Standard-Einzelansicht zurück.↩︎
Zitat
@online{schmidt2026,
author = {{Dr. Paul Schmidt}},
title = {A1. Modelldiagnostik},
date = {2026-02-08},
url = {https://biomathcontent.netlify.app/de/content/lin_mod_exp/a1_modeldiagnostics.html},
langid = {de}
}