# Pakete installieren (nur nötig, falls noch nicht installiert)
for (pkg in c("here", "readxl", "tidyverse")) {
if (!require(pkg, character.only = TRUE)) install.packages(pkg)
}
# Pakete laden
library(tidyverse)
library(here)
library(readxl)Um alle in diesem Kapitel verwendeten Pakete zu installieren und zu laden, führe den folgenden Code aus:
Daten
Dieser Datensatz enthält Informationen von zwei Landwirten, Max und Peter, die unterschiedliche Mengen Dünger auf ihre Felder ausbrachten und den resultierenden Ertragszuwachs im Vergleich zu ungedüngten Kontrollparzellen aufzeichneten1.
Import
dat <- read_csv(
file = here("data", "yield_increase.csv")
)
datRows: 20 Columns: 3
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): farmer
dbl (2): fert, yield_inc
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.# A tibble: 20 × 3
farmer fert yield_inc
<chr> <dbl> <dbl>
1 Max 1 0.2
2 Max 2 0.3
3 Max 3 0.5
4 Max 3 0.6
5 Max 4 0.6
6 Max 4 0.5
7 Max 4 0.7
8 Max 5 0.6
9 Max 7 0.8
10 Max 8 1
11 Peter 1 0.1
12 Peter 1 0.1
13 Peter 1 0.2
14 Peter 1 0.2
15 Peter 1 0.1
16 Peter 3 0.3
17 Peter 5 0.5
18 Peter 6 0.8
19 Peter 8 0.9
20 Peter 9 1.3Ziel
Das Ziel dieser Analyse ist es, die Frage zu beantworten, wie die Düngerausbringung mit der Ertragssteigerung zusammenhängt. Man kann dabei die Spalte farmer ignorieren, da es nicht wichtig ist, ob die Daten von Peter oder Max stammen. Wir konzentrieren uns daher nur auf die beiden numerischen Spalten fert und yield_inc. Für diese führen wir eine Korrelations- und eine Regressionsanalyse durch.
Exploration
Um diesen Datensatz zu erkunden, kann man zunächst einen schnellen Blick auf die Daten werfen mit
summary(dat) farmer fert yield_inc
Length:20 Min. :1.00 Min. :0.100
Class :character 1st Qu.:1.00 1st Qu.:0.200
Mode :character Median :3.50 Median :0.500
Mean :3.85 Mean :0.515
3rd Qu.:5.25 3rd Qu.:0.725
Max. :9.00 Max. :1.300 um zu erfahren, dass die ausgebrachte Düngermenge von 1 bis 9 kg/ha reicht mit einem Mittelwert von etwa 3,7 kg/ha, während die gemessenen Ertragssteigerungen von 0,1 bis 1,3 Tonnen/ha reichen mit einem Mittelwert von etwa 0,5 Tonnen/ha.
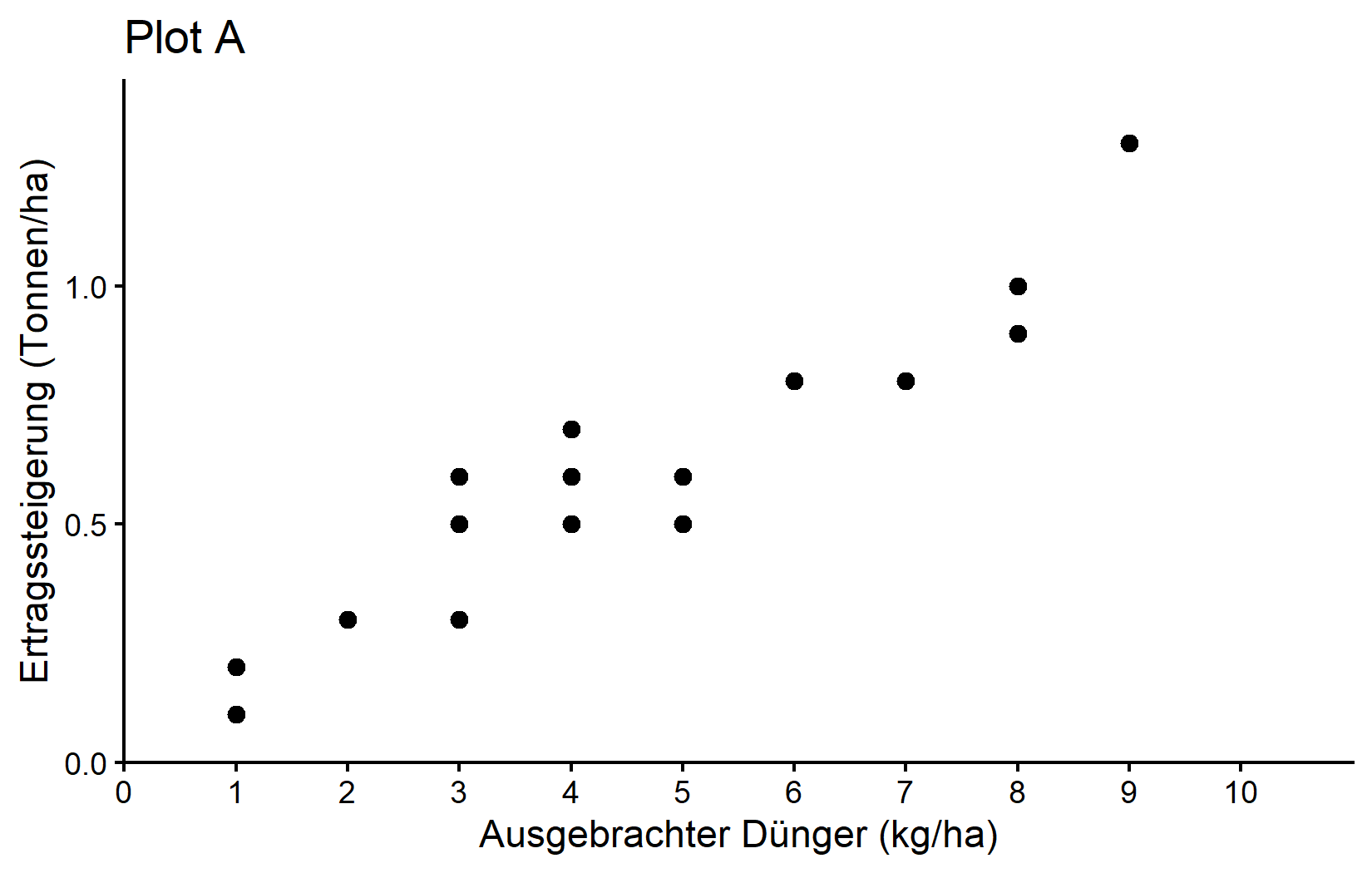
Und nun ist es endlich Zeit, unseren ersten ggplot zu erstellen. Unser Ziel ist es, ihn so zu erstellen:
Die Grafik zeigt einen klaren Trend steigender Ernteerträge bei höherer Düngerausbringung - was wir erwarten würden.
Um den Code zu sehen und zu verstehen, der für die Erstellung dieses ggplots und aller anderen ggplots in diesem Kapitel benötigt wird, gehe zum nächsten Kapitel. Man kann dies jetzt tun oder nach dem Lesen dieses Kapitels.
Korrelation
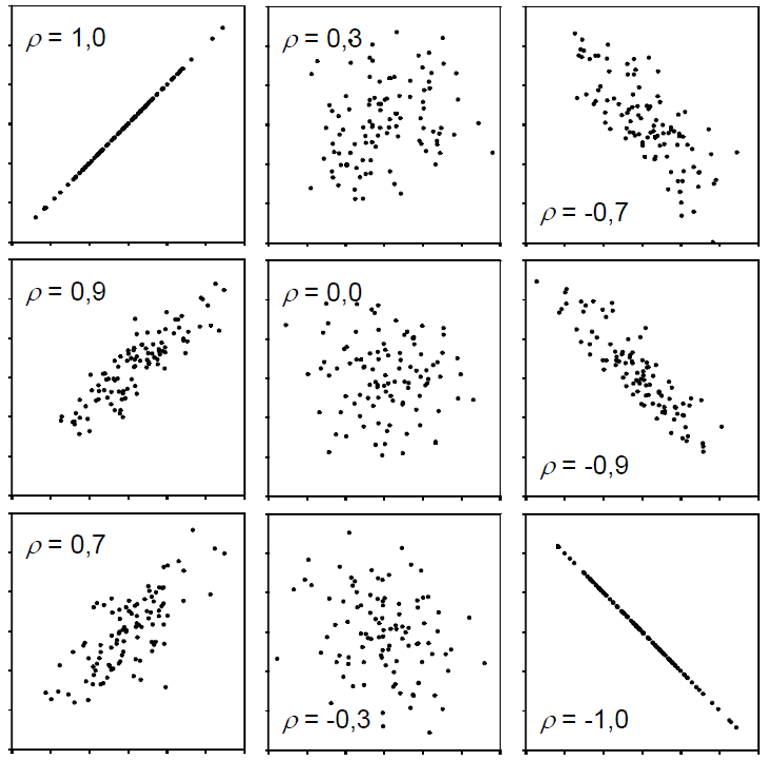
Eine Möglichkeit, tatsächlich eine Zahl für diesen Zusammenhang zu ermitteln, ist die Schätzung der Korrelation. Wenn Leute in der Statistik über Korrelation (\(\rho\) oder \(r\)) sprechen, meinen sie normalerweise den Pearson-Korrelationskoeffizienten, der ein Maß für die lineare Korrelation zwischen zwei numerischen Variablen ist. Korrelation kann nur Werte zwischen -1 und 1 haben, wobei 0 keine Korrelation bedeutet, während alle anderen möglichen Werte entweder negative oder positive Korrelationen sind. Je weiter von 0 entfernt, desto stärker ist die Korrelation. Hier sind einige Beispiele:
Einfach ausgedrückt bedeutet eine positive Korrelation “wenn eine Variable größer wird, wird die andere auch größer” und eine negative Korrelation bedeutet “wenn eine Variable größer wird, wird die andere kleiner”. Daher spielt es keine Rolle, welche der beiden Variablen die erste (“x”) oder die zweite (“y”) Variable ist. Außerdem ist eine Korrelationsschätzung nicht wie ein Modell und kann keine Vorhersagen treffen. Schließlich bedeutet “Korrelation impliziert keine Kausalität”, dass man nur weil man eine (starke) Korrelation zwischen zwei Dingen gefunden hat, nicht schließen kann, dass es einen Ursache-Wirkungs-Zusammenhang zwischen den beiden gibt.
- Schau dir diese Scheinkorrelationen für einige lustige Beispiele von Korrelation ohne Kausalität an.
- Spiele mit diesem praktischen Tool herum, um ein besseres Gefühl für den Zusammenhang zwischen Korrelation und Daten zu bekommen.
Berechnung
Wenn man nur die tatsächliche Korrelationsschätzung erhalten möchte, kann man die Funktion cor() verwenden und die beiden numerischen Variablen (als Vektoren) bereitstellen. In unserem Fall können wir die Spalte mit der Düngerausbringung aus unserem Datenobjekt dat mit dat$fert extrahieren und die Spalte mit der Ertragssteigerung mit dat$yield_inc. Zur Erinnerung: Das $-Zeichen kann verwendet werden, um eine Spalte aus einer Tabelle zu extrahieren. Der Befehl zur Ermittlung der Korrelation zwischen Düngerausbringung und Ertragssteigerung sieht also so aus:
cor(dat$fert, dat$yield_inc)[1] 0.9559151Dementsprechend ist die Korrelation zwischen Düngerausbringung und Ertragssteigerung in unserer Stichprobe sehr stark, da sie nahe bei 1 liegt. Dies deutet darauf hin, dass eine Erhöhung des Düngers tendenziell mit einer Erhöhung des Ernteertrags verbunden ist.
Test
Wenn man zusätzliche Informationen wie ein Konfidenzintervall und einen Test mit einem p-Wert haben möchte, kann man stattdessen cor.test() verwenden.
mycor <- cor.test(dat$fert, dat$yield_inc)
mycor
Pearson's product-moment correlation
data: dat$fert and dat$yield_inc
t = 13.811, df = 18, p-value = 5.089e-11
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8897837 0.9827293
sample estimates:
cor
0.9559151 Das Thema Hypothesentests, p-Werte und statistische Signifikanz ist etwas komplexer und hat ein eigenes Kapitel. Man kann es jetzt oder nach diesem Kapitel lesen.
Bei diesem längeren Output kann man die Stichprobenschätzung unten sehen, ein Konfidenzintervall darüber und einen p-Wert mit der entsprechenden Testhypothese darüber. Führe ?cor.test() aus und schaue dir den Abschnitt “Details” für weitere Informationen an. Hier ist unsere Korrelationsschätzung signifikant von 0 verschieden, da der p-Wert viel kleiner als 0,05 ist. Außerdem bedeutet das gezeigte Konfidenzintervall, dass wir zu 95% sicher sind, dass die wahre Korrelation irgendwo in diesem Bereich liegt.
Menschen würden dies in ihrem Ergebnisabschnitt berichten als z.B. “Die Korrelation zwischen Düngerausbringung und Ertragssteigerung betrug 0,96 (95% KI: 0,89, 0,98) und war statistisch signifikant (p < 0,001).”
Einfache lineare Regression
Wenn Leute in der Statistik über Regression sprechen, meinen sie normalerweise die einfache lineare Regression, die - einfach ausgedrückt - die beste gerade Linie findet, die durch Punkte in einem Streudiagramm von zwei numerischen Variablen geht.
Das lineare Modell hinter einer solchen geraden Linie ist einfach:
\[ y = \alpha + \beta x\]
wobei \(\alpha\) oder \(a\) der Achsenabschnitt und \(\beta\) oder \(b\) die Steigung ist, während \(y\) und \(x\) unsere Datenpunkte sind. Eine solche Regression anzupassen bedeutet wirklich nur, die optimalen Schätzungen für \(\alpha\) und \(\beta\) zu finden.
Im Gegensatz zur Korrelation ist eine einfache lineare Regression ein Modell und es ist daher wichtig, welche Variable \(y\) (abhängige Variable) und welche \(x\) (unabhängige) ist, denn nach der Anpassung der Regression kann letztere verwendet werden, um erstere vorherzusagen.
Besuche diese Website, gib “y=a+bx” in das Feld oben links ein, drücke Enter und spiele dann mit den Werten von \(a\) und \(b\) in den Feldern darunter herum. Man kann sehen, wie das Ändern der Steigung und des Achsenabschnitts die Linie verändert. Die Steigung (\(b\)) gibt an, um wie viel \(y\) zunimmt, wenn \(x\) um 1 Einheit zunimmt, während der Achsenabschnitt (\(a\)) den erwarteten Wert von \(y\) angibt, wenn \(x\) gleich 0 ist.
Berechnung
In R können wir die Funktion lm() für die Anpassung linearer Modelle verwenden, sodass sie die oben gezeigte einfache lineare Regressionsgleichung einfach anpasst:
reg <- lm(formula = yield_inc ~ fert,
data = dat)Wie man sehen kann, verweisen wir auf unser Datenobjekt dat im data = Argument, sodass wir im formula = Argument nur die Namen der jeweiligen Spalten in dat schreiben müssen. Außerdem speichern wir die Ergebnisse im reg Objekt. Wenn wir uns dieses Objekt ansehen, erhalten wir die folgenden Ergebnisse:
reg
Call:
lm(formula = yield_inc ~ fert, data = dat)
Coefficients:
(Intercept) fert
0.04896 0.12105 Zuerst wird unser Befehl wiederholt und dann werden die “Coefficients” gezeigt, die tatsächlich die Schätzungen für \(a\) und \(b\) sind. Die beste gerade Linie ist also:
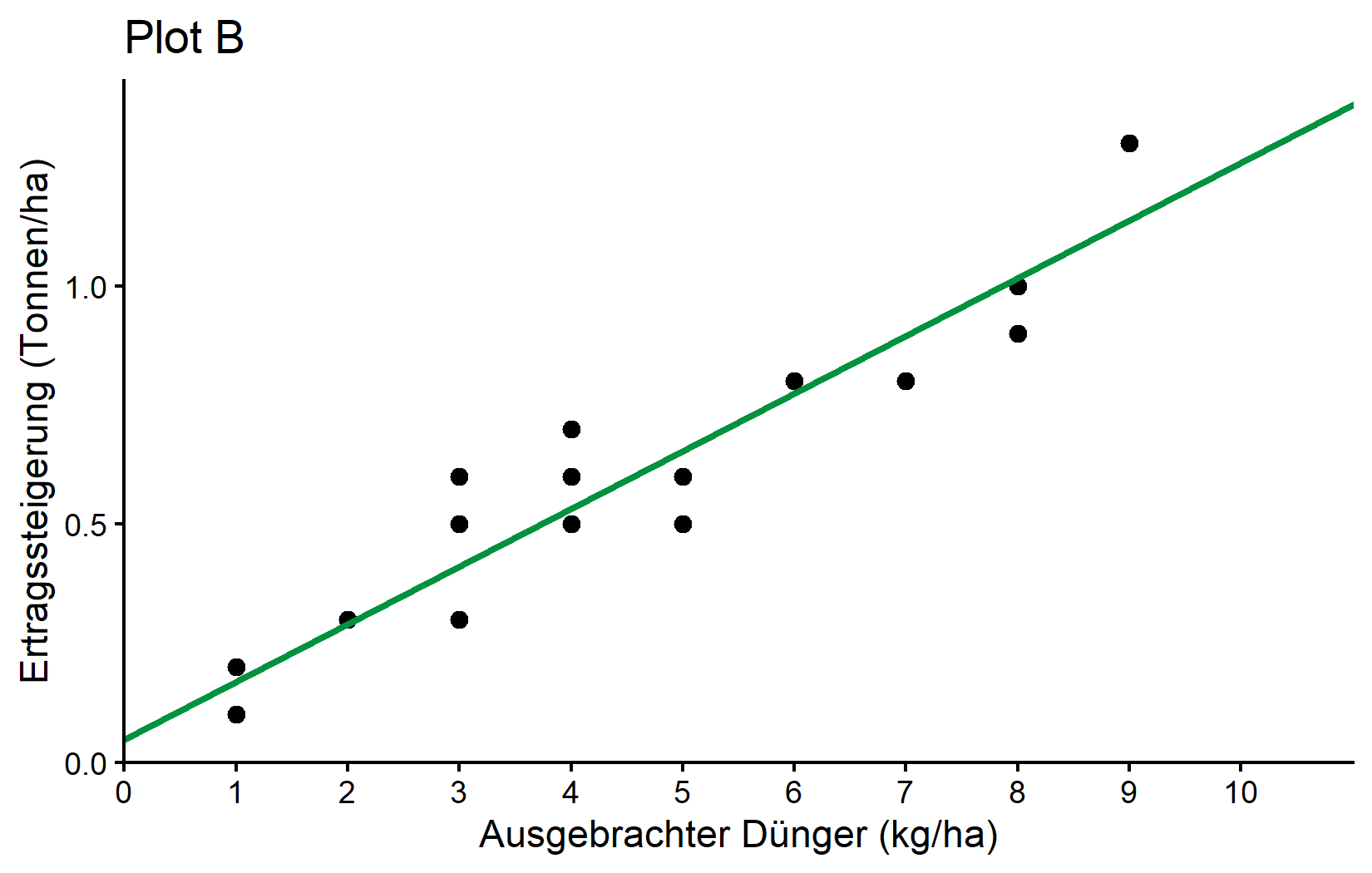
\[ yield\_inc = 0,049 + 0,121 * fert \]
was so aussieht:
Hier ist ein wenig mehr Information darüber, warum formula = yield_inc ~ fert dazu führt, dass R die gewünschten \(a\) und \(b\) schätzt: Was Sinn macht ist, dass yield_inc \(y\) ist, fert ist \(x\) und ~ wäre daher das \(=\) in unserer Gleichung. Aber warum mussten wir nie etwas über \(a\) oder \(b\) schreiben? Die Antwort ist, dass (i) bei der Anpassung eines linearen Modells normalerweise standardmäßig immer ein Achsenabschnitt (=\(a\)) vorhanden ist und (ii) wenn man eine numerische Variable (=fert) auf der rechten Seite der Gleichung schreibt, automatisch angenommen wird, dass sie eine Steigung (=\(b\)) multipliziert mit ihr hat. Dementsprechend übersetzt sich yield_inc ~ fert automatisch zu yield_inc = a + b*fert sozusagen.
Ist das richtig?
Nach der Anpassung eines Modells kann man es verwenden, um Vorhersagen zu treffen. Hier ist eine Möglichkeit, die erwartete Ertragssteigerung für die Ausbringung von 0 bis 10 kg/ha Dünger gemäß unserer einfachen linearen Regression zu erhalten:
preddat <- tibble(fert = seq(0, 10))
preddat %>%
mutate(predicted_yield_inc = predict(reg, newdata = preddat))# A tibble: 11 × 2
fert predicted_yield_inc
<int> <dbl>
1 0 0.0490
2 1 0.170
3 2 0.291
4 3 0.412
5 4 0.533
6 5 0.654
7 6 0.775
8 7 0.896
9 8 1.02
10 9 1.14
11 10 1.26 Man kann bemerken, dass die erwartete Ertragssteigerung bei der Ausbringung von 0 kg/ha Dünger tatsächlich 0,049 Tonnen/ha beträgt und somit größer als 0 ist. Dies ist unerwartet. Wenn kein zusätzlicher Dünger ausgebracht wird, sollte es keine zusätzliche Ernte im Vergleich zu den ungedüngten Kontrollparzellen geben. Was ist also schief gelaufen?
Zunächst einmal werden Daten niemals perfekt sein. Selbst wenn der wahre Wert für etwas 0 ist, wird seine Schätzung basierend auf gemessenen Daten niemals genau 0,000000… sein. Stattdessen gibt es immer “Rauschen” in den Daten, z.B. Messfehler: Die Landwirte haben möglicherweise die genaue Menge des Düngers falsch berechnet oder es könnte Fehler bei der Messung der Ertragssteigerung oder zufällige Umwelteinflüsse usw. geben.
Ich möchte also, dass man über das Problem aus zwei anderen Blickwinkeln nachdenkt:
- Sagen die Ergebnisse wirklich, dass der Achsenabschnitt > 0 ist?
- Haben wir überhaupt die richtige Frage gestellt oder hätten wir ein anderes Modell anpassen sollen?
Sagen die Ergebnisse wirklich, dass der Achsenabschnitt > 0 ist?
Nein, das tun sie nicht. Ja, die Stichprobenschätzung für den Achsenabschnitt ist 0,049, aber wenn man sich detailliertere Informationen über z.B. summary() ansieht, können wir mehr sehen:
summary(reg)
Call:
lm(formula = yield_inc ~ fert, data = dat)
Residuals:
Min 1Q Median 3Q Max
-0.154206 -0.070011 -0.004206 0.039202 0.187891
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.048963 0.040592 1.206 0.243
fert 0.121049 0.008764 13.811 5.09e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1009 on 18 degrees of freedom
Multiple R-squared: 0.9138, Adjusted R-squared: 0.909
F-statistic: 190.8 on 1 and 18 DF, p-value: 5.089e-11Man kann sehen, dass der p-Wert für den Achsenabschnitt größer als 0,05 ist und somit besagt, dass wir den Achsenabschnitt nicht als signifikant von 0 verschieden feststellen konnten (siehe Kapitel “033_tests_and_pvalues” für Details zur Interpretation).
Hätten wir ein anderes Modell anpassen sollen?
Wir hätten das sicherlich können und werden es jetzt tatsächlich tun. Es muss klar sein, dass statistisch gesehen nichts falsch mit unserer Analyse war. Jedoch hätten wir aus agronomischer Sicht oder mit anderen Worten - aufgrund unseres Hintergrundwissens und unserer Expertise als Agrarwissenschaftler - tatsächlich aktiv für eine Regressionsanalyse entscheiden können, die keinen Achsenabschnitt hat und somit gezwungen ist, bei 0 in Bezug auf die Ertragssteigerung zu beginnen. Schließlich ist Statistik nur ein Werkzeug, um uns bei Schlussfolgerungen zu helfen. Es ist ein mächtiges Werkzeug, aber es wird immer unsere Verantwortung bleiben, “die richtigen Fragen zu stellen”, d.h. zweckmäßige Methoden anzuwenden.
Eine einfache lineare Regression ohne Achsenabschnitt ist streng genommen nicht mehr “einfach”, da sie nicht mehr die typische Gleichung hat, sondern stattdessen diese:
\[ y = \beta x\]
Um lm() zu sagen, dass es nicht den standardmäßigen Achsenabschnitt schätzen soll, fügen wir einfach 0 + direkt nach dem ~ hinzu. Wie erwartet erhalten wir nur eine Schätzung für die Steigung:
reg_noint <- lm(formula = yield_inc ~ 0 + fert, data = dat)
reg_noint
Call:
lm(formula = yield_inc ~ 0 + fert, data = dat)
Coefficients:
fert
0.1298 Das bedeutet, dass diese Regression ohne Achsenabschnitt geschätzt wird als
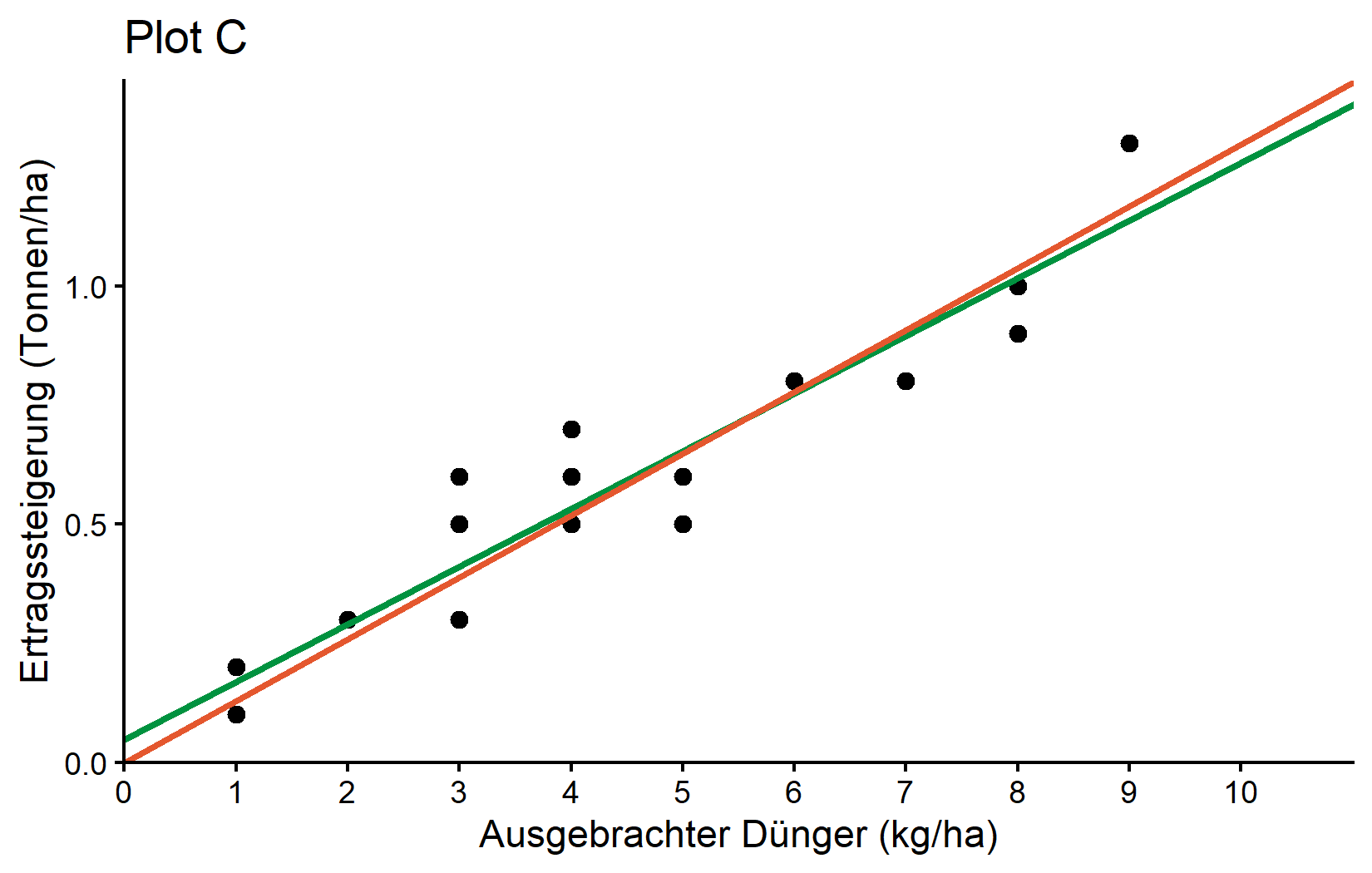
\[ yield\_inc = 0,1298 * fert \]
und definitiv 0 yield_inc vorhersagen muss, wenn 0 kg/ha fert ausgebracht werden. Als Endergebnis können wir beide Regressionslinien visuell in einem ggplot vergleichen:
Schließlich noch ein kleiner Tipp: Das Paket {broom} ist ein sehr nützliches Paket zum Aufräumen der Ausgabe von Modellen oder anderen statistischen Analysen. Es ist nicht eingebaut, daher muss man es zuerst mit install.packages("broom") installieren und mit library(broom) laden. Man kann dann seine drei Funktionen tidy(), glance() und augment() verwenden, um die Ergebnisse der statistischen Analyse in einem “aufgeräumten” Tibble-Format zu erhalten. Dies ist besonders nützlich, wenn das Ziel der Export dieser Ergebnisse ist. Zum Beispiel können wir tidy() sowohl auf unsere Korrelations- als auch auf unsere linearen Regressionsergebnisse anwenden:
library(broom)
tidy(mycor)# A tibble: 1 × 8
estimate statistic p.value parameter conf.low conf.high method alternative
<dbl> <dbl> <dbl> <int> <dbl> <dbl> <chr> <chr>
1 0.956 13.8 5.09e-11 18 0.890 0.983 Pearson'… two.sided tidy(reg)# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.0490 0.0406 1.21 2.43e- 1
2 fert 0.121 0.00876 13.8 5.09e-11Versuche den Code selbst auszuführen und vergleiche dies mit dem einfachen Ausführen von mycor und reg ohne die tidy() Funktion. Eine Liste aller Dinge, die mit dieser Funktion aufgeräumt werden können, findest du hier.
Zusammenfassung
Glückwunsch! Du hast die Grundlagen der Korrelations- und Regressionsanalyse gelernt, zwei der am häufigsten verwendeten statistischen Techniken zur Analyse von Beziehungen zwischen numerischen Variablen in der Agrarforschung.
-
Korrelation misst die Stärke und Richtung einer linearen Beziehung zwischen zwei Variablen:
- Werte reichen von -1 bis 1
- Näher zu 1: Starke positive Korrelation
- Näher zu -1: Starke negative Korrelation
- Nahe 0: Wenig bis keine Korrelation
- Korrelation impliziert keine Kausalität
-
Einfache lineare Regression passt eine gerade Linie an Daten an, um die Beziehung zwischen Variablen zu modellieren:
- Formel: y = α + βx (mit Achsenabschnitt) oder y = βx (ohne Achsenabschnitt)
- Hier gibt die Steigung (β) an, um wie viel der Ertrag zunimmt, wenn die Düngerzufuhr um 1 kg/ha zunimmt
- Hier gibt der Achsenabschnitt (α) die erwartete Ertragssteigerung an, wenn kein Dünger ausgebracht wird
- Ermöglicht Vorhersagen von Ertragssteigerungen basierend auf geplanten Düngeranwendungen
-
Modellbewertung ist entscheidend für die Bestimmung, ob die Regression Sinn macht:
- Prüfe, ob Koeffizienten statistisch signifikant sind
-
Statistische vs. praktische Signifikanz
- Manchmal kann Fachwissen (wie das Wissen, dass die Ertragssteigerung bei null Dünger null sein sollte) Einschränkungen darüber nahelegen, wie das Modell aussehen sollte.
- Vergiss nicht, dass statistische Werkzeuge Leitfäden sind, aber deine Expertise sollte deine endgültige Interpretation und Modellierungsauswahl informieren.
Fußnoten
Die Zahlen für ausgebrachten Dünger in kg/ha und Ertragssteigerung in t/ha sind erfunden und wurden der Einfachheit halber gewählt, anstatt realistisch zu sein.↩︎
Zitat
@online{schmidt2026,
author = {{Dr. Paul Schmidt}},
publisher = {BioMath GmbH},
title = {4. Korrelation \& Regression},
date = {2026-02-07},
url = {https://biomathcontent.netlify.app/de/content/r_intro/04_correlationregression.html},
langid = {de}
}