Um alle in diesem Kapitel verwendeten Pakete zu installieren und zu laden, führe folgenden Code aus:
Von CRD zu RCBD
Im vorherigen Kapitel analysierten wir Daten aus einem Melonensorten-Versuch mit einem vollständig randomisierten Design (CRD). In einem CRD werden Behandlungen zufällig den Versuchseinheiten (Parzellen) ohne Einschränkungen zugeordnet. Obwohl dies das einfachste Design ist, wird angenommen, dass alle Versuchseinheiten gleich variabel sind.
In landwirtschaftlichen Versuchen stehen wir jedoch oft vor Situationen, in denen unsere Versuchseinheiten nicht homogen sind:
- Felder können Gradienten in der Bodenfruchtbarkeit aufweisen
- Gewächshaustische können unterschiedliche Licht- oder Temperaturverhältnisse haben
- Laborarbeiten können sich über mehrere Tage mit unterschiedlichen Bedingungen erstrecken
Warum Blöcke verwenden?
Eine Randomisierte vollständige Blockanlage (RCBD) begegnet dem, indem Versuchseinheiten in “Blöcke” gruppiert werden, wobei Einheiten innerhalb jedes Blocks einander ähnlicher sind als Einheiten in anderen Blöcken. Dann erscheint jede Behandlung genau einmal in jedem Block (daher “vollständige” Blockanlage).
Die Vorteile des Blockens umfassen:
- Erhöhte Präzision: Durch Berücksichtigung bekannter Variationsquellen über die Blöcke reduzieren wir unerklärte Variation (Rauschen/Fehler)
- Bessere Schätzungen: Als Folge werden Behandlungseffekte präziser geschätzt
- Gültige Vergleiche: Jede Behandlung ist denselben Bedingungen über alle Blöcke hinweg ausgesetzt
Man kann es so betrachten: In einem CRD wird alle Variation entweder durch Behandlungen erklärt oder als zufälliger Fehler betrachtet. In einem RCBD wird alle Variation entweder durch Behandlungen oder durch Blöcke erklärt, wodurch weniger unerklärte Variation übrig bleibt.
Daten
Für dieses Beispiel verwenden wir Daten aus einem Sortenversuch von Clewer & Scarisbrick (2001). Das Experiment testete vier Sorten in drei Blöcken. Die Zielvariable ist der Ertrag (t/ha).
Rows: 12 Columns: 5
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (2): block, cultivar
dbl (3): yield, row, col
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.# A tibble: 12 × 5
block cultivar yield row col
<chr> <chr> <dbl> <dbl> <dbl>
1 B1 C1 7.4 2 1
2 B1 C2 9.8 3 1
3 B1 C3 7.3 1 1
4 B1 C4 9.5 4 1
5 B2 C1 6.5 1 2
6 B2 C2 6.8 4 2
7 B2 C3 6.1 3 2
8 B2 C4 8 2 2
9 B3 C1 5.6 2 3
10 B3 C2 6.2 1 3
11 B3 C3 6.4 3 3
12 B3 C4 7.4 4 3Der Datensatz enthält:
-
cultivar: Vier Sorten mit den Bezeichnungen C1 bis C4 -
block: Drei Blöcke mit den Bezeichnungen B1 bis B3 -
yield: Ernteertrag in Tonnen pro Hektar -
rowundcol: Feldparzellenkoordinaten für die Visualisierung mit desplot
Format
Wie bei der vorherigen Analyse müssen wir sicherstellen, dass unsere kategorialen Variablen ordnungsgemäß als Faktoren formatiert sind. Hier bedeutet das die Formatierung von zwei Variablen: block und cultivar. Unten sind zwei verschiedene Wege dafür gezeigt.
# A tibble: 12 × 5
block cultivar yield row col
<fct> <fct> <dbl> <dbl> <dbl>
1 B1 C1 7.4 2 1
2 B1 C2 9.8 3 1
3 B1 C3 7.3 1 1
4 B1 C4 9.5 4 1
5 B2 C1 6.5 1 2
6 B2 C2 6.8 4 2
7 B2 C3 6.1 3 2
8 B2 C4 8 2 2
9 B3 C1 5.6 2 3
10 B3 C2 6.2 1 3
11 B3 C3 6.4 3 3
12 B3 C4 7.4 4 3Erkunden
Schauen wir uns zunächst die zusammenfassenden Statistiken sowohl nach Sorte als auch nach Block an, um die Datenstruktur zu verstehen:
# A tibble: 4 × 6
cultivar count mean_yield sd_yield min_yield max_yield
<fct> <int> <dbl> <dbl> <dbl> <dbl>
1 C4 3 8.3 1.08 7.4 9.5
2 C2 3 7.6 1.93 6.2 9.8
3 C3 3 6.6 0.624 6.1 7.3
4 C1 3 6.5 0.9 5.6 7.4# A tibble: 3 × 6
block count mean_yield sd_yield min_yield max_yield
<fct> <int> <dbl> <dbl> <dbl> <dbl>
1 B1 4 8.5 1.33 7.3 9.8
2 B2 4 6.85 0.819 6.1 8
3 B3 4 6.4 0.748 5.6 7.4Wir sehen, dass:
- Sorte C4 den höchsten mittleren Ertrag hat
- Block B1 deutlich höhere Erträge als B2 und B3 aufweist
Um es klarzustellen: Alles scheint in Block B1 besser zu wachsen. Das ist kein Sorteneffekt - es ist ein Blockeffekt. Es kann nicht an einer Sorte liegen, weil alle Sorten in jedem Block vorhanden sind. Genau deshalb verwenden wir Blöcke - es gibt systematische Unterschiede zwischen Blöcken, die wir berücksichtigen wollen.
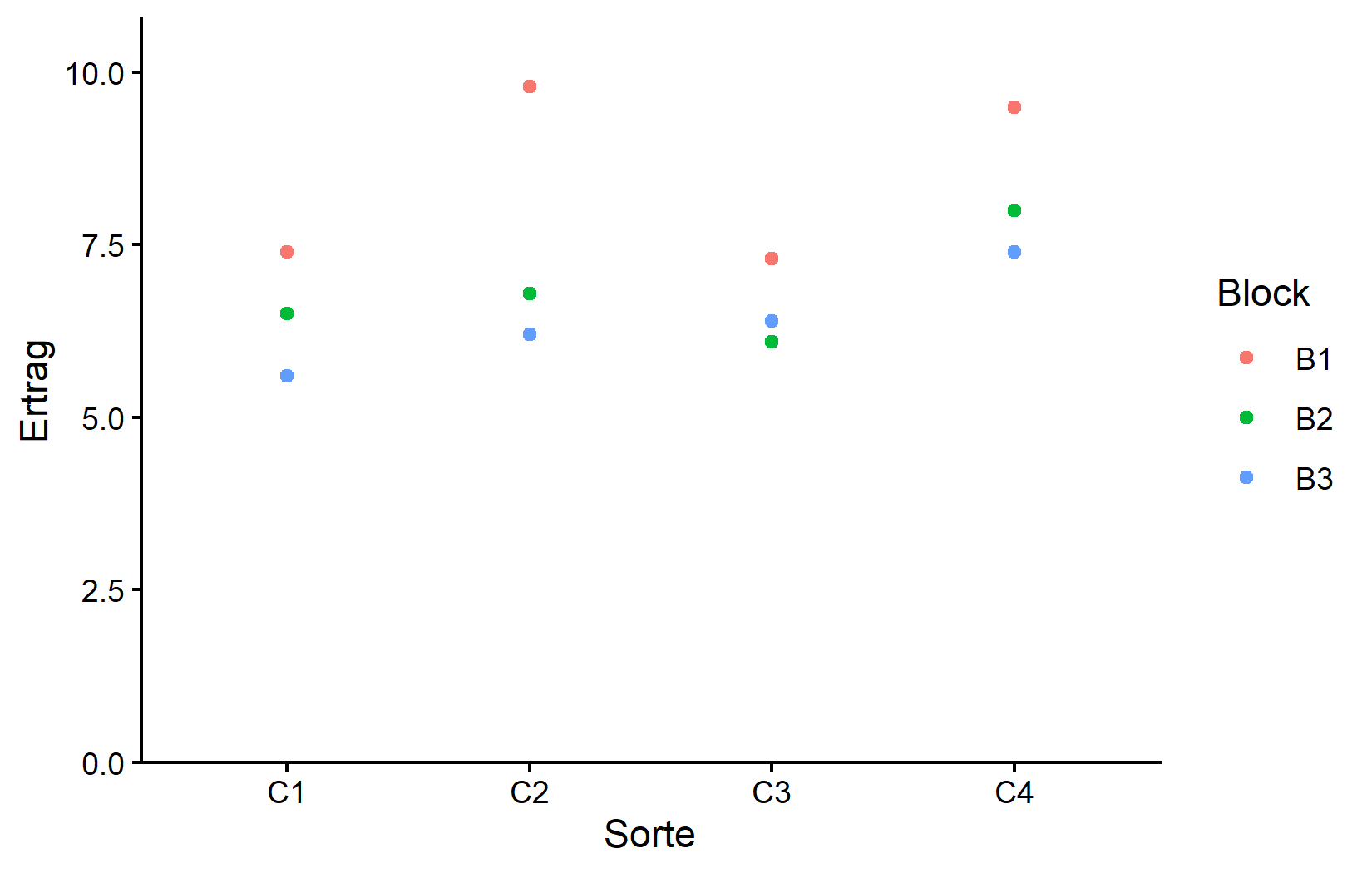
Visualisieren wir die Daten, um die Beziehung zwischen Sorten und Blöcken zu sehen:
ggplot(data = dat) +
aes(y = yield, x = cultivar, color = block) +
geom_point() +
scale_x_discrete(
name = "Sorte"
) +
scale_y_continuous(
name = "Ertrag",
limits = c(0, NA),
expand = expansion(mult = c(0, 0.1))
) +
scale_color_discrete(
name = "Block"
) +
theme_classic()Diese Grafik zeigt, wie sich Erträge sowohl nach Sorte (x-Achse) als auch nach Block (Farbe) unterscheiden. Beachte, dass jede Sorte ihren höchsten Ertrag in Block B1 hatte. Das ist wieder ein klarer Hinweis auf den Blockeffekt. Etwas an Block B1 lässt alles besser wachsen.
Jetzt visualisieren wir die Versuchsanlage, um die räumliche Anordnung zu verstehen:
desplot(
data = dat,
flip = TRUE, # Reihe 1 oben, nicht unten
form = cultivar ~ col + row, # Füllfarbe je Sorte
out1 = block, # Linie zwischen Blöcken
text = cultivar, # Sortennamen je Parzelle
cex = 1, # Sortennamen: Schriftgröße
shorten = FALSE, # Sortennamen: nicht abkürzen
main = "Feld-Layout: Sorten", # Titel der Grafik
show.key = FALSE # Legende ausblenden
)desplot(
data = dat,
flip = TRUE, # Reihe 1 oben, nicht unten
form = yield ~ col + row, # Füllfarbe nach Ertrag
out1 = block, # Linie zwischen Blöcken
text = cultivar, # Sortennamen je Parzelle
cex = 1, # Sortennamen: Schriftgröße
shorten = FALSE, # Sortennamen: nicht abkürzen
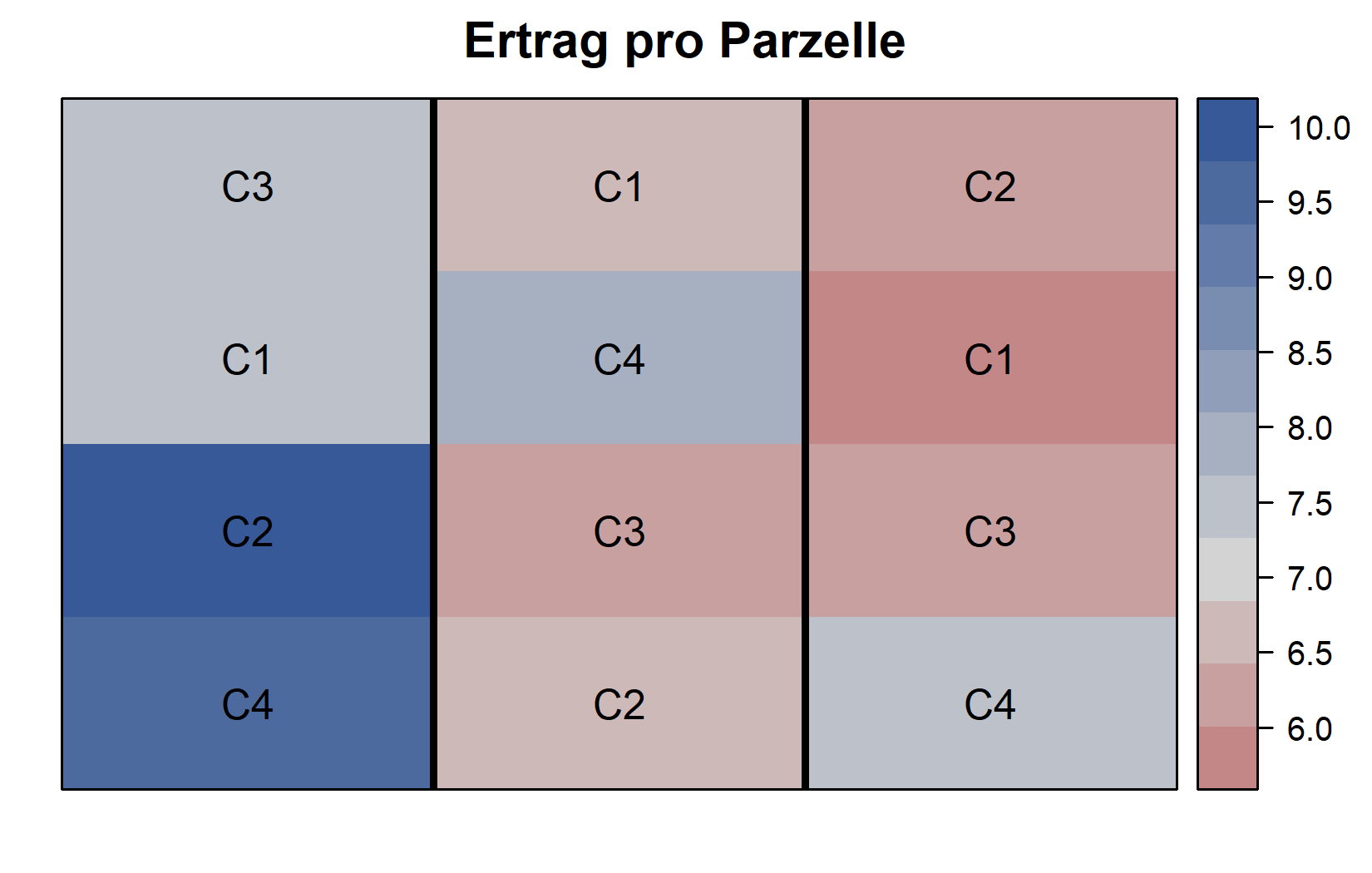
main = "Ertrag pro Parzelle", # Titel der Grafik
show.key = FALSE # Legende ausblenden
)Die Feld-Layouts bestätigen:
- Jede Sorte erscheint genau einmal in jedem Block (vollständige Blockanlage)
- Block B1 (links) hat generell höhere Erträge als die anderen Blöcke
- Innerhalb jedes Blocks hat Sorte C4 entweder den höchsten oder zweithöchsten Ertrag verglichen mit den anderen Sorten
Modell und ANOVA
Das RCBD-Modell verstehen
Der Hauptunterschied zwischen CRD und RCBD in Bezug auf die Modellformulierung ist ein zusätzlicher Effekt für Blöcke. In einem CRD schließen wir nur den Behandlungseffekt ein:
yield ~ cultivar
In einem RCBD fügen wir den Blockeffekt hinzu:
yield ~ cultivar + block
Fitten wir dieses Modell:
mod <- lm(yield ~ cultivar + block, data = dat)
mod
Call:
lm(formula = yield ~ cultivar + block, data = dat)
Coefficients:
(Intercept) cultivarC2 cultivarC3 cultivarC4 blockB2 blockB3
7.75 1.10 0.10 1.80 -1.65 -2.10 Beachte, dass die Koeffizienten jetzt sowohl Sorten- als auch Blockeffekte einschließen und beide wieder ihre erste Stufe “vermissen”. Die Blockeffekte (blockB2 und blockB3) sind beide negativ, was niedrigere Erträge in diesen Blöcken verglichen mit Block B1 (der als Referenzstufe auf 0 gesetzt ist) anzeigt. Die Sorteneffekte (cultivarC2, cultivarC3 und cultivarC4) sind alle positiv, was höhere Erträge verglichen mit Sorte C1 (der als Referenzstufe auf 0 gesetzt ist) anzeigt. Das ist jedoch Zufall, da diese Stufen nicht in einer bestimmten Reihenfolge sortiert sind und es immer die erste Stufe ist, die auf 0 gesetzt wird.
Die gute Nachricht ist, dass ab hier alles gleich wie bei der CRD-Analyse ist. Wir können immer noch die anova()-Funktion verwenden, um eine ANOVA auf diesem Modell durchzuführen, und wir können immer noch emmeans() verwenden, um geschätzte Randmittel (adjustierte Mittel) für unsere Sorten zu erhalten. Abgesehen davon, dass unser Faktor cultivar statt variety heißt, müssen wir nicht einmal den Code aus dem vorherigen Kapitel ändern. Die wichtige Änderung ist, dass wir jetzt den Blockeffekt in unser Modell einbezogen haben. Die ANOVA-Tabelle wird daher auch den Blockeffekt enthalten. Die adjustierten Mittel - oder vielmehr ihre Standardfehler - werden auch für den Blockeffekt adjustiert.
An dieser Stelle (d.h. nach dem Modell-Fit und vor der ANOVA-Interpretation) sollte man prüfen, ob die Modellannahmen erfüllt sind. Mehr dazu im Anhang A1: Modelldiagnostik.
Durchführung der ANOVA
ANOVA <- anova(mod)
ANOVAAnalysis of Variance Table
Response: yield
Df Sum Sq Mean Sq F value Pr(>F)
cultivar 3 6.63 2.21 5.525 0.036730 *
block 2 9.78 4.89 12.225 0.007651 **
Residuals 6 2.40 0.40
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1In dieser ANOVA-Tabelle:
- Beide Effekte erscheinen in der Tabelle:
cultivarundblock - Sowohl Sorten- (p < 0.05) als auch Blockeffekte (p < 0.05) sind statistisch signifikant
Dass der Blockeffekt statistisch signifikant ist, bestätigt, dass das Blocken vorteilhaft war - wir verwerfen die Nullhypothese, dass es keinen Unterschied zwischen Blöcken gibt. Indem wir also den Blockeffekt in unser Modell einbezogen haben, haben wir diese Variation berücksichtigt, die andernfalls dem Fehler/unerklärten Rauschen zugeschrieben worden wäre. Obwohl wir uns hauptsächlich für Sorteneffekte interessieren, verbessert die Einbeziehung des Blockeffekts unsere Analyse.
Dass der Sorteneffekt statistisch signifikant ist, zeigt an, dass sich mindestens eine Sorte von den anderen unterscheidet. Das ist natürlich unser Hauptinteresse. Wir können nun zu Post-hoc-Vergleichen übergehen, um zu identifizieren, welche Sorten sich signifikant voneinander unterscheiden.
Mittelwertvergleiche
Wie in der CRD-Analyse verwenden wir geschätzte Randmittel (emmeans) für Post-hoc-Vergleiche:
cultivar emmean SE df lower.CL upper.CL .group
C1 6.5 0.365 6 5.61 7.39 a
C3 6.6 0.365 6 5.71 7.49 a
C2 7.6 0.365 6 6.71 8.49 ab
C4 8.3 0.365 6 7.41 9.19 b
Results are averaged over the levels of: block
Confidence level used: 0.95
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Beachte, dass diese Mittel für Blockeffekte adjustiert sind. In einem balancierten Design wie diesem (jede Sorte erscheint einmal in jedem Block) sind die adjustierten Mittel die Sortendurchschnitte über Blöcke hinweg. Der emmeans-Ansatz berücksichtigt die Blockstruktur bei der Berechnung der Standardfehler.
Ergebnisse visualisieren
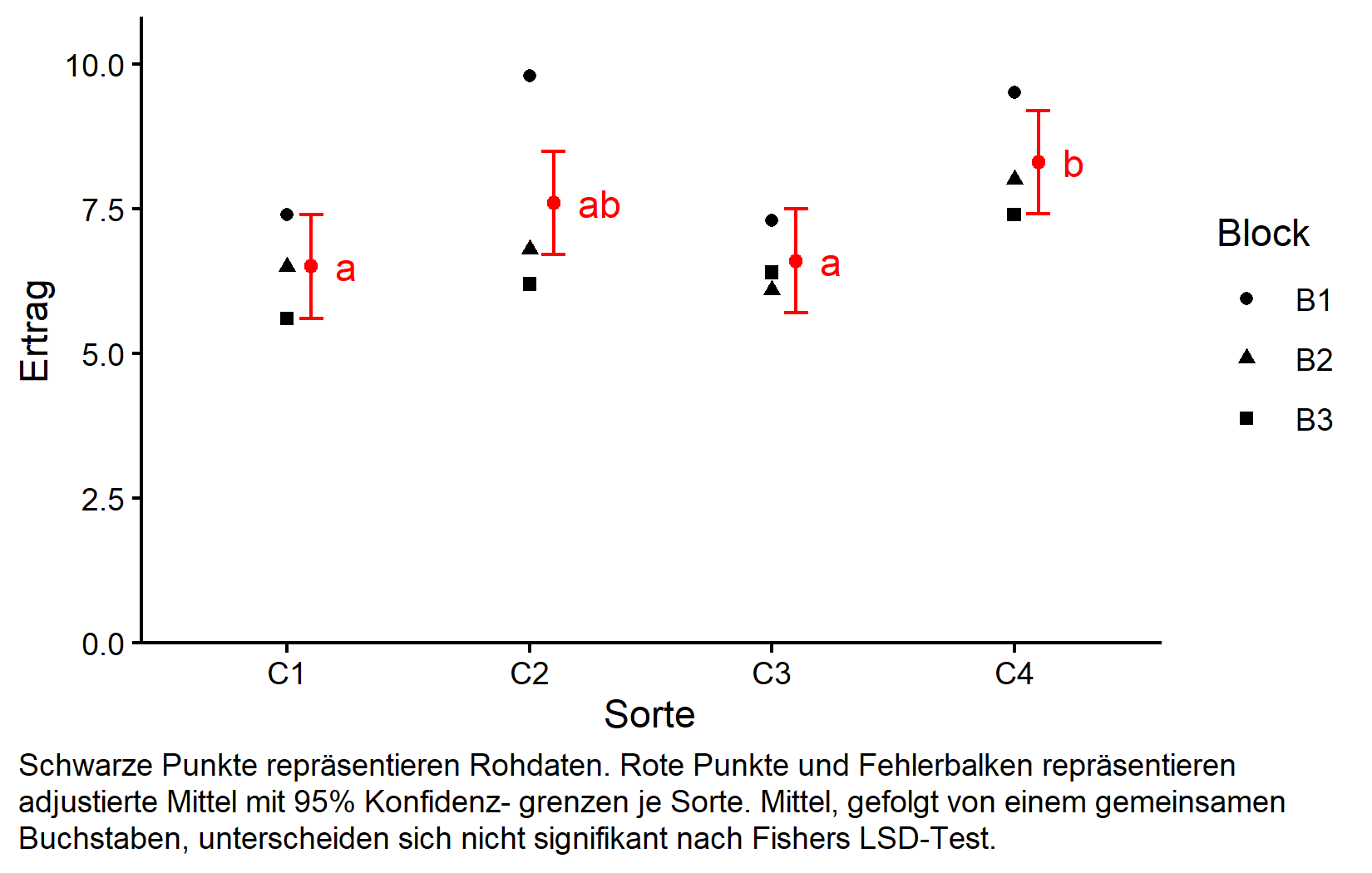
Als abschließender Schritt in diesem Material erstellen wir eine umfassende Grafik, die sowohl die Rohdaten als auch die statistischen Ergebnisse zeigt. Um jede Komponente der Grafik zu verstehen, schaue bitte das Video zu diesem Kapitel an.
my_caption <- "Schwarze Punkte repräsentieren Rohdaten.
Rote Punkte und Fehlerbalken repräsentieren adjustierte Mittel mit 95% Konfidenz-
grenzen je Sorte. Mittel, gefolgt von einem gemeinsamen Buchstaben, unterscheiden
sich nicht signifikant nach Fishers LSD-Test."
ggplot() +
aes(x = cultivar) +
# schwarze Punkte für die Rohdaten
geom_point(
data = dat,
aes(y = yield, shape = block)
) +
# rote Punkte für die adjustierten Mittel
geom_point(
data = mean_comp,
aes(y = emmean),
color = "red",
position = position_nudge(x = 0.1)
) +
# rote Fehlerbalken für die Konfidenzgrenzen der adjustierten Mittel
geom_errorbar(
data = mean_comp,
aes(ymin = lower.CL, ymax = upper.CL),
color = "red",
width = 0.1,
position = position_nudge(x = 0.1)
) +
# rote Buchstaben
geom_text(
data = mean_comp,
aes(y = emmean, label = str_trim(.group)),
color = "red",
position = position_nudge(x = 0.2),
hjust = 0
) +
scale_x_discrete(
name = "Sorte"
) +
scale_y_continuous(
name = "Ertrag",
limits = c(0, NA),
expand = expansion(mult = c(0, 0.1))
) +
scale_shape_discrete(
name = "Block"
) +
theme_classic() +
labs(caption = my_caption) +
theme(plot.caption = element_textbox_simple(margin = margin(t = 5)),
plot.caption.position = "plot")CRD vs RCBD Vergleich
Fassen wir die wichtigsten Unterschiede zwischen unseren CRD- und RCBD-Analysen zusammen:
-
Modellformel:
- CRD:
yield ~ cultivar - RCBD:
yield ~ cultivar + block
- CRD:
-
Variationsquellen:
- CRD: Behandlung und Residualfehler
- RCBD: Behandlung, Blöcke und Residualfehler
-
Präzision:
- CRD: Alle unerklärte Variation geht in den Fehler
- RCBD: Blockvariation wird vom Fehler entfernt, erhöht die Präzision
-
Wann verwenden:
- CRD: Wenn Versuchseinheiten homogen sind
- RCBD: Wenn es bekannte Quellen der Heterogenität gibt
Abschluss
Du hast nun gelernt, wie man Daten aus einer randomisierten vollständigen Blockanlage analysiert und dabei auf den Konzepten aus der vollständig randomisierten Anlage aufbaust. Blocken ist ein mächtiges Werkzeug, das die Präzision deiner Versuche erhöht, wenn man mit heterogenen Versuchsbedingungen umgeht.
Randomisierte vollständige Blockanlage (RCBD) gruppiert ähnliche Versuchseinheiten in Blöcke und reduziert unerklärte Variation.
Blocken verbessert die Präzision durch Berücksichtigung bekannter Variationsquellen und macht Behandlungsvergleiche genauer.
Das RCBD-Modell schließt sowohl Behandlungs- als auch Blockeffekte ein:
response ~ treatment + block.ANOVA für RCBD testet sowohl Behandlungs- als auch Blockeffekte, obwohl wir uns hauptsächlich für Behandlungen interessieren.
Geschätzte Randmittel in RCBD sind für Blockeffekte adjustiert und bieten bessere Behandlungsvergleiche.
Damit schließt unsere Einführung in die Analyse von Versuchsanlagen ab. Du hast nun die Werkzeuge, um sowohl einfache (CRD) als auch komplexere (RCBD) Versuchsanlagen mit ANOVA und Mittelwertvergleichstechniken in R zu handhaben.
Zitat
@online{schmidt2026,
author = {{Dr. Paul Schmidt}},
publisher = {BioMath GmbH},
title = {2. Einfaktorielle ANOVA in einem RCBD},
date = {2026-02-08},
url = {https://biomathcontent.netlify.app/de/content/lin_mod_exp/02_oneway_rcbd.html},
langid = {de}
}